我们通常所说的堆是指二叉堆,二叉堆又称完全二叉树或者叫近似完全二叉树。二叉堆又分为最大堆和最小堆。
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法,它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。数组可以根据索引直接获取元素,时间复杂度为O(1),也就是常量,因此对于取值效率极高。
这里以最大堆为例:
最大堆的特性如下:
父结点的键值总是大于或者等于任何一个子节点的键值
每个结点的左子树和右子树都是一个最大堆
最大堆的算法思想是:
先将初始的R[0…n-1]建立成最大堆,此时是无序堆,而堆顶是最大元素
再将堆顶R[0]和无序区的最后一个记录R[n-1]交换,由此得到新的无序区R[0…n-2]和有序区R[n-1],且满足R[0…n-2].keys ≤ R[n-1].key
由于交换后,前R[0…n-2]可能不满足最大堆的性质,因此再调整前R[0…n-2]为最大堆,直到只有R[0]最后一个元素才调整完成。
最大堆排序完成后,其实是升序序列,每次调整堆都是要得到最大的一个元素,然后与当前堆的最后一个元素交换,因此最后所得到的序列是升序序列。
构建堆:
1 #ifndef INC_06_HEAP_SORT_HEAP_H 2 #define INC_06_HEAP_SORT_HEAP_H 3 #include <algorithm> 4 #include <cassert> 5 using namespace std; 6 template<typename Item> 7 class MaxHeap{ 8 private: 9 Item *data; 10 int count; 11 int capacity; 12 13 void shiftUp(int k){ 14 while( k > 1 && data[k/2] < data[k] ){ 15 swap( data[k/2], data[k] ); 16 k /= 2; 17 } 18 } 19 20 void shiftDown(int k){ 21 while( 2*k <= count ){ 22 int j = 2*k; 23 if( j+1 <= count && data[j+1] > data[j] ) j ++; 24 if( data[k] >= data[j] ) break; 25 swap( data[k] , data[j] ); 26 k = j; 27 } 28 } 29 30 public: 31 32 // 构造函数, 构造一个空堆, 可容纳capacity个元素 33 MaxHeap(int capacity){ 34 data = new Item[capacity+1]; 35 count = 0; 36 this->capacity = capacity; 37 } 38 // 构造函数, 通过一个给定数组创建一个最大堆 39 // 该构造堆的过程, 时间复杂度为O(n) 40 MaxHeap(Item arr[], int n){ 41 data = new Item[n+1]; 42 capacity = n; 43 for( int i = 0 ; i < n ; i ++ ) 44 data[i+1] = arr[i]; 45 count = n; 46 47 for( int i = count/2 ; i >= 1 ; i -- ) 48 shiftDown(i); 49 } 50 ~MaxHeap(){ 51 delete[] data; 52 } 53 54 // 返回堆中的元素个数 55 int size(){ 56 return count; 57 } 58 59 // 返回一个布尔值, 表示堆中是否为空 60 bool isEmpty(){ 61 return count == 0; 62 } 63 64 // 像最大堆中插入一个新的元素 item 65 void insert(Item item){ 66 assert( count + 1 <= capacity ); 67 data[count+1] = item; 68 shiftUp(count+1); 69 count ++; 70 } 71 72 // 从最大堆中取出堆顶元素, 即堆中所存储的最大数据 73 Item extractMax(){ 74 assert( count > 0 ); 75 Item ret = data[1]; 76 swap( data[1] , data[count] ); 77 count --; 78 shiftDown(1); 79 return ret; 80 } 81 82 // 获取最大堆中的堆顶元素 83 Item getMax(){ 84 assert( count > 0 ); 85 return data[1]; 86 } 87 }; 88 89 #endif
简单堆排序:
1 #ifndef INC_06_HEAP_SORT_HEAPSORT_H 2 #define INC_06_HEAP_SORT_HEAPSORT_H 3 #include "Heap.h" 4 using namespace std; 5 // heapSort1, 将所有的元素依次添加到堆中, 在将所有元素从堆中依次取出来, 即完成了排序 6 // 无论是创建堆的过程, 还是从堆中依次取出元素的过程, 时间复杂度均为O(nlogn) 7 // 整个堆排序的整体时间复杂度为O(nlogn) 8 template<typename T> 9 void heapSort1(T arr[], int n){ 10 11 MaxHeap<T> maxheap = MaxHeap<T>(n); 12 for( int i = 0 ; i < n ; i ++ ) 13 maxheap.insert(arr[i]); 14 15 for( int i = n-1 ; i >= 0 ; i-- ) 16 arr[i] = maxheap.extractMax(); 17 } 18 // heapSort2, 借助我们的heapify过程创建堆 19 // 此时, 创建堆的过程时间复杂度为O(n), 将所有元素依次从堆中取出来, 实践复杂度为O(nlogn) 20 // 堆排序的总体时间复杂度依然是O(nlogn), 但是比上述heapSort1性能更优, 因为创建堆的性能更优 21 template<typename T> 22 void heapSort2(T arr[], int n){ 23 24 MaxHeap<T> maxheap = MaxHeap<T>(arr,n); 25 for( int i = n-1 ; i >= 0 ; i-- ) 26 arr[i] = maxheap.extractMax(); 27 } 28 #endif
插入排序:
1 #ifndef INC_06_HEAP_SORT_INSERTIONSORT_H 2 #define INC_06_HEAP_SORT_INSERTIONSORT_H 3 #include <iostream> 4 #include <algorithm> 5 using namespace std; 6 template<typename T> 7 void insertionSort(T arr[], int n){ 8 9 for( int i = 1 ; i < n ; i ++ ) { 10 11 T e = arr[i]; 12 int j; 13 for (j = i; j > 0 && arr[j-1] > e; j--) 14 arr[j] = arr[j-1]; 15 arr[j] = e; 16 } 17 18 return; 19 } 20 21 // 对arr[l...r]范围的数组进行插入排序 22 template<typename T> 23 void insertionSort(T arr[], int l, int r){ 24 25 for( int i = l+1 ; i <= r ; i ++ ) { 26 27 T e = arr[i]; 28 int j; 29 for (j = i; j > l && arr[j-1] > e; j--) 30 arr[j] = arr[j-1]; 31 arr[j] = e; 32 } 33 34 return; 35 } 36 37 #endif
归并排序:
1 #ifndef INC_06_HEAP_SORT_MERGESORT_H 2 #define INC_06_HEAP_SORT_MERGESORT_H 3 4 #include <iostream> 5 #include <algorithm> 6 #include "InsertionSort.h" 7 8 using namespace std; 9 10 11 // 将arr[l...mid]和arr[mid+1...r]两部分进行归并 12 // 其中aux为完成merge过程所需要的辅助空间 13 template<typename T> 14 void __merge(T arr[], T aux[], int l, int mid, int r){ 15 16 // 由于aux的大小和arr一样, 所以我们也不需要处理aux索引的偏移量 17 // 进一步节省了计算量:) 18 for( int i = l ; i <= r; i ++ ) 19 aux[i] = arr[i]; 20 21 // 初始化,i指向左半部分的起始索引位置l;j指向右半部分起始索引位置mid+1 22 int i = l, j = mid+1; 23 for( int k = l ; k <= r; k ++ ){ 24 25 if( i > mid ){ // 如果左半部分元素已经全部处理完毕 26 arr[k] = aux[j]; j ++; 27 } 28 else if( j > r ){ // 如果右半部分元素已经全部处理完毕 29 arr[k] = aux[i]; i ++; 30 } 31 else if( aux[i] < aux[j] ) { // 左半部分所指元素 < 右半部分所指元素 32 arr[k] = aux[i]; i ++; 33 } 34 else{ // 左半部分所指元素 >= 右半部分所指元素 35 arr[k] = aux[j]; j ++; 36 } 37 } 38 39 } 40 41 // 使用优化的归并排序算法, 对arr[l...r]的范围进行排序 42 // 其中aux为完成merge过程所需要的辅助空间 43 template<typename T> 44 void __mergeSort(T arr[], T aux[], int l, int r){ 45 46 // 对于小规模数组, 使用插入排序 47 if( r - l <= 15 ){ 48 insertionSort(arr, l, r); 49 return; 50 } 51 52 int mid = (l+r)/2; 53 __mergeSort(arr, aux, l, mid); 54 __mergeSort(arr, aux, mid+1, r); 55 56 // 对于arr[mid] <= arr[mid+1]的情况,不进行merge 57 // 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失 58 if( arr[mid] > arr[mid+1] ) 59 __merge(arr, aux, l, mid, r); 60 } 61 62 63 template<typename T> 64 void mergeSort(T arr[], int n){ 65 66 // 在 mergeSort中, 我们一次性申请aux空间, 67 // 并将这个辅助空间以参数形式传递给完成归并排序的各个子函数 68 T *aux = new T[n]; 69 70 __mergeSort( arr , aux, 0 , n-1 ); 71 72 delete[] aux; // 使用C++, new出来的空间不要忘记释放掉:) 73 } 74 75 #endif
单路快排:
1 #ifndef INC_06_HEAP_SORT_QUICKSORT_H 2 #define INC_06_HEAP_SORT_QUICKSORT_H 3 4 #include <iostream> 5 #include <ctime> 6 #include <algorithm> 7 #include "InsertionSort.h" 8 using namespace std; 9 // 对arr[l...r]部分进行partition操作 10 // 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p] 11 template <typename T> 12 int _partition(T arr[], int l, int r){ 13 14 // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot 15 swap( arr[l] , arr[rand()%(r-l+1)+l] ); 16 17 T v = arr[l]; 18 int j = l; 19 for( int i = l + 1 ; i <= r ; i ++ ) 20 if( arr[i] < v ){ 21 j ++; 22 swap( arr[j] , arr[i] ); 23 } 24 25 swap( arr[l] , arr[j]); 26 27 return j; 28 } 29 30 // 对arr[l...r]部分进行快速排序 31 template <typename T> 32 void _quickSort(T arr[], int l, int r){ 33 34 // 对于小规模数组, 使用插入排序进行优化 35 if( r - l <= 15 ){ 36 insertionSort(arr,l,r); 37 return; 38 } 39 40 int p = _partition(arr, l, r); 41 _quickSort(arr, l, p-1 ); 42 _quickSort(arr, p+1, r); 43 } 44 45 template <typename T> 46 void quickSort(T arr[], int n){ 47 48 srand(time(NULL)); 49 _quickSort(arr, 0, n-1); 50 } 51 52 #endif
双路快排:
1 #ifndef INC_06_HEAP_SORT_QUICKSORT2WAYS_H 2 #define INC_06_HEAP_SORT_QUICKSORT2WAYS_H 3 4 #include <iostream> 5 #include <algorithm> 6 #include "InsertionSort.h" 7 8 using namespace std; 9 10 // 双路快速排序的partition 11 // 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p] 12 template <typename T> 13 int _partition2(T arr[], int l, int r){ 14 15 // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot 16 swap( arr[l] , arr[rand()%(r-l+1)+l] ); 17 T v = arr[l]; 18 19 // arr[l+1...i) <= v; arr(j...r] >= v 20 int i = l+1, j = r; 21 while( true ){ 22 // 注意这里的边界, arr[i] < v, 不能是arr[i] <= v 23 24 while( i <= r && arr[i] < v ) 25 i ++; 26 27 // 注意这里的边界, arr[j] > v, 不能是arr[j] >= v 28 29 while( j >= l+1 && arr[j] > v ) 30 j --; 31 32 34 35 if( i > j ) 36 break; 37 38 swap( arr[i] , arr[j] ); 39 i ++; 40 j --; 41 } 42 43 swap( arr[l] , arr[j]); 44 45 return j; 46 } 47 48 // 对arr[l...r]部分进行快速排序 49 template <typename T> 50 void _quickSort2Ways(T arr[], int l, int r){ 51 52 // 对于小规模数组, 使用插入排序进行优化 53 if( r - l <= 15 ){ 54 insertionSort(arr,l,r); 55 return; 56 } 57 58 // 调用双路快速排序的partition 59 int p = _partition2(arr, l, r); 60 _quickSort2Ways(arr, l, p-1 ); 61 _quickSort2Ways(arr, p+1, r); 62 } 63 64 template <typename T> 65 void quickSort2Ways(T arr[], int n){ 66 67 srand(time(NULL)); 68 _quickSort2Ways(arr, 0, n-1); 69 } 70 71 #endif
三路快排:
1 #ifndef INC_06_HEAP_SORT_QUICKSORT3WAYS_H 2 #define INC_06_HEAP_SORT_QUICKSORT3WAYS_H 3 4 #include <iostream> 5 #include <algorithm> 6 #include "InsertionSort.h" 7 8 using namespace std; 9 10 // 递归的三路快速排序算法 11 template <typename T> 12 void __quickSort3Ways(T arr[], int l, int r){ 13 14 // 对于小规模数组, 使用插入排序进行优化 15 if( r - l <= 15 ){ 16 insertionSort(arr,l,r); 17 return; 18 } 19 20 // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot 21 swap( arr[l], arr[rand()%(r-l+1)+l ] ); 22 23 T v = arr[l]; 24 25 int lt = l; // arr[l+1...lt] < v 26 int gt = r + 1; // arr[gt...r] > v 27 int i = l+1; // arr[lt+1...i) == v 28 while( i < gt ){ 29 if( arr[i] < v ){ 30 swap( arr[i], arr[lt+1]); 31 i ++; 32 lt ++; 33 } 34 else if( arr[i] > v ){ 35 swap( arr[i], arr[gt-1]); 36 gt --; 37 } 38 else{ // arr[i] == v 39 i ++; 40 } 41 } 42 43 swap( arr[l] , arr[lt] ); 44 45 __quickSort3Ways(arr, l, lt-1); 46 __quickSort3Ways(arr, gt, r); 47 } 48 49 template <typename T> 50 void quickSort3Ways(T arr[], int n){ 51 52 srand(time(NULL)); 53 __quickSort3Ways( arr, 0, n-1); 54 } 55 56 #endif
测试用例:
1 #ifndef INC_06_HEAP_SORT_SORTTESTHELPER_H 2 #define INC_06_HEAP_SORT_SORTTESTHELPER_H 3 #include <iostream> 4 #include <algorithm> 5 #include <string> 6 #include <ctime> 7 #include <cassert> 8 #include <string> 9 using namespace std; 10 namespace SortTestHelper { 11 // 生成有n个元素的随机数组,每个元素的随机范围为[rangeL, rangeR] 12 int *generateRandomArray(int n, int range_l, int range_r) { 13 int *arr = new int[n]; 14 srand(time(NULL)); 15 for (int i = 0; i < n; i++) 16 arr[i] = rand() % (range_r - range_l + 1) + range_l; 17 return arr; 18 } 19 // 生成一个近乎有序的数组 20 // 首先生成一个含有[0...n-1]的完全有序数组, 之后随机交换swapTimes对数据 21 // swapTimes定义了数组的无序程度 22 int *generateNearlyOrderedArray(int n, int swapTimes){ 23 int *arr = new int[n]; 24 for(int i = 0 ; i < n ; i ++ ) 25 arr[i] = i; 26 27 srand(time(NULL)); 28 for( int i = 0 ; i < swapTimes ; i ++ ){ 29 int posx = rand()%n; 30 int posy = rand()%n; 31 swap( arr[posx] , arr[posy] ); 32 } 33 34 return arr; 35 } 36 37 // 拷贝整型数组a中的所有元素到一个新的数组, 并返回新的数组 38 int *copyIntArray(int a[], int n){ 39 40 int *arr = new int[n]; 41 //* 在VS中, copy函数被认为是不安全的, 请大家手动写一遍for循环:) 42 copy(a, a+n, arr); 43 return arr; 44 } 45 46 // 打印arr数组的所有内容 47 template<typename T> 48 void printArray(T arr[], int n) { 49 50 for (int i = 0; i < n; i++) 51 cout << arr[i] << " "; 52 cout << endl; 53 54 return; 55 } 56 57 // 判断arr数组是否有序 58 template<typename T> 59 bool isSorted(T arr[], int n) { 60 61 for (int i = 0; i < n - 1; i++) 62 if (arr[i] > arr[i + 1]) 63 return false; 64 65 return true; 66 } 67 68 // 测试sort排序算法排序arr数组所得到结果的正确性和算法运行时间 69 // 将算法的运行时间打印在控制台上 70 template<typename T> 71 void testSort(const string &sortName, void (*sort)(T[], int), T arr[], int n) { 72 73 clock_t startTime = clock(); 74 sort(arr, n); 75 clock_t endTime = clock(); 76 cout << sortName << " : " << double(endTime - startTime) / CLOCKS_PER_SEC << " s"<<endl; 77 78 assert(isSorted(arr, n)); 79 80 return; 81 } 82 83 // 测试sort排序算法排序arr数组所得到结果的正确性和算法运行时间 84 // 将算法的运行时间以double类型返回, 单位为秒(s) 85 template<typename T> 86 double testSort(void (*sort)(T[], int), T arr[], int n) { 87 88 clock_t startTime = clock(); 89 sort(arr, n); 90 clock_t endTime = clock(); 91 92 assert(isSorted(arr, n)); 93 94 return double(endTime - startTime) / CLOCKS_PER_SEC; 95 } 96 97 }; 98 99 #endif
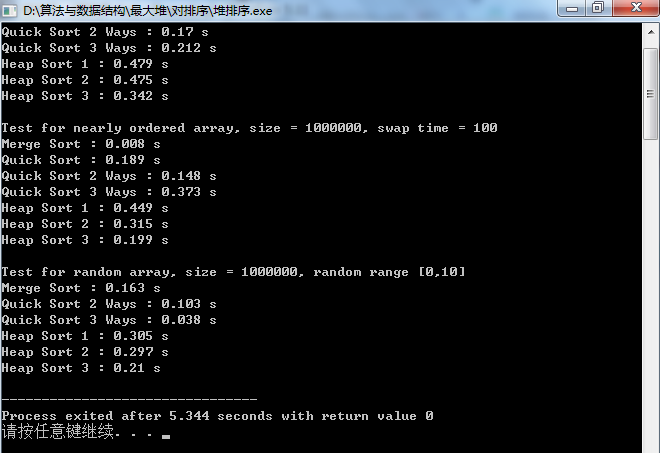
测试结果:
| 平均时间复杂度 | 是否是原地排序 | 需要额外空间 | 稳定排序 | |
| 插入排序 | O(n^2) | 是 | O(1) | 是 |
| 归并排序 | O(nlogn) | 否 | O(n) | 是 |
| 快速排序 | O(nlogn) | 是 | O(logn) | 否 |
| 堆排序 | O(nlogn) | 是 | O(1) | 否 |
稳定性解释:排序后的元素相同元素的顺序依然是排序之前的顺序。
堆排序的最坏时间复杂度为O(N*logN),其平均性能较接近于最坏性能。由于初始建堆所需比较的次数较多,所以堆排序不适合记录数较少的文件,其空间复杂度是O(1),它是一种不稳定的排序算法.