20162307 实验四 图的实现与应用
北京电子科技学院(BESTI)
实 验 报 告
课程:程序设计与数据结构
班级:1623
姓名:张韵琪
学号:20162307
指导教师:娄嘉鹏老师、王志强老师
实验日期:2017年11月15号
实验密级:非密级
实验时间:五天
必修/选修:必修
实验名称:图的实现与应用
实验仪器:电脑
实验目的与要求:
-
目的:
学习查找与排序的应用,实现和分析 -
要求:
1.没有Linux基础的同学建议先学习《Linux基础入门(新版)》《Vim编辑器》 课程
2.完成实验、撰写实验报告,实验报告以博客方式发表在博客园,注意实验报告重点是运行结果,遇到的问题(工具查找,安装,使用,程序的编辑,调试,运行等)、解决办法(空洞的方法如“查网络”、“问同学”、“看书”等一律得0分)以及分析(从中可以得到什么启示,有什么收获,教训等)。报告可以参考范飞龙老师的指导
3. 严禁抄袭,有该行为者实验成绩归零,并附加其他惩罚措施。
实验内容、步骤
一、实验要求
用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
给出伪代码,产品代码,测试代码(不少于5条测试)
一、实验步骤
- 1.邻接矩阵
边的存储方案沿袭于树的树组实现方式,将一维数组替换为二维数组,这里称为邻接矩阵
- 2.无向图
在无向图中,边是双向的。
- 3.用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法
public AbstractGraph() {
//初始化矩阵,一维数组,和边的数目
int n = 0;
edges = new int[n][n];
vertexList = new ArrayList ( n );
numOfEdges = 0;
}
//得到结点的个数
public int getNumOfVertex() {
return vertexList.size ();
}
//得到边的数目
public int getNumOfEdges() {
return numOfEdges;
}
//返回结点i的数据
public Object getValueByIndex(int i) {
return vertexList.get ( i );
}
//返回v1,v2的权值
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
//插入结点
public void insertVertex(Object vertex) {
vertexList.add ( vertex );
}
//插入边
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
numOfEdges++;
}
//删除边
public void deleteEdge(int v1, int v2) {
edges[v1][v2] = 0;
numOfEdges--;
}
4.size(),isEmpty()方法
public int size(){
return seqList.getSize ();
}
public boolean isEmpty() {
Graph <T> node = null;
if (node == null)
return false;
return true;
}
5.广度优先迭代器,深度优先迭代器
public void iteratorBFS(int startIndex){
Deque<Map<String, Object>> nodeDeque = new ArrayDeque<Map<String, Object>>();
Map<String, Object> node = new HashMap<String, Object>();
nodeDeque.add(node);
while (!nodeDeque.isEmpty()) {
node = nodeDeque.peekFirst();
System.out.println(node);
//获得节点的子节点,对于二叉树就是获得节点的左子结点和右子节点
List<Map<String, Object>> children = (List <Map <String, Object>>) node;
if (children != null && !children.isEmpty()) {
for (Map child : children) {
nodeDeque.add(child);
}
}
}
}
public void iteratorDFS(){
Stack<Map<String, Object>> nodeStack = new Stack<Map<String, Object>>();
Map<String, Object> node = new HashMap<String, Object>();
nodeStack.add(node);
while (!nodeStack.isEmpty()) {
node = nodeStack.pop();
System.out.println(node);
//获得节点的子节点,对于二叉树就是获得节点的左子结点和右子节点
List<Map<String, Object>> children = (List <Map <String, Object>>) node;
if (children != null && !children.isEmpty()) {
for (Map child : children) {
nodeStack.push(child);
}
}
}
}
一、实验结果
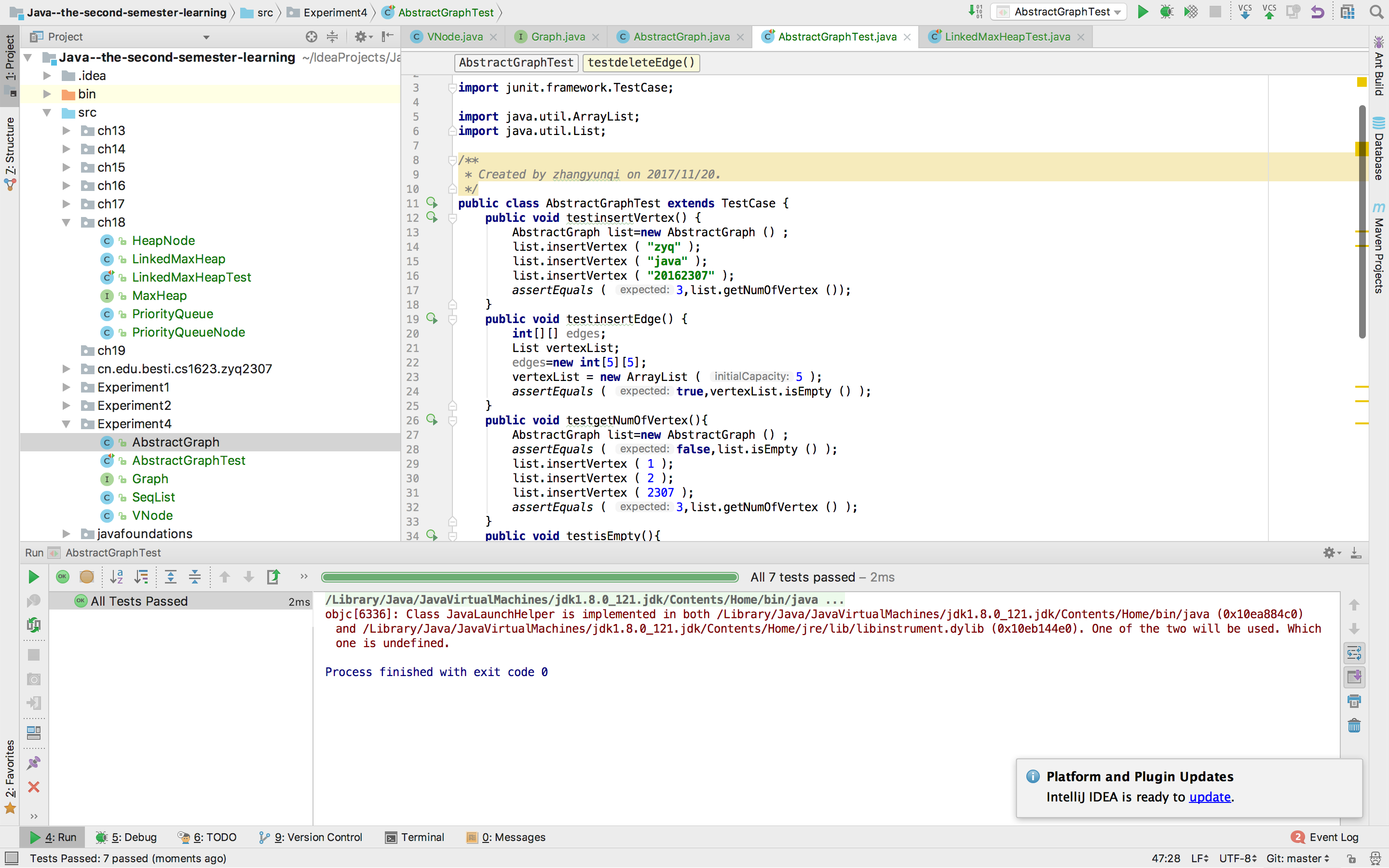
二、实验要求
用十字链表实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
给出伪代码,产品代码,测试代码(不少于5条测试)
二、实验步骤
1.十字链表
把邻接表与逆邻接表结合起来,即有向图的一种存储方法十字链表(Orthogonal List)。
2.对十字链表的理解
入弧表示入边表头指针,指向该顶点的入边表中第一个结点;
出弧表示出边表头指针,指向该顶点的出边表中第一个结点;
弧尾是指弧起点在顶点的下标,
弧头是指弧终点在顶点表中的下标,
同弧头是指入边表指针域,指向终点相同的下一条边
同弧尾是指出边表指针域,指向起点相同的下一条边。
如果是网,还可以再增加一个weight域来存储权值。
- 用十字链表实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法
public static void insertEdge(Edge <Integer> edge, List <Vertex <Integer, Integer>> vertexList) {
int fromVertexIndex = edge.fromVertexIndex;
int toVertexIndex = edge.toVertexIndex;
Vertex <Integer, Integer> fromVertex = vertexList.get ( fromVertexIndex );
Vertex <Integer, Integer> toVertex = vertexList.get ( toVertexIndex );
if (fromVertex.firstOut == null) {
//插入到顶点的出边属性
fromVertex.firstOut = edge;
} else {
// 插入到edge的nextSameFromVertex属性
Edge <Integer> tempEdge = fromVertex.firstOut;
//找到最后一个Edge
while (tempEdge.nextSameFromVertex != null) {
tempEdge = tempEdge.nextSameFromVertex;
}
tempEdge.nextSameFromVertex = edge;
}
if (toVertex.firstIn == null) {
//插入到顶点的入边属性
toVertex.firstIn = edge;
} else {
// 插入到edge的nextSameToVertex属性
Edge <Integer> tempEdge = toVertex.firstIn;
//找到最后一个Edge
while (tempEdge.nextSameToVertex != null) {
tempEdge = tempEdge.nextSameToVertex;
}
tempEdge.nextSameToVertex = edge;
}
}
public void removeVertex(List <Vertex <Integer, Integer>> vertexList){
if (!isEmpty ()){
for (int index=0;index<vertexList.size();index++){
vertexList.remove ( index );
}
}
}
public void removeEdge(Edge<Integer> edge){
if (!isEmpty ()){
edgeCollection.remove ( edge );
}
}
4.size(),isEmpty()
public boolean isEmpty() {
ArrayList <Vertex <Integer, Integer>> vertexList = new ArrayList <> ();
vertexList = null;
if (vertexList == null)
return true;
return false;
}
public int size() {
Edge <Integer> edge = null;
List <Vertex <Integer, Integer>> vertexList = null;
int fromVertexIndex = edge.fromVertexIndex;
int toVertexIndex = edge.toVertexIndex;
Vertex <Integer, Integer> fromVertex = vertexList.get ( fromVertexIndex );
Vertex <Integer, Integer> toVertex = vertexList.get ( toVertexIndex );
if (edge != null && fromVertex != null && toVertex != null)
return vertexList.size ();
return vertexList.size ();
}
5.广度优先迭代器,深度优先迭代器
public Iterator<T> iteratorBFS(int startIndex){ //广度优先遍历
int currentVertex;
LinkedQueue<Integer> traversalQueue = new LinkedQueue <Integer> ();
ArrayIterator<T> iter =new ArrayIterator <T> ();
if (!indexIsValid(startIndex)){
return iter;
}
boolean[] visited =new boolean[numVertices];
for (int vertexIndex=0;vertexIndex<numVertices;vertexIndex++)
visited[vertexIndex]=false;traversalQueue.enqueue ( startIndex );
visited[startIndex]=true;
while (!traversalQueue.isEmpty ()){
currentVertex=traversalQueue.dequeue ();
iter.add (vertices[currentVertex]);
for(int vertexIndex=0;vertexIndex<numVertices;vertexIndex++)
if (adjMatrix[currentVertex][vertexIndex]&&!visited[vertexIndex]){
traversalQueue.enqueue ( vertexIndex );
visited[vertexIndex]=true;
}
}
return iter;
}
public Iterator<T> iteratorDFS(int startIndex){ //广度优先遍历
int currentVertex;
LinkedStack<Integer> traversalStack = new LinkedStack <Integer> ();
ArrayIterator<T> iter =new ArrayIterator <T> ();
boolean[] visited=new boolean[numVertices];
boolean found;
if (!indexIsValid(startIndex)){
return iter;
}
for(int vertexIdx = 0;vertexIdx<numVertices; vertexIdx++){
visited[vertexIdx] =false;
}
traversalStack.push(startIndex);
iter.add(vertices[startIndex]);
visited[startIndex]=true;
while (!traversalStack.isEmpty ()){
currentVertex=traversalStack.peek ();
found=false;
for(int vertexIdx=0; vertexIdx <numVertices&&!found; vertexIdx ++)
if (adjMatrix[currentVertex][vertexIdx]&&!visited[vertexIdx]){
traversalStack.push ( vertexIdx );
iter.add(vertices[vertexIdx]);
visited[vertexIdx]=true;
found=true;
}
if(!found&&! traversalStack.isEmpty())
traversalStack.pop();
}
return iter;
}
二、实验结果
三、实验要求
实现PP19.9
给出伪代码,产品代码,测试代码(不少于5条测试)
三、实验步骤
19.9
创建计算机网络路由系统
输入网路中点到点的线路
以及每条线路使用的费用
系统输出网络中各点之间最便宜的路径
指出不相同的所有位置
public class RoutingSystem {
private class Vertex {
private String vertexLabel; //顶点标识
private List <Edge> adjEdges; //与该顶点邻接的边(点)
private int dist; //顶点间距离
private Vertex preNode;
public Vertex(String vertexLabel) {
this.vertexLabel = vertexLabel;
adjEdges = new LinkedList <> ();
dist = Integer.MAX_VALUE;
preNode = null;
}
}
private class Edge {
private Vertex endVertex;
public Edge(Vertex endVertex) {
this.endVertex = endVertex;
}
}
private Map <String, Vertex> nonDirectedGraph;
private Vertex startVertex;//图的起始顶点
public RoutingSystem(String graphContent) {
nonDirectedGraph = new LinkedHashMap <> ();
buildGraph ( graphContent );
}
private void buildGraph(String graphContent) {
String[] lines = graphContent.split ( "
" );
String startNodeLabel, endNodeLabel;
Vertex startNode, endNode;
for (int i = 0; i < lines.length; i++) {
String[] nodesInfo = lines[i].split ( "," );
startNodeLabel = nodesInfo[1];
endNodeLabel = nodesInfo[2];
endNode = nonDirectedGraph.get ( endNodeLabel );
if (endNode == null) {
endNode = new Vertex ( endNodeLabel );
nonDirectedGraph.put ( endNodeLabel, endNode );
}
startNode = nonDirectedGraph.get ( startNodeLabel );
if (startNode == null) {
startNode = new Vertex ( startNodeLabel );
nonDirectedGraph.put ( startNodeLabel, startNode );
}
Edge e = new Edge ( endNode );
//对于无向图而言,起点和终点都要添加边
endNode.adjEdges.add ( e );
startNode.adjEdges.add ( e );
}
startVertex = nonDirectedGraph.get ( lines[0].split ( "," )[1] );//总是以文件中第一行第二列的那个标识顶点作为源点
}
public void unweightedShortestPath() {
unweightedShortestPath ( startVertex );
}
/*
* 计算源点s到无向图中各个顶点的最短路径
* 需要一个队列来保存图中的顶点,初始时,源点入队列,然后以广度的形式向外扩散求解其他顶点的最短路径
*/
private void unweightedShortestPath(Vertex s) {
//初始化
Queue <Vertex> queue = new LinkedList <> ();
s.dist = 0;
queue.offer ( s );//将源点dist设置为0并入队列
while (!queue.isEmpty ()) {
Vertex v = queue.poll ();
for (Edge e : v.adjEdges) {//扫描v的邻接边(点)
if (e.endVertex.dist == Integer.MAX_VALUE) {//如果这个顶点(e.endVertex)未被访问(每个顶点只会入队列一次)
e.endVertex.dist = v.dist + 1;//更新该顶点到源点的距离
queue.offer ( e.endVertex );
e.endVertex.preNode = v;//设置该顶点的前驱顶点
}//end if
}//end for
}//end while
}
//http://www.cnblogs.com/jmzz/archive/2011/09/26/2190722.html
/* public static int[] Dijsktra(int[][] weight,int start){
//接受一个有向图的权重矩阵,和一个起点编号start(从0编号,顶点存在数组中)
//返回一个int[] 数组,表示从start到它的最短路径长度
String graphFilePath;
graphFilePath = "/Users/zhangyunqi/Desktop/zyq.txt" ;
String graphContent = FileUtil.read(graphFilePath, null);
int n = graphContent.length (); //顶点个数
int[] shortPath = new int[n]; //存放从start到其他各点的最短路径
int[] visited = new int[n]; //标记当前该顶点的最短路径是否已经求出,1表示已求出
//初始化,第一个顶点求出
shortPath[start] = 0;
visited[start] = 1;
for(int count = 1;count <= n - 1;count++) //要加入n-1个顶点
{
int k = -1; //选出一个距离初始顶点start最近的未标记顶点
int dmin = 1000;
for(int i = 0;i < n;i++)
{
if(visited[i] == 0 && weight[start][i] < dmin)
{
dmin = weight[start][i];
k = i;
}
}
//将新选出的顶点标记为已求出最短路径,且到start的最短路径就是dmin
shortPath[k] = dmin;
visited[k] = 1;
//以k为中间点想,修正从start到未访问各点的距离
for(int i = 0;i < n;i++)
{
if(visited[i] == 0 && weight[start][k] + weight[k][i] < weight[start][i])
weight[start][i] = weight[start][k] + weight[k][i];
}
}
return shortPath;
}
*/
//打印图中所有顶点到源点的距离及路径
public void showDistance() {
Collection <Vertex> vertexs = nonDirectedGraph.values ();
for (Vertex vertex : vertexs) {
System.out.print ( vertex.vertexLabel + "<--" );
Vertex tmpPreNode = vertex.preNode;
while (tmpPreNode != null) {
System.out.print ( tmpPreNode.vertexLabel + "<--" );
tmpPreNode = tmpPreNode.preNode;
}
String graphFilePath;
graphFilePath = "/Users/zhangyunqi/Desktop/zyq.txt";
String graphContent = FileUtil.read ( graphFilePath, null );
System.out.println ( "两者之间的距离=" + vertex.dist );
}
}
}
三、实验结果