1672. [SPOJ 375] 难存的情缘
★★★ 输入文件:qtree.in 输出文件:qtree.out 简单对比
时间限制:1 s 内存限制:256 MB
【题目描述】
一天机房的夜晚,无数人在MC里奋斗着。。。
大家都知道矿产对于MC来说是多么的重要,但由于矿越挖越少,勇士们不得不跑到更远的地方挖矿,但这样路途上就会花费相当大的时间,导致挖矿效率低下。
cjj提议修一条铁路,大家一致同意。
大家都被CH分配了一些任务:
zjmfrank2012负责绘制出一个矿道地图,这个地图包括家(当然这也是一个矿,毕竟不把家掏空我们是不会走的),和无数个矿,所以大家应该可以想出这是一个无向无环图,也就是一棵树。
Digital_T和cstdio负责铺铁路。。所以这里没他们什么事,两位可以劳作去了。
这个时候song526210932和RMB突然发现有的矿道会刷怪,并且怪的数量会发生变化。作为采矿主力,他们想知道从一个矿到另一个矿的路上哪一段会最困难。。。(困难值用zjm的死亡次数表示)。
【输入格式】
输入文件的第一行有一个整数N,代表矿的数量。矿的编号是1到N。
接下来N-1行每行有三个整数a,b,c,代表第i号矿和第j号矿之间有一条路,在初始时这条路的困难值为c。
接下来有若干行,每行是“CHANGE i ti”或者“QUERY a b”,前者代表把第i条路(路按所给顺序从1到M编号)的困难值修改为ti,后者代表查询a到b所经过的道路中的最大困难值。
输入数据以一行“DONE”结束。
【输出格式】
对每个“QUERY”操作,输出一行一个正整数,即最大困难值。
【样例输入】
3
1 2 1
2 3 2
QUERY 1 2
CHANGE 1 3
QUERY 1 2
DONE
【样例输出】
1
3
【提示】
对于60%的数据,1<=N<=50
对于100%的数据,1<=N<=10000,1<=c<=1000000,1<=操作次数<=100000
【来源】
由GDFRWMY 改编自SPOJ 375 QTREE
数据by cstdio
啊哈,又来了坑人的树链剖分(太气人了 上一次考试就被它坑惨了) +线段树
多练练也许就好了 所以!(隆重决定 猛敲一遍这一道题 <<意思就是说代码很长且心情愤怒)
这一道题就是用一个树链剖分 放到线段树里
啊 哈 来啦!~~~♪(^∇^*)
大肆纪念 !!调了两天终于做出来了(无比艰辛 心情复杂)
首先这一题有如下几个坑:
1.边权转点权 因为要把这棵树进行树链剖分以后撂到线段树上 那线段树上只能存点的值啊 就要把边权转化为点权 那么这个该怎么办呢
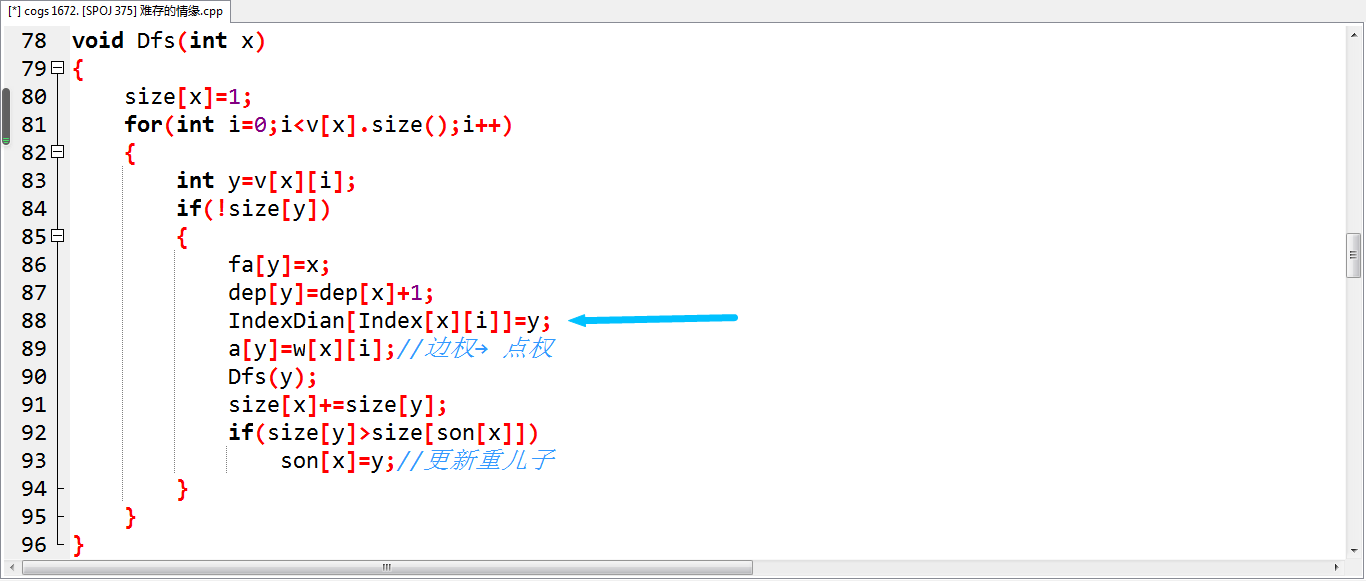
这是我的那个第一个DFS函数 在处理树链剖分的同时 不是会枚举到边嘛 就把边权放在y那个点上(就是放在儿子上),这样子就不用单独再把所有边全部枚举一遍 再把边权放在深度更大的一端上了♪(^∇^*)莫名开心
2.在Change函数中是输入边的编号(按照输入顺序来编号) 把边权改为z
呵呵 这一个方面 其实这个地方我处理的还不是非常好
我后来想到一个方法 就是单独再设一个数组 aindex 数组 和 bindex 数组 aindex[i]表示第i条边的a端点是那一个点 这样子在Change函数的时候直接拿出来用就可以了
我用了一个非常玄学的办法QAQ 再来瞅瞅我的代码
首先我设了两个神奇的数组

那个Index数组 额 就是记录是边(的一个端点)是第几个读入的 IndexDian就是记录第x条边的边权应该放在哪一个点上(是不是非常玄学QAQ 我坚信您现在还没很明白)
再来看看存储:
这是输入各个边的边权的那一段

就是存起来嘛
然后:
再次回到刚才的那个第一个DFS函数

第88行的那个就是说。。。首先那个Index[x][i]里就是说x和v[x][i]之间的那一条边的编号
整个IndexDian[Index[x][i]]=y就是第Index[x][i]条边的边权要放在y(儿子)那个点上QAQ
那么在调用的时候怎么办呢?
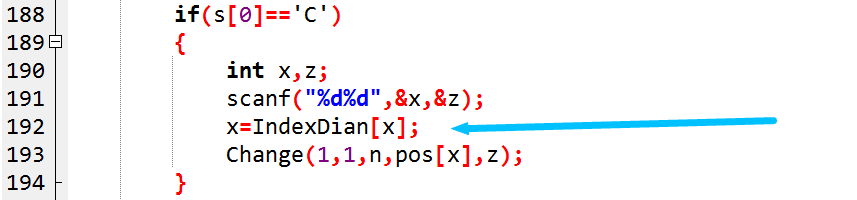
看到那个192行了吗(废话啊)
x不是就是输入边的编号吗 这样子就直接找出来应该修改那一个点的点权即可 ♪(^∇^*)(有点自豪)这样子就变的非常简单啦
3.重头戏:怎样查询从a到b路径上的最大边权
看似简单 然后我就猛敲了一顿 过了样例 就交了上去 结果。。10分!WA了9个点 只A了一个点(我太蒟了)
这到底是为什么呢 ?经过数百次的手造数据的验证 我终于找出了错误的原因
我之前的写法是 直接按照求a到b的路径上的最大点权的做法来做的(看起来没有任何问题啊)
事实上有反例
快看下面这个图 ♪(^∇^*)
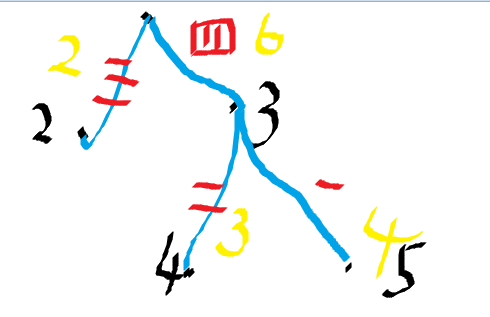
非常粗糙 哈哈不要介意啦 (人家可是很用心地在写博客)
先来解释一下这个图是什么意思吧
黑色的那个12345 自然就是点的编号(最上面的那个1丢了 不要介意嘻嘻(#^.^#))
红色的汉字的 一二三四 就是输入边的顺序(编号)
蓝色的线段(额 这个不需要解释了吧) 就是连上一条边啊
黄色的那个代表边权
按照我们的做法 我们把边权全部放在了点上
那么如果你要是求 2 到 5 路径上最大边权 没问题
你看 2点点权2 1点点权0 3点点权6 5点点权4 那么最大值就是6啦 就是 1-3之间的那条边
(一切看起来都没有任何问题QAQ)
但是如果要是求4-5 路径上最大边权呢?很显然是3-5之间的那个4啊
但是!你的程序如果按照路径最大点权 跑出来的却是6 为什么呢?
原来 你把1-3的边权放在了3上 在4-5的路径上有3 自然3那个点的点权(其实不是4-5路径上的边权)就成了最大值
这可咋整!?(困惑了我一个上午)
我们再来分析一下第一个例子 就是求2-5的最大边权为什么没有出问题 我们惊奇地发现原来因为1点是0
其实这个还是比较好解释和理解的
在把边权撂到深度更大的那个点(简称儿子)以后
a b 两点的 最近公共祖先的值 代表的是最近公共祖先往上(专业术语:深度更小)的那一条边的边权,其实我们是不考虑它的
(仔细想想也许你就明白了)
理解了错误原因后 那么我们怎么处理?这真是一个棘手的问题啊
我们再来观察一下代码
看看那一段LCA

加了一堆+1 的那一段绝望的注释仿佛已经解释了我所经历的一切
就是说那个while函数以后 已经把x和y两个点放到了同一条重链上 为甚么这么说呢?
(答案:自己去看定义!)<<算啦 开玩笑啦~♪(^∇^*)
whike函数的停止条件是top[x]=top[y]那不是就到一条重链上了吗QAQ
然后!奇迹的一段代码来临了
我们把x和y两个点跳到同一条重链上以后 需要把深度更大的那个点(这里定义成了y 你看有个swap函数)往上跳 和x相遇 也就是说要再求一下x和y之间那一段(重链上)的最大值 更新res
然后呢?首先我们知道树链剖分的时候是先走重链 也就是说同一条重链的编号是连续的(自己去看定义!) 所以我们只需要 把x(就是更靠上的那一个点 其实现在就已经是LCA最近公共祖先了)的编号+1传进那个Max函数就可以了(是不是非常机智)
x的编号+1也是非常好理解的 就是x到y之间不是有一条重链吗
>>灵魂画手再次上线

(默默地说:画技太差 我都看不下去了QAQ)
那个紫色的就是一条重链 x和y已经跳到了如图所示的位置
那么3那个点的pos就是1点的pos+1 (不信可以在代码中输出一下pos值瞅一眼♪(^∇^*))
同理4的pos也是3那个点的pos值+1 (话说pos是啥?拍照时的那个吗 NoNoNo 是记录每个点是第几个访问到的)
也就是说如果查询pos[1]+1 到 pos[4] 那么我们就可以非常愉快地把1那个点的点权完美地忽略掉了,就只求出3 4点的点权的较大值 也就是1-3 和 3-4 两条边的边权的较大值
所以这一题就解决了
下面贴出宏伟代码吧♪(^∇^*) 太艰辛了QAQ (<<等于我太蒟了)

1 #include<cstdio> 2 #include<iostream> 3 #include<vector> 4 #define ls (p*2) 5 #define rs (p*2+1) 6 #define mid (l+r>>1) 7 #define INF 0x3f3f3f3f 8 using namespace std; 9 const int maxn=10005; 10 int n,cnt; 11 vector<int> v[maxn],w[maxn],Index[maxn]; 12 int IndexDian[maxn]; 13 int a[maxn];//要把边权转化为点权啊 14 int son[maxn],fa[maxn]; 15 int size[maxn],top[maxn],dep[maxn],dfn[maxn],pos[maxn]; 16 int sum[maxn<<2]; 17 void Dfs(int x) 18 { 19 size[x]=1; 20 for(int i=0;i<v[x].size();i++) 21 { 22 int y=v[x][i]; 23 if(!size[y]) 24 { 25 fa[y]=x; 26 dep[y]=dep[x]+1; 27 IndexDian[Index[x][i]]=y; 28 a[y]=w[x][i];//边权→点权 29 Dfs(y); 30 size[x]+=size[y]; 31 if(size[y]>size[son[x]]) 32 son[x]=y;//更新重儿子 33 } 34 } 35 } 36 void Dfs(int x,int Tp) 37 { 38 top[x]=Tp; 39 dfn[++cnt]=x; 40 pos[x]=cnt; 41 if(son[x]) 42 { 43 Dfs(son[x],Tp);//先走重链 44 } 45 for(int i=0;i<v[x].size();i++) 46 { 47 int to=v[x][i]; 48 if(!top[to]) 49 { 50 Dfs(to,to);//轻链 51 } 52 } 53 } 54 void Build(int p,int l,int r) 55 { 56 if(l==r) 57 { 58 sum[p]=a[dfn[l]]; 59 return; 60 } 61 Build(ls,l,mid); 62 Build(rs,mid+1,r); 63 sum[p]=max(sum[ls],sum[rs]); 64 return; 65 } 66 void Change(int p,int l,int r,int posx,int z) 67 { 68 if(l==r) 69 { 70 sum[p]=z; 71 return; 72 } 73 if(posx<=mid) 74 Change(ls,l,mid,posx,z); 75 else 76 Change(rs,mid+1,r,posx,z); 77 sum[p]=max(sum[ls],sum[rs]); 78 return; 79 } 80 int Max(int p,int l,int r,int s,int t) 81 { 82 if(s>r||t<l) 83 return -INF; 84 if(s<=l&&r<=t) 85 return sum[p]; 86 return max(Max(ls,l,mid,s,t),Max(rs,mid+1,r,s,t)); 87 } 88 int LCA(int x,int y) 89 { 90 int res=-INF; 91 while(top[x]!=top[y]) 92 { 93 if(dep[top[x]]<dep[top[y]]) 94 swap(x,y); 95 res=max(res,Max(1,1,n,pos[top[x]],pos[x])); 96 x=fa[top[x]]; 97 } 98 if(dep[x]>dep[y]) 99 swap(x,y); 100 res=max(res,Max(1,1,n,pos[x]+1,pos[y]));//+1 +1 +1 !!! 101 return res; 102 } 103 int main() 104 { 105 // freopen("qtree.in","r",stdin); 106 // freopen("qtree.out","w",stdout); 107 scanf("%d",&n); 108 for(int i=1;i<n;i++) 109 { 110 int x,y,z; 111 scanf("%d%d%d",&x,&y,&z); 112 v[x].push_back(y); 113 w[x].push_back(z); 114 v[y].push_back(x); 115 w[y].push_back(z); 116 Index[x].push_back(i); 117 Index[y].push_back(i); 118 } 119 Dfs(1); 120 Dfs(1,1); 121 Build(1,1,n); 122 string s; 123 while(cin>>s) 124 { 125 if(s[0]=='D') 126 break; 127 if(s[0]=='C') 128 { 129 int x,z; 130 scanf("%d%d",&x,&z); 131 x=IndexDian[x]; 132 Change(1,1,n,pos[x],z); 133 } 134 if(s[0]=='Q') 135 { 136 int x,y; 137 scanf("%d%d",&x,&y); 138 printf("%d ",LCA(x,y)); 139 } 140 } 141 return 0; 142 }
你以为这篇题解就结束了吗(天哪 至少有2000多字了)
不 你想错了 我们要学会举一反三QAQ
如果题目这样子出
还是告诉你边权,让你求a到b路径上边权的和 QAQ
这应该怎么办呢 其实这个还是比刚才的那个简单多了
只需要求出来和之后减去最近公共祖先LCA的点权即可 因为毕竟是求和 一开始算上LCA也没什么大不了的 但是如果还是简单地按照求路径点权和就不行了 因为最近公共祖先的点权代表的是这条路径外的边的边权 我们要在用朴素(<<呵呵o(* ̄︶ ̄*)o)且简单(<<简单吗╭(╯^╰)╮)的做法 求出来路径大的点权和之后 再减去LCA的点权
所以这一篇全博客园最宏伟的题解到此就结束了QAQ
最后还有一个小彩蛋 至于是什么呢(QAQ♪(^∇^*))点一下下面的那个程序猫的图片就知道啦~
感谢您认真(死撑着)看完了我的题解 啦啦 欢迎关注哦

