查找算法—散列表

散列表

散列表在查找当中使用非常广泛（本文当然也还会说明删除等其他操作）
本文主要说明散列表的两种解决冲突的办法

散列表查找

散列表：对于很多复杂类型的键值，我们可以用一个数组来实现无序的符号表，将键值通过散列函数转化作为数组的索引，查找即对数组进行查找（这里就需要解决冲突）。

散列表的实现分为两步：
1. 散列函数：
将数据的键值转化为数组的一个索引的一个函数。理想情况下，当然是所有的键值，均对应不同的数组索引。但是更多的是，多个不同的键值，通过散列函数之后，有了相同的数组索引，这时候就需要解决这些同意数组索引的不同键值的确定问题。
2. 解决冲突
这是对于上一步骤产生相同的数组索引问题的解决，主要有两种解决冲突的办法。
1>拉链法
2>线性探测法

散列函数

对于不同类型的数据，构造不同的散列函数，当然是最好的。
下面主要是三种常用的散列函数的构造：

1. 平方取中法
   ——先通过求关键字的平方值扩大相近数的差别，然后根据表长度取中间的几位数作为散列函数值。
   ——这种方式中间的几位数都和关键字的每一位都有关，产生的散列地址较为的均匀。
2. 折叠法
   ——将关键字分割成相同的几位数(最后一位可不同)，然后去这几部分的叠加和。
   ——折叠法一般是和除留余法一起使用的。
3. 除留余数法
   ——取关键字被某个不大于散列表表长 m 的数 p 除后所得的余数为散列地址。即 hash(k) = k mod p, p < m。不仅可以对关键字直接取模，也可在折叠法、平方取中法等运算之后 取模。
   ——对 p 的选择很重要，一般取素数或 m ，若 p 选择不好，容易产生碰撞。

对于一些常用的数据类型：如正整数，浮点数，字符串，组合键等。
1>正整数：最常用的就是除留余数法。
2>浮点数：通常是将键值表示为二进制，再使用除留余数法。（Java就是这样处理的）
3>字符串：除留余数法，将字符串的每个字符使用charAt()转化为char值，即是一个非负的16位整数。这种办法确保了字符串的每个字符都能起到作用。
4>组合键：与处理String类似，将每个键值都混合起来，在进行散列函数的处理。

拉链法

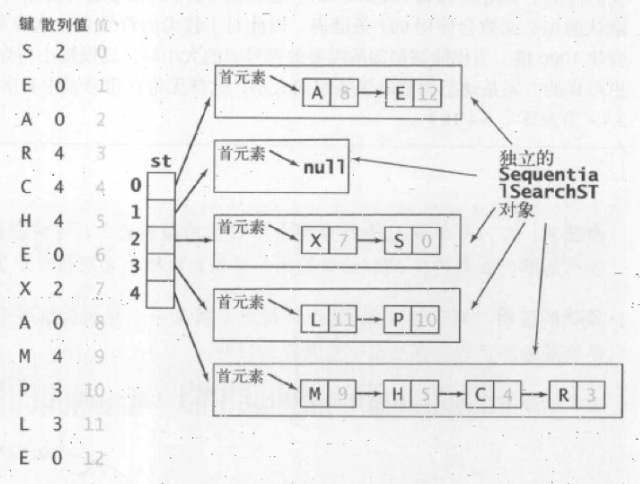
1. 拉链法原理
   将大小为M的数组中的每个索引都指向一个链表，这样对于产生冲突的元素，就都存储在了数组对应索引的链表中。这样查找时，就需要先找到数组对应的索引中，再对索引中的链表进行顺序查找，就能找到目标元素。
   
2. Java实现（只贴关键代码）

        //put(Key,Value)
        // double table size if average length of list >= 10
        if (n >= 10*m) resize(2*m);

        int i = hash(key);

        //judege key is not null
        if (!st[i].contains(key))
            n++;
        st[i].put(key, val);

        //delete(Key)
        int i = hash(key);
        if (st[i].contains(key)) n--;
        st[i].delete(key);

        // halve table size if average length of list <= 2
        if (m > INIT_CAPACITY && n <= 2*m) resize(m/2);

线性探测法

1. 线性探测法原理
   使用大小为M的数组保存N个键值对，用数组中的空位来解决冲突的办法。
   当发生碰撞时（数组的索引已经被前面的键值所占有），我们直接检查散列表的下一个位置（将索引值+K），这样的线性探测，只会有三种结果：
   1>命中，该位置的键与查找键相同；
   2>未命中，键空；
   3>未命中，键值不相同继续查找，索引+K。
   如图：
   

   其中K值不同，也分为不同的线性探测法：
   （ 1 ） d i ＝ 1 ， 2 ， 3 ，——线性探测再散列；
   （ 2 ） d i ＝ 1^2 ，－ 1^2 ， 2^2 ，－ 2^2 ， k^2， -k^2，——二次探测再散列；
   （ 3 ） d i ＝ 伪随机序列 ，——伪随机再散列；

2. Java实现

        //put(Key,Value)
        // double table size if 50% full
        if (n >= m/2) resize(2*m);

        int i;
        for (i = hash(key); keys[i] != null; i = (i + 1) % m) {
            if (keys[i].equals(key)) {
                vals[i] = val;
                return;
            }
        }
        keys[i] = key;
        vals[i] = val;
        n++;

        //delete(Key)
        // find position i of key
        int i = hash(key);
        while (!key.equals(keys[i])) {
            i = (i + 1) % m;
        }

        // delete key and associated value
        keys[i] = null;
        vals[i] = null;

        // rehash all keys in same cluster
        i = (i + 1) % m;
        while (keys[i] != null) {
            // delete keys[i] an vals[i] and reinsert
            Key   keyToRehash = keys[i];
            Value valToRehash = vals[i];
            keys[i] = null;
            vals[i] = null;
            n--;
            put(keyToRehash, valToRehash);
            i = (i + 1) % m;
        }

        n--;

        // halves size of array if it's 12.5% full or less
        if (n > 0 && n <= m/8) resize(m/2);
        assert check();