所谓仿射变换,是一种二维坐标到二维坐标之间的线性变换,保持了变换的图形平直性(直线还是直线,圆弧还是圆弧)和平行性(图形之间相对位置不变)。

仿射变换的实现方法包括平移, 缩放,翻转, 旋转和剪切;

最下面的0 0 1为为了其成为齐次坐标而添加的行元素, 假如是单纯的二维的话只能完成缩放和旋转的操作,故将二维的点改写成三维,这样平移,旋转和缩放都可以写成矩阵的形式;
平移变换:将每一个点移动到(x + tx, y + ty)
则有变换矩阵

缩放变换:将每一点的横坐标放大(缩小)至sx倍, 纵坐标放大(缩小)至sy倍变换矩阵为:

剪切变换:
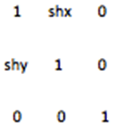
旋转变换:顺时针旋转theta

https://www.cnblogs.com/bnuvincent/p/6691189.html