hihoCoder #1143 : 骨牌覆盖问题·一

#1143 : 骨牌覆盖问题·一

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

骨牌，一种古老的玩具。今天我们要研究的是骨牌的覆盖问题：
我们有一个2xN的长条形棋盘，然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘，一共有多少种不同的覆盖方法呢？
举个例子，对于长度为1到3的棋盘，我们有下面几种覆盖方式：

提示：骨牌覆盖

提示：如何快速计算结果

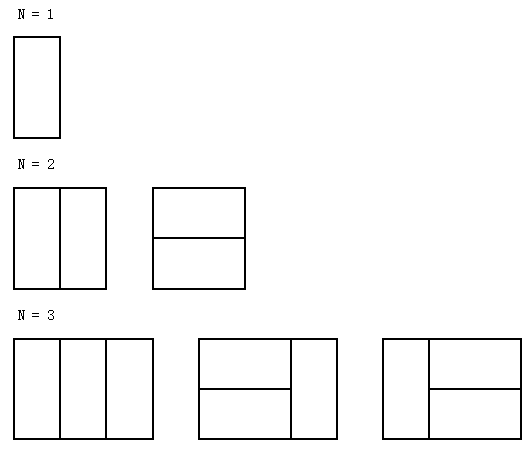
输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 19999997

样例输入

62247088

样例输出

17748018

如果最左边竖着放，那么方法数等于f（n-1）
如果最左边横着放，放么方法数等于f（n-2）
所以f（n）=f（n-1）+f（n-2）
矩阵快速幂

#include<cstdio>
#include<cstring>
#define mod 19999997
using namespace std;
long long a[3][3],ans[3][3],tmp[3][3];
long long n;
void mul(long long s1[3][3],long long s2[3][3])
{
    memset(tmp,0,sizeof(tmp));
    for(int i=1;i<=2;i++)
     for(int j=1;j<=2;j++)
      for(int k=1;k<=2;k++)
       tmp[i][j]=(tmp[i][j]+s1[i][k]*s2[k][j])%mod;
    for(int i=1;i<=2;i++)
     for(int j=1;j<=2;j++)
      s1[i][j]=tmp[i][j];
}
void solve()
{
    for(;n;n>>=1,mul(a,a))
     if(n&1) mul(ans,a);
    printf("%lld
",ans[1][1]);
}
int main()
{
        scanf("%lld",&n);
        if(n==0) 
        {
            printf("0
");
            return 0;
        }
        a[1][1]=1;a[1][2]=1;
        a[2][1]=1;a[2][2]=0;
        ans[1][1]=1; ans[2][1]=1;
        solve();
}