https://acm.hdu.edu.cn/showproblem.php?pid=7018
题意:
n*n*n内放方块,在(x,y,z)位置放的花费是x*y^2*z,如果方块放的位置下面没有方块,方块会因为重力作用下坠。
要求放完之后从上面、左面、前面三个方向看,都是n*n
问最小和最大花费分别是多少
最小花费:
最下面一层全填,然后前面除了最左边一排,左面除了最前面一排
俯视图如下:
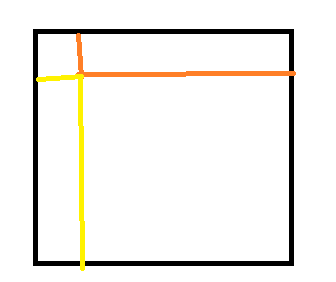
因为画画图可以发现,三面全填一定是满足要求三视图的要求,然后z轴上那一排可以不用填
因为重力作用,不可以去掉x轴或者y轴那一排

三面的花费如下 :
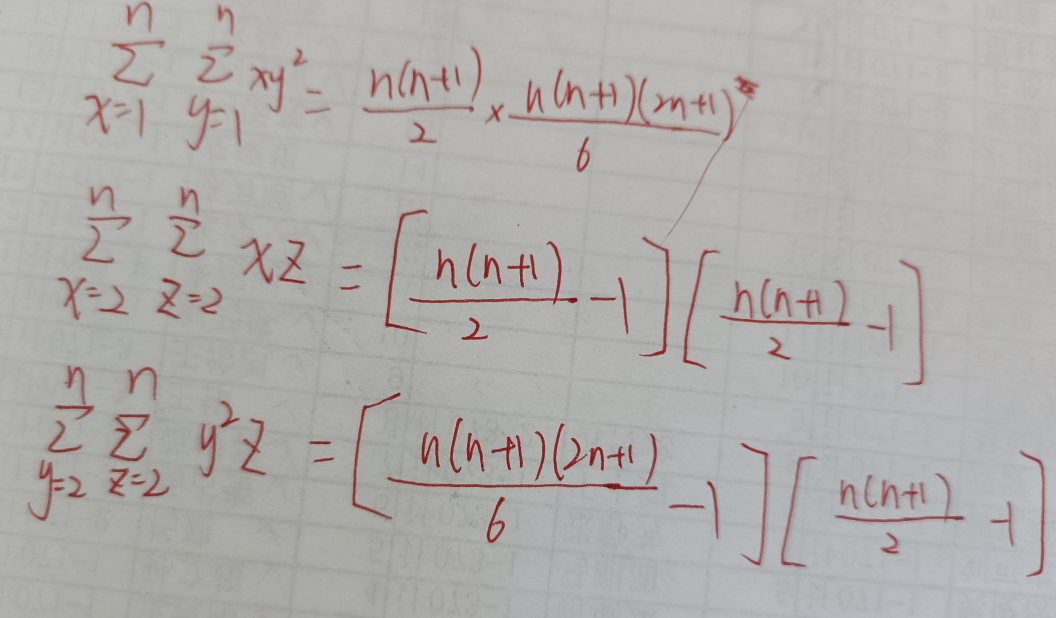
最大花费是n*n*n全填上,但这里有个坑就是应该是每次都放最上面一层,让他下坠
这样z的代价一直是n

#include<bits/stdc++.h> using namespace std; const int mod=1e9+7; int poww(int a,int b) { int c=1; for(;b;a=1ll*a*a%mod,b>>=1) if(b&1) c=1ll*c*a%mod; return c; } int main() { int T,t1,t2,a1,a2; long long n; int inv2=poww(2,mod-2); int inv6=poww(6,mod-2); scanf("%d",&T); while(T--) { scanf("%lld",&n); n%=mod; t1=1ll*n*(n+1)%mod*inv2%mod; t2=1ll*n*(n+1)%mod*(2*n+1)%mod*inv6%mod; a1=(1ll*t1*t2%mod+1ll*(t1-1)*(t1-1)%mod+1ll*(t1-1)*(t2-1)%mod)%mod; a2=1ll*n*n%mod*t2%mod*t1%mod; printf("%d %d ",a1,a2); } }