Codeforces Round #614 (Div. 2) E. Xenon's Attack on the Gangs

http://codeforces.com/contest/1293/problem/E

题意：

给出一棵n个点的树，将0—n-2作为边权，最大化 Σ mex(u,v) 

mex(u,v) 表示u到v的路径上最小的未出现过的自然数

将[0,m]加到一条链上，且这条链上加的边权大小 呈 一个向上凸起的单峰函数状

那么我们可以依次得到[1,m+1]的贡献

原问题转化成 Σ f(x)，f(x)表示 mex(u,v) >=x的(u,v)对数

令sub[u][v]表示以u为根时，v的子树大小

fa[u][v]表示以u为根时，v的父节点

dp[u][v]表示从u到v的一条链的答案

Σ f(x)  x∈[1,m] = f(m)+Σ f(x) x∈[1,m-1] = sub[u][v]*sub[v][u] + max ( dp[u][fa[u][v]] ,dp[v][fa[v][u]]) 

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

#define N 3001

int sub[N][N],fa[N][N];
long long dp[N][N];

int tot,front[N],nxt[N<<1],to[N<<1];

void add(int u,int v)
{
    to[++tot]=v; nxt[tot]=front[u]; front[u]=tot;
    to[++tot]=u; nxt[tot]=front[v]; front[v]=tot;
}

void dfs(int root,int x,int f)
{
    sub[root][x]=1;
    int t;
    for(int i=front[x];i;i=nxt[i])
    {
        t=to[i];
        if(t!=f)
        {
            fa[root][t]=x;
            dfs(root,t,x);
            sub[root][x]+=sub[root][t];
        }
    }
}

long long getans(int u,int v)
{
    if(u==v) return 0; 
    if(dp[u][v]!=-1) return dp[u][v];
    long long k1=getans(u,fa[u][v]),k2=getans(v,fa[v][u]);
    dp[u][v]=sub[u][v]*sub[v][u]+max(k1,k2);
    return dp[u][v];
}

int main()
{
    int n,u,v;
    scanf("%d",&n);
    for(int i=1;i<n;++i)
    {
        scanf("%d%d",&u,&v);
        add(u,v);
    }
    for(int i=1;i<=n;++i) dfs(i,i,0);
    memset(dp,-1,sizeof(dp));
    long long ans=0;
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j)
        {
            dp[i][j]=getans(i,j);
            ans=max(ans,dp[i][j]);
        }
    printf("%lld",ans);
    return 0;
}

E. Xenon's Attack on the Gangs

time limit per test

3 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

INSPION FullBand Master - INSPION

INSPION - IOLITE-SUNSTONE

On another floor of the A.R.C. Markland-N, the young man Simon "Xenon" Jackson, takes a break after finishing his project early (as always). Having a lot of free time, he decides to put on his legendary hacker "X" instinct and fight against the gangs of the cyber world.

His target is a network of nn small gangs. This network contains exactly n−1n−1 direct links, each of them connecting two gangs together. The links are placed in such a way that every pair of gangs is connected through a sequence of direct links.

By mining data, Xenon figured out that the gangs used a form of cross-encryption to avoid being busted: every link was assigned an integer from 00 to n−2n−2 such that all assigned integers are distinct and every integer was assigned to some link. If an intruder tries to access the encrypted data, they will have to surpass SS password layers, with SS being defined by the following formula:

S=∑1≤u<v≤nmex(u,v)S=∑1≤u<v≤nmex(u,v)

Here, mex(u,v)mex(u,v) denotes the smallest non-negative integer that does not appear on any link on the unique simple path from gang uu to gang vv .

Xenon doesn't know the way the integers are assigned, but it's not a problem. He decides to let his AI's instances try all the passwords on his behalf, but before that, he needs to know the maximum possible value of SS , so that the AIs can be deployed efficiently.

Now, Xenon is out to write the AI scripts, and he is expected to finish them in two hours. Can you find the maximum possible SS before he returns?

Input

The first line contains an integer nn (2≤n≤30002≤n≤3000 ), the number of gangs in the network.

Each of the next n−1n−1 lines contains integers uiui and vivi (1≤ui,vi≤n1≤ui,vi≤n ; ui≠viui≠vi ), indicating there's a direct link between gangs uiui and vivi .

It's guaranteed that links are placed in such a way that each pair of gangs will be connected by exactly one simple path.

Output

Print the maximum possible value of SS  — the number of password layers in the gangs' network.

Examples

Input

Copy

3
1 2
2 3

Output

Copy

3

Input

Copy

5
1 2
1 3
1 4
3 5

Output

Copy

10

Note

In the first example, one can achieve the maximum SS with the following assignment:

With this assignment, mex(1,2)=0mex(1,2)=0 , mex(1,3)=2mex(1,3)=2 and mex(2,3)=1mex(2,3)=1 . Therefore, S=0+2+1=3S=0+2+1=3 .

In the second example, one can achieve the maximum SS with the following assignment:

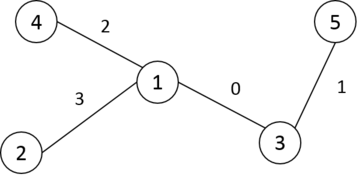
With this assignment, all non-zero mex value are listed below:

• mex(1,3)=1mex(1,3)=1
• mex(1,5)=2mex(1,5)=2
• mex(2,3)=1mex(2,3)=1
• mex(2,5)=2mex(2,5)=2
• mex(3,4)=1mex(3,4)=1
• mex(4,5)=3mex(4,5)=3

Therefore, S=1+2+1+2+1+3=10S=1+2+1+2+1+3=10 .