(题目参考:BF数据结构题单)
普通并查集
代码实现
普通并查集支持 \(2\) 种操作 —— 查询自己在哪个连通块和合并两个联通块(即连边)
操作 1:查询
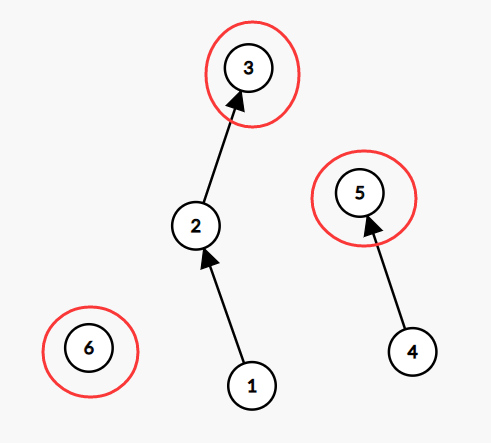
对于我们一个点,查询的连通块记为 \(id_u\),一个连通块的编号为这个连通块中被所有人指向的那个节点。
对于一次查询,我们向上找自己指向的边,然后一步一步这样爬上去。
对于查询,我们可以直接记录下这个节点的 \(id_u\),查找时 \(id_u=\operatorname{find}(id_u)\),这样即路径压缩,可以把复杂度降到 \(O(logn)\)。
如果一个节点的 \(id\) 就是自己,意味着这个点就是被指向的节点。
一开始初始化 \(id_u=u\)
int find(int u){return id[u]==u?u:id[u]=find(id[u]);}
操作 2:合并
若要对 \(2\) 和 \(4\) 进行连边,即合并连通块 \(3\) 和 \(5\),我们直接让 \(5\) 指向 \(3\) (或者 \(3\) 指向 \(5\)) 即可。
void unite(int u,int v){id[find(u)]=find(v);}
题目
连通块类型
[JSOI2008] 星球大战
由于目前了解的并查集还不支持删除操作,而且更加不能在短时间内算出有多少连通块,我们考虑离线操作。
如果两个点合并,那么连通块数就会 \(-1\),所以我们倒叙操作,先合并所有不在询问中的边,然后从最后一个点开始,合并所有和他有边的连通块。
最后存储答案输出即可。
#include<bits/stdc++.h>
using namespace std;
const int N=4e5+9;
struct edge{int u,v;}e[N]; int id[N]; int c[N],tot,ans[N]; bool ap[N];
int find(int i){return i==id[i]?i:id[i]=find(id[i]);}
void unite(int u,int v){id[find(u)]=find(v);}
vector<int>ve[N];
int main(){
int n,m,k; scanf("%d%d",&n,&m); tot=n;
for(int i=1;i<=m;i++) scanf("%d%d",&e[i].u,&e[i].v),e[i].u++,e[i].v++;
for(int i=1;i<=n;i++) id[i]=i;
scanf("%d",&k); for(int i=1;i<=k;i++) scanf("%d",&c[i]),c[i]++,ap[c[i]]=1;
for(int i=1;i<=m;i++){
if((!ap[e[i].u])&&(!ap[e[i].v]))
if(find(e[i].u)!=find(e[i].v)) tot--,unite(e[i].u,e[i].v);
ve[e[i].u].push_back(e[i].v),ve[e[i].v].push_back(e[i].u);
}tot-=k;
for(int i=k;i>=1;i--){
ans[i]=tot; tot++; ap[c[i]]=0;
for(int j=0;j<ve[c[i]].size();j++){
if(find(ve[c[i]][j])!=find(c[i])&&!ap[ve[c[i]][j]]) tot--,unite(ve[c[i]][j],c[i]);
}
}
cout<<tot<<endl;
for(int i=1;i<=k;i++) cout<<ans[i]<<endl;
return 0;
}
贪心加边类型
海滩防御
假设最左边一列为 \(s\),最右边一列为 \(t\),那么对于包括 \(s\) 和 \(t\) 的所有 \(n+2\) 个点进行连边。注意两个防御塔的连边应该是欧几李德距离除以 \(2\)。
然后采用贪心的思想对边用 \(w\) 排序,不停加边直到 \(s\) 和 \(t\) 连通。
#include<bits/stdc++.h>
using namespace std;
const int N=1000009;
struct edge{int u,v;double w;}e[N*2]; int tot;
bool cmp(const edge&a,const edge&b){
return a.w<b.w;
}
struct node{int x,y;}a[N];
double dis(int x0,int y0,int x2,int y2){return sqrt((x0-x2)*(x0-x2)+(y0-y2)*(y0-y2));}
int s,t,id[N];
int find(int i){return id[i]==i?i:id[i]=find(id[i]);}
void unite(int u,int v){id[find(u)]=find(v);}
double ans=0;
int main(){
int n,m;scanf("%d%d",&m,&n);
for(int i=1;i<=n+1;i++) id[i]=i;
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].y,&a[i].x);
for(int i=1;i<n;i++) for(int j=i+1;j<=n;j++)
e[++tot]=(edge){i,j,sqrt((a[i].x-a[j].x)*(a[i].x-a[j].x)+(a[i].y-a[j].y)*(a[i].y-a[j].y))/2};
for(int i=1;i<=n;i++)
e[++tot]=(edge){i,0,a[i].y},e[++tot]=(edge){i,n+1,m-a[i].y};
sort(e+1,e+tot+1,cmp); int ans=0;;
for(int i=1;find(0)!=find(n+1);i++){
if(find(e[i].u)!=find(e[i].v)) id[find(e[i].u)]=find(e[i].v);
ans=i;
}
printf("%.2lf",e[ans].w);
return 0;
}
[HAOI2006] 旅行
考虑到 \(n,m\),数据范围不大,我们先确定一条最小边,然后再贪心加边,知道连通。
最后统计答案即可。
#include<bits/stdc++.h>
using namespace std;
const int M=5e3+9;
struct edge{int u,v,w;}e[M];
bool cmp(const edge&a,const edge&b){
return a.w<b.w;
}
int gcd(int a,int b){
if(b==0) return a;
else return gcd(b,a%b);
}
int n,m,s,t,su[M],id[M],sv[M],ans;
double cans[M],tans=1e9;
void init(){for(int i=1;i<=n;i++)id[i]=i;}
int find(int i){return i==id[i]?i:id[i]=find(id[i]);}
void unite(int u,int v){id[find(u)]=find(v);}
int main(){
scanf("%d%d",&n,&m); init();
for(int i=1;i<=m;i++) scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w),unite(e[i].u,e[i].v);
scanf("%d%d",&s,&t);
if(find(s)!=find(t)) return puts("IMPOSSIBLE"),0;
sort(e+1,e+m+1,cmp);
for(int i=1;i<=m;i++){
init();
for(int j=i;j<=m;j++){
unite(e[j].u,e[j].v);
if(find(s)==find(t)){
sv[i]=e[i].w,su[i]=e[j].w;
cans[i]=e[j].w*1./e[i].w;
break;
}
}
}
for(int i=1;i<=m;i++){
if(!cans[i]) break;
if(cans[i]<tans) tans=cans[i],ans=i;
}
int g=gcd(su[ans],sv[ans]);
if(g==sv[ans]) printf("%d",su[ans]/g);
else printf("%d/%d",su[ans]/g,sv[ans]/g);
return 0;
}
其他类型
[SCOI2010] 连续攻击
这题挺巧妙的。
对于一个攻击,连接两个属性。然后会产生连通块。对于一个连通块,我们从第一个开始,就要选择自己的边。如果有 \(sz-1\) 条边,那么最大的不能被选。否则全都能选。最后处理能选的答案即可。
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+9;
int id[N],mx[N],ed[N],nod[N],x[N],y[N],vst[N];
int find(int i){return i==id[i]?i:id[i]=find(id[i]);}
void unite(int u,int v){id[find(u)]=find(v);}
int main(){
for(int i=1;i<=10000;i++) id[i]=i;
int T; cin>>T; int p=T;
while(T--){
scanf("%d%d",&x[T+1],&y[T+1]); unite(x[T+1],y[T+1]);
}
for(int i=1;i<=p;i++) ed[id[x[i]]]++,vst[x[i]]=vst[y[i]]=1;
for(int i=1;i<=10000;i++) mx[id[i]]=max(mx[id[i]],i),nod[id[i]]++;
for(int i=1;i<=10000;i++) if(ed[id[i]]<nod[id[i]]) vst[mx[id[i]]]=0;
int ans=0; vst[0]=1;
for(;;ans++) if(!vst[ans]) break;
printf("%d\n",ans-1);
return 0;
}
过家家
种类并查集
[NOI2001] 食物链
有三个集合,\(A,B,C\),然后要存储吃/被吃关系的话我们需要拆点。一个点拆成 \(3\) 个点,放入这 \(3\) 个集合,分别是“这个集合的主人”,“吃这个集合里的主人的动物”,“被这个集合里的主人吃的动物”。然后进行存储。如果任意两个自己拆的点在同一连通块那么肯定是 NO,还有很多离谱的情况,判断即可。
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+9;
int id[N];
int find(int i){return id[i]==i?i:id[i]=find(id[i]);}
void unite(int i,int j){id[find(i)]=id[find(j)];}
int n,m,ans;
void init(){for(int i=1;i<=n*3;i++) id[i]=i;}
int main(){
scanf("%d%d",&n,&m); init();
for(int i=1,t,u,v;i<=m;i++){
scanf("%d%d%d",&t,&u,&v); if(u>n||v>n){ans++;continue;}
find(u),find(u+n),find(u+2*n),find(v),find(v+n),find(v+n*2);
if(t==1){
if(id[u+n]==id[v]||id[u+2*n]==id[v]) ans++;
else unite(u,v),unite(u+n,v+n),unite(u+2*n,v+2*n);
}else{
if(find(u)==find(v)) ans++;
else if(id[u+2*n]==id[v]) ans++;
else unite(u+n,v),unite(u+2*n,v+n),unite(u,v+2*n);
}
}
return printf("%d",ans),0;
}
带权并查集
支持操作:并查集的操作,节点到根节点的距离,子树大小等。
代码实现
find 函数路径更新时,要顺便更新自己维护的其他值。
int d[N],s[N]; //到根的距离&块的深度
int find(int u){
if(id[u]==u) return u;
int tmp=id[u]; //!
id[u]=find(id[u]);
d[u]+=d[tmp]; //!
s[u]=s[id[u]];
return id[u];
}
unite 要顺便更新一下带的标记。注意,d 数组更新需要就事论事。具体可以见下面的题目。
void unite(int u,int v){
int idu=find(u),idv=find(v); if(idu==idv) return;
id[idu]=idv;
//d数组更新
s[idv]=(s[idu]+=s[idv]);
}
题目
[NOI2002]银河英雄传说
根节点到总根节点的距离即前面有多少战舰,也就是前面联通块的大小。
#include<bits/stdc++.h>
using namespace std;
const int N=30009;
int id[N],d[N],s[N];
int find(int u){
if(id[u]==u) return u;
int tmp=id[u];
id[u]=find(id[u]);
d[u]+=d[tmp];
s[u]=s[id[u]];
return id[u];
}
void unite(int u,int v){
int idu=find(u),idv=find(v); if(idu==idv) return;
id[idu]=idv;
d[idu]=s[idv];
s[idv]=(s[idu]+=s[idv]);
}
int main(){
int T; cin>>T;
for(int i=1;i<=30000;i++) id[i]=i,s[i]=1;
while(T--){
char c; int u,v; cin>>c>>u>>v;
if(c=='M') unite(u,v);
else printf("%d\n",find(u)!=find(v)?-1:abs(d[u]-d[v])-1);
}
return 0;
}
[USACO04OPEN]Cube Stacking G
这题和上一题差不多,唯一的地方是查询需要改一下。
#include<bits/stdc++.h>
using namespace std;
const int N=100009;
int id[N],d[N],s[N];
int find(int u){
if(id[u]==u) return u;
int tmp=id[u];
id[u]=find(id[u]);
d[u]+=d[tmp];
s[u]=s[id[u]];
return id[u];
}
void unite(int u,int v){
int idu=find(u),idv=find(v); if(idu==idv) return;
id[idu]=idv;
d[idu]=s[idv];
s[idv]=(s[idu]+=s[idv]);
}
int main(){
int T; cin>>T;
for(int i=1;i<=100000;i++) id[i]=i,s[i]=1;
while(T--){
char c; int u,v; cin>>c>>u;
if(c=='M') cin>>v,unite(u,v);
else id[u]=find(u),printf("%d\n",d[u]);
}
return 0;
}