搜索引擎的搜索关键词提示功能不用讲了吧,相信大家都用过.那么他是如何实现的呐?今天就来说一说它底层最基本的原理:Trie 树
什么是“Trie 树”?
Trie 树,也叫“字典树”。顾名思义,它是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。
当然,这样一个问题可以有多种解决方法,比如散列表、红黑树,或者一些字符串匹配(KMP,BM)算法,但是,Trie 树在这个问题的解决上,有它特有的优点。不仅如此,Trie 树能解决的问题也不限于此,我们一会儿慢慢分析。
我们先来看下,Trie 树到底长什么样子。
我举个简单的例子来说明一下。我们有 6 个字符串,它们分别是:how,hi,her,hello,so,see。我们希望在里面多次查找某个字符串是否存在。如果每次查找,都是拿要查找的字符串跟这 6 个字符串依次进行字符串匹配,那效率就比较低,有没有更高效的方法呢?
这个时候,我们就可以先对这 6 个字符串做一下预处理,组织成 Trie 树的结构,之后每次查找,都是在 Trie 树中进行匹配查找。Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。最后构造出来的就是下面这个图中的样子。
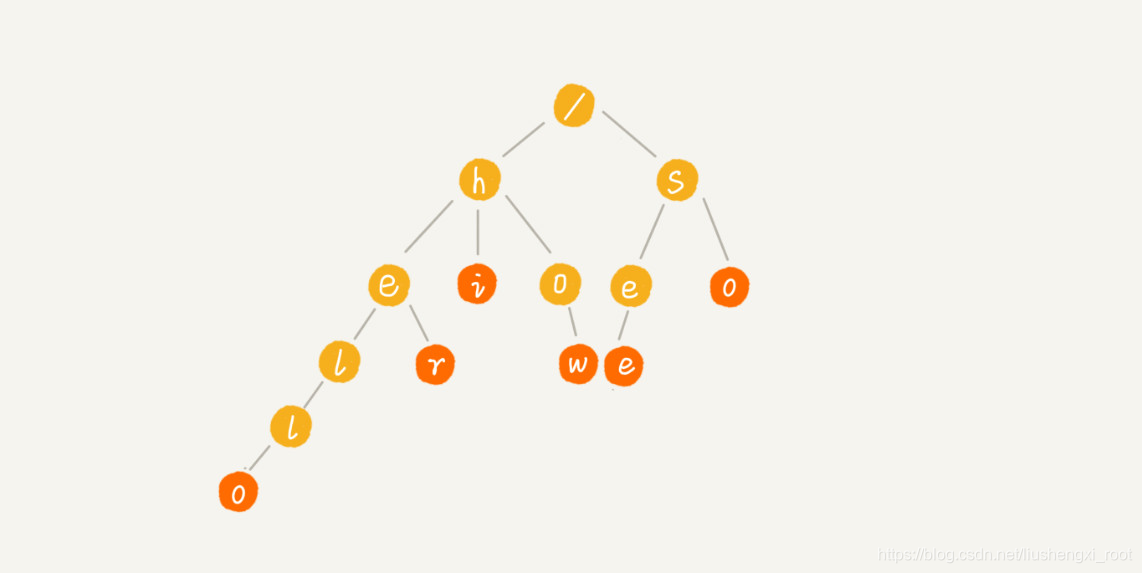
其中,根节点不包含任何信息。每个节点表示一个字符串中的字符,从根节点到红色节点的一条路径表示一个字符串(注意:红色节点并不都是叶子节点)(这里我有点不太懂 )
为了让你更容易理解 Trie 树是怎么构造出来的,我画了一个 Trie 树构造的分解过程。构造过程的每一步,都相当于往 Trie 树中插入一个字符串。当所有字符串都插入完成之后,Trie 树就构造好了。
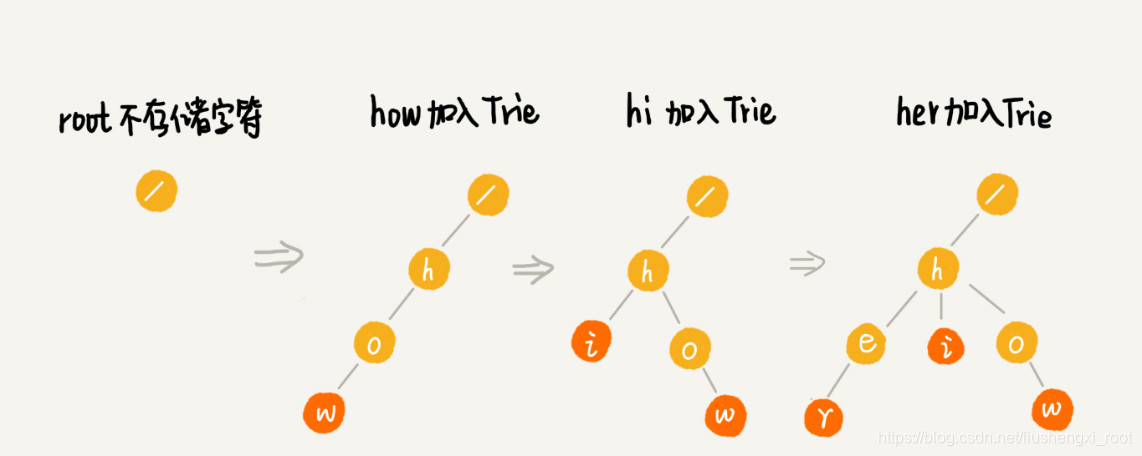
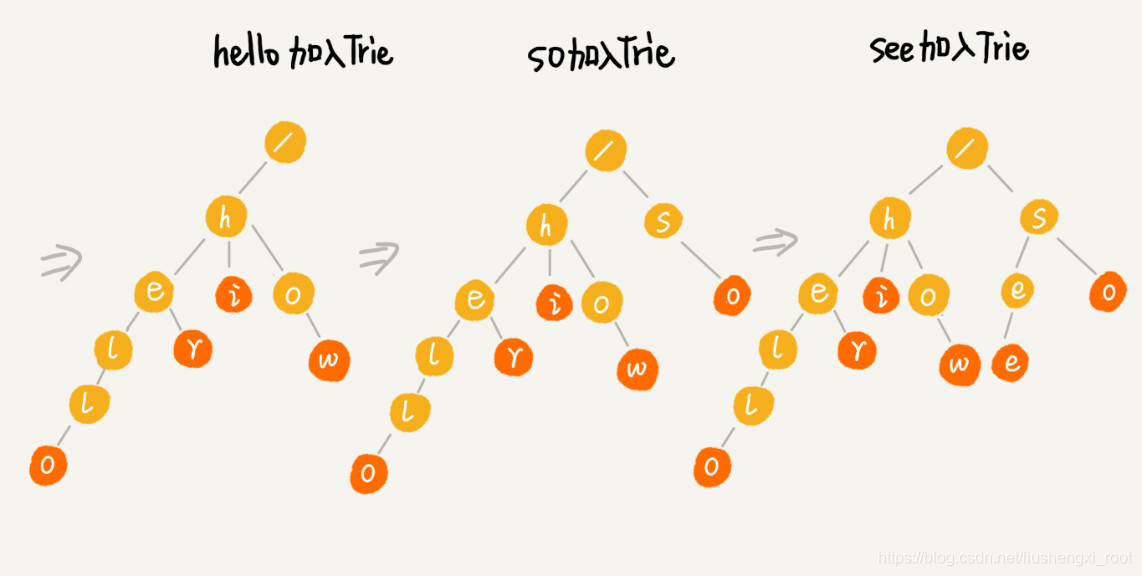
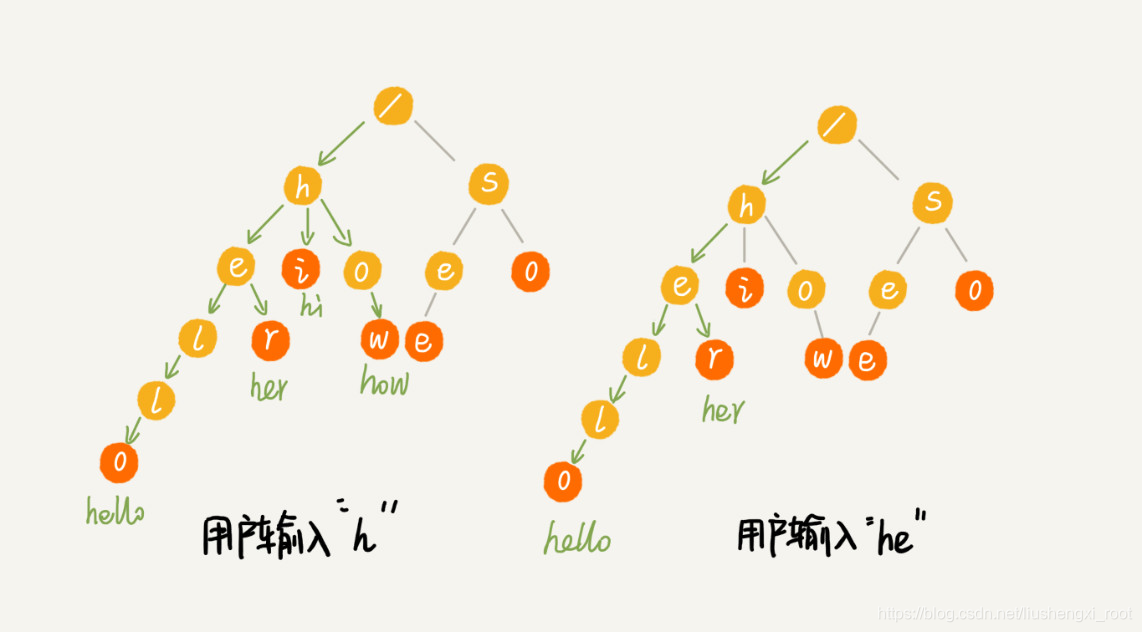
当我们在 Trie 树中查找一个字符串的时候,比如查找字符串“her”,那我们将要查找的字符串分割成单个的字符 h,e,r,然后从 Trie 树的根节点开始匹配。如图所示,绿色的路径就是在 Trie 树中匹配的路径。
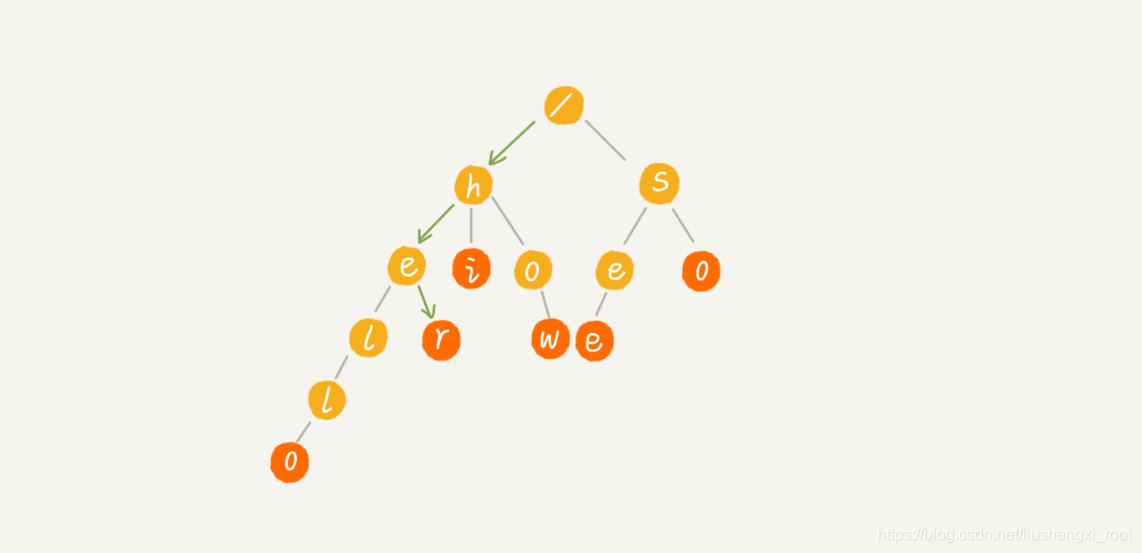
如果我们要查找的是字符串“he”呢?我们还用上面同样的方法,从根节点开始,沿着某条路径来匹配,如图所示,绿色的路径,是字符串“he”匹配的路径。但是,路径的最后一个节点“e”并不是红色的。也就是说,“he”是某个字符串的前缀子串,但并不能完全匹配任何字符串。
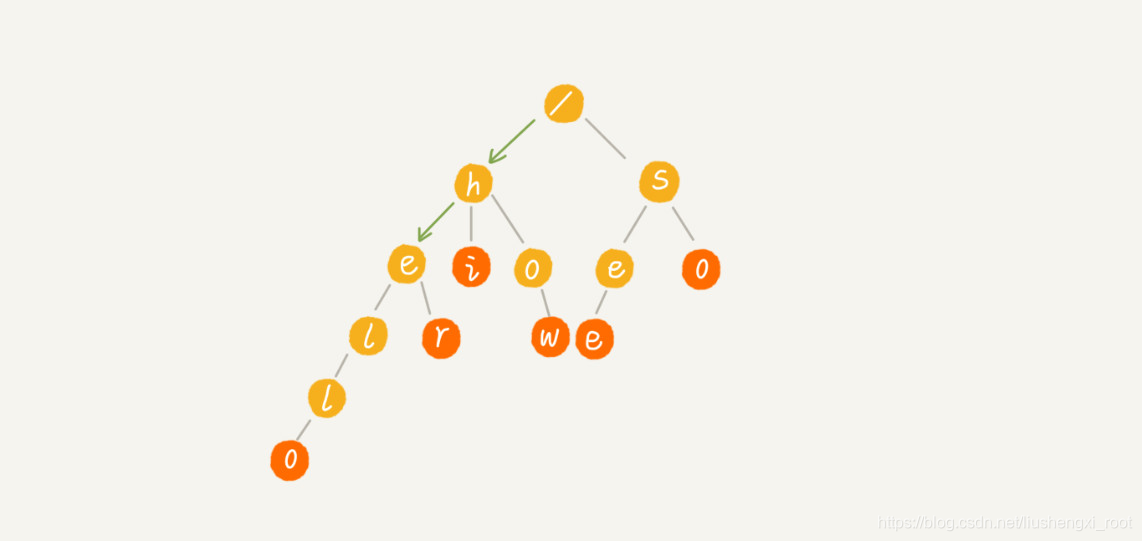
看到这里,我觉得我刚开始想得就是这种树,哈哈哈哈^_^
如何实现一棵 Trie 树?
知道了 Trie 树长什么样子,我们现在来看下,如何用代码来实现一个 Trie 树。
从刚刚 Trie 树的介绍来看,Trie 树主要有两个操作,
- 一个是将字符串集合构造成 Trie 树。这个过程分解开来的话,就是一个将字符串插入到 Trie 树的过程。
- 另一个是在 Trie 树中查询一个字符串。
了解了 Trie 树的两个主要操作之后,我们再来看下,如何存储一个 Trie 树? 从前面的图中,我们可以看出,Trie 树是一个多叉树。我们知道,二叉树中,一个节点的左右子节点是通过两个指针来存储的,那对于多叉树来说,我们怎么存储一个节点的所有子节点的指针呢?
其中一种存储方式,也是经典的存储方式,大部分数据结构和算法书籍中都是这么讲的。还记得我们前面讲到的散列表吗?借助散列表的思想,我们通过一个下标与字符一一映射的数组,来存储子节点的指针。这句话稍微有点抽象,不怎么好懂,我画了一张图你可以看看。
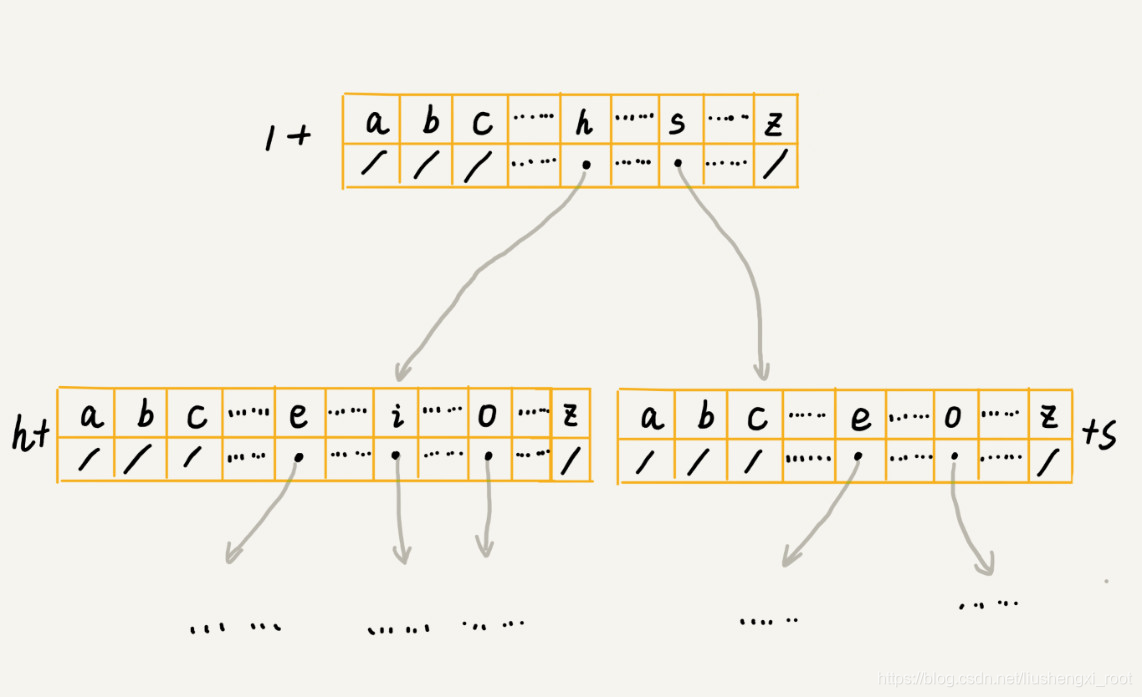
具体实现和结构定义请看代码,我自己觉得这个理解起来还算是比较简单,重点应该放在实现
#include <iostream>
#include <string>
#include <new>
#include <vector>
using namespace std;
class TrieNode
{
public:
explicit TrieNode(char data_t, bool end) : data_(data_t)
{
children_[26] = {nullptr};
isEndingChar_ = end;
}
public:
char data_;
TrieNode *children_[26]; // a-z
bool isEndingChar_;
};
class TrieTree
{
public:
TrieTree()
{
root = new TrieNode('/', false);
}
~TrieTree()
{
destroy(root);
}
void insertString(const string &str)
{
TrieNode *tmp = root;
int num = str.size();
for (int i = 0; i < num; i++)
{
int index = str[i] - 'a';
if (!tmp->children_[index])
{
if (i != num - 1)
tmp->children_[index] = new TrieNode(str[i], false);
else
tmp->children_[index] = new TrieNode(str[i], true);
} // not null
tmp = tmp->children_[index];
}
}
int searchString(string str)
{
TrieNode *tmp = root;
int index = 0;
for (auto i : str)
{
index = i - 'a';
if (!tmp->children_[index])
return -1;
tmp = tmp->children_[index];
}
if (tmp->isEndingChar_)
return 0;
else
return 666;
}
private:
class TrieNode *root;
void destroy(TrieNode *root)
{
if (!root)
return;
for (int i = 0; i < 26; i++)
{
destroy(root->children_[i]);
}
delete root;
root = nullptr;
}
};
int main(void)
{
TrieTree tree;
string insertstrings[5] = {"how", "hi", "hello", "so", "see"};
for (auto t : insertstrings)
{
tree.insertString(t);
}
cout << "Please input the strings :" << endl;
string t1;
while (1)
{
cin >> t1;
switch (tree.searchString(t1))
{
case 0:
cout << "success find " << endl;
break;
case -1:
cout << "not find " << endl;
break;
case 666:
cout << "is public substr " << endl;
break;
}
}
return 0;
}
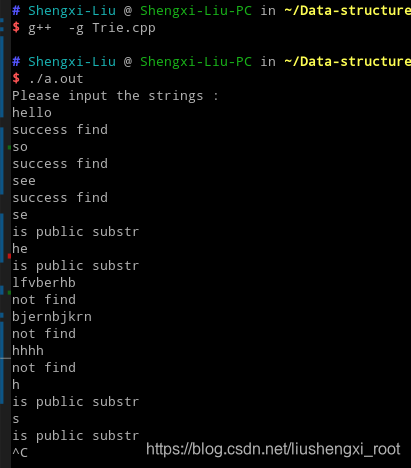
Trie 树的实现,你现在应该搞懂了。现在,我们来看下,在 Trie 树中,查找某个字符串的时间复杂度是多少?
如果要在一组字符串中,频繁地查询某些字符串,用 Trie 树会非常高效。构建 Trie 树的过程,需要扫描所有的字符串,时间复杂度是 O(n)(n 表示所有字符串的长度和)。但是一旦构建成功之后,后续的查询操作会非常高效。
其实这个也比较容易想的来,就像树一样,挨个字符向下找就行了啊,所以说,构建好 Trie 树后,在其中查找字符串的时间复杂度是 O(k),k 表示要查找的字符串的长度。,时间还是主要还是花费在构建树.
Trie 树真的很耗内存吗?
前面我们讲了 Trie 树的实现,也分析了时间复杂度。现在你应该知道,Trie 树是一种非常独特的、高效的字符串匹配方法。但是,关于 Trie 树,你有没有听过这样一种说法:“Trie 树是非常耗内存的,用的是一种空间换时间的思路”。这是什么原因呢?
刚刚我们在讲 Trie 树的实现的时候,讲到用数组来存储一个节点的子节点的指针。如果字符串中包含从 a 到 z 这 26 个字符,那每个节点都要存储一个长度为 26 的数组,并且每个数组存储一个 8 字节指针(或者是 4 字节,这个大小跟 CPU、操作系统、编译器等有关)。而且,即便一个节点只有很少的子节点,远小于 26 个,比如 3、4 个,我们也要维护一个长度为 26 的数组。(其实这个想一下,那就是26262626....)
真正的数据是一个char,但存储的却还有26个指针,得不尝试啊,而且如果符串中不仅包含小写字母,还包含大写字母、数字、甚至是中文,那需要的存储空间就会更多
当然,我们不可否认,Trie 树尽管有可能很浪费内存,但是确实非常高效。那为了解决这个内存问题,我们是否有其他办法呢?
我们可以稍微牺牲一点查询的效率,将每个节点中的数组换成其他数据结构,来存储一个节点的子节点指针。用哪种数据结构呢?我们的选择其实有很多,比如有序数组、跳表、散列表、红黑树等。
假设我们用有序数组,数组中的指针 按照所指向的子节点中的字符的大小顺序排列。查询的时候,我们可以通过二分查找的方法,快速查找到某个字符应该匹配的子节点的指针。但是,在往 Trie 树中插入一个字符串的时候,我们为了维护数组中数据的有序性,就会稍微慢了点。 替换成其他数据结构的思路是类似的,这里我就不一一分析了,你可以结合前面学过的内容,自己分析一下。
实际上,Trie 树的变体有很多,都可以在一定程度上解决内存消耗的问题。比如,缩点优化,就是对只有一个子节点的节点,而且此节点不是一个串的结束节点,可以将此节点与子节点合并。这样可以节省空间,但却增加了编码难度。这里我就不展开详细讲解了,你如果感兴趣,可以自行研究下。
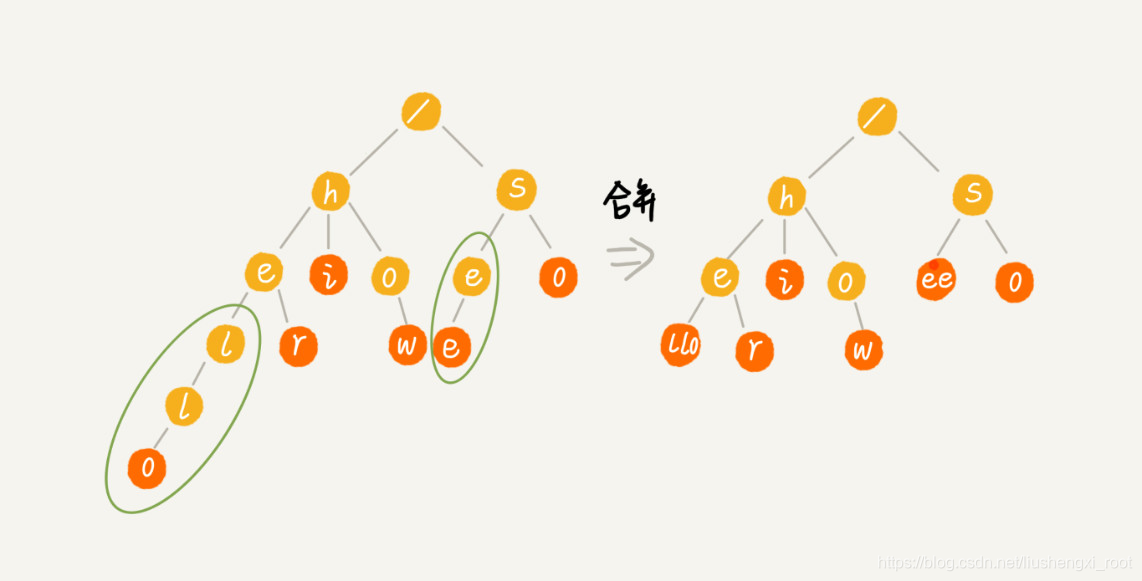
Trie 树与散列表、红黑树的比较
实际上,字符串的匹配问题,笼统上讲,其实就是数据的查找问题。对于支持动态数据高效操作的数据结构,我们前面已经讲过好多了,比如散列表、红黑树、跳表等等。实际上,这些数据结构也可以实现在一组字符串中查找字符串的功能。我们选了两种数据结构,散列表和红黑树,跟 Trie 树比较一下,看看它们各自的优缺点和应用场景。
在刚刚讲的这个场景,在一组字符串中查找字符串,Trie 树实际上表现得并不好。它对要处理的字符串有及其严苛的要求。
-
第一,字符串中包含的字符集不能太大。我们前面讲到,如果字符集太大,那存储空间可能就会浪费很多。即便可以优化,但也要付出牺牲查询、插入效率的代价。
-
第二,要求字符串的前缀重合比较多,不然空间消耗会变大很多。
-
第三,如果要用 Trie 树解决问题,那我们就要自己从零开始实现一个 Trie 树,还要保证没有 bug,这个在工程上是将简单问题复杂化,除非必须,一般不建议这样做。
-
第四,我们知道,通过指针串起来的数据块是不连续的,而 Trie 树中用到了指针,所以,对缓存并不友好,性能上会打个折扣。
综合这几点,针对在一组字符串中查找字符串的问题,我们在工程中,更倾向于用散列表或者红黑树。因为这两种数据结构,我们都不需要自己去实现,直接利用编程语言中提供的现成类库就行了。
讲到这里,你可能要疑惑了,讲了半天,我对 Trie 树一通否定,还让你用红黑树或者散列表,那 Trie 树是不是就没用了呢?是不是今天的内容就白学了呢?
实际上,Trie 树只是不适合精确匹配查找,这种问题更适合用散列表或者红黑树来解决。Trie 树比较适合的是查找前缀匹配的字符串,也就是类似开篇的那种场景。
如何实现搜索引擎的搜索关键词提示功能?
其实这个也不用讲了吧,很简单,显示出来就行了嘛
如果再稍微深入一点,你就会想到,上面的解决办法遇到下面几个问题:
-
我刚讲的思路是针对英文的搜索关键词提示,对于更加复杂的中文来说,词库中的数据又该如何构建成 Trie 树呢?
-
如果词库中有很多关键词,在搜索提示的时候,用户输入关键词,作为前缀在 Trie 树中可以匹配的关键词也有很多,如何选择展示哪些内容呢?
-
像 Google 这样的搜索引擎,用户单词拼写错误的情况下,Google 还是可以使用正确的拼写来做关键词提示,这个又是怎么做到的呢?
你可以先思考一下如何来解决,如果不会也没关系,这些问题,我们会在后面具体来讲解。
实际上,Trie 树的这个应用可以扩展到更加广泛的一个应用上,就是自动输入补全,比如输入法自动补全功能、IDE 代码编辑器自动补全功能、浏览器网址输入的自动补全功能等等。
总的来讲,就是:
- 来做动态集合数据的查找,散列表或者红黑树来。
- 查找前缀匹配的字符串(重复越多越好),比如搜索引擎中的关键词提示功能这个场景,就比较适合用Trie 来解决,也是 Trie 树比较经典的应用场景。
课后题(想到再来答):
我们今天有讲到,Trie 树应用场合对数据要求比较苛刻,比如字符串的字符集不能太大,前缀重合比较多等。如果现在给你一个很大的字符串集合,比如包含 1 万条记录,如何通过编程量化分析这组字符串集合是否比较适合用 Trie 树解决呢?也就是如何统计字符串的字符集大小,以及前缀重合的程度呢?
报一个神奇的bug(真的是玄学):
当我将上面代码的TrieNode改为这样时,他居然他妈的错了:
explicit TrieNode(char data_t, bool end) : data_(data_t), isEndingChar_(end)
{
children_[26] = {nullptr};
}
或者像这样也会错:
explicit TrieNode(char data_t, bool end) : data_(data_t)
{
isEndingChar_ = end;
children_[26] = {nullptr};
}
真的是神奇啊,哈哈哈("马买皮")
参考自:
极客时间 数据结构与算法之美