随笔——算法笔记（未整理）

以下为一些日常收集算法笔记，由于各种原因没有时间整理，暂且记录如下。

程序设计心得：
如果在进行设计某个函数时，没有思路，可以选择

• 引入新的变量
• 引入新的函数
  结合画图板整理思路。

曾经有某位大佬说过：“计算机科学领域的任何问题都可以通过增加一个间接的中间层来解决”，事实上也确实如此。

二分查找

#include <stdio.h>

// 二分查找
int Find(int* arr, int n, int val)
{
	if (NULL == arr || n < 1)return -2;
	int left = 0, right = n - 1;
	int mid = 0;
	int pos = -1;
	while (left <= right)
	{
		//mid = (left + right)/2;
		//mid = (right - left + 1) / 2 + left;
		mid = (right - left + 1) * 0.618 + left;
		if (val < arr[mid])
		{
			right =  mid - 1;
		}
		else  if (val > arr[mid])
		{
			left = mid + 1;
		}
		else
		{
			// 找最左边的数
			while (mid > left&& arr[mid - 1] == val) { --mid; }
			// 找最右边的数
			//while (mid > left&& arr[mid + 1] == val) { ++mid; }
			pos = mid;
			break;
		}
	}
	return pos;
}


// 二分查找，递归版本
int FindVal(int* arr, int left, int right, int val)
{
	int pos = -1;
	int mid = (right - left + 1) / 2 + left;
	if (left < right)
	{
		if (val < arr[mid])
		{
			pos = FindVal(arr, left, mid - 1, val);
		}
		else  if (val > arr[mid])
		{
			pos = FindVal(arr, mid + 1, right, val);
		}
		else
		{
			// 找最左边的数
			while (mid > left&& arr[mid-1] == val) { --mid; }
			// 找最右边的数
			//while (mid > left&& arr[mid + 1] == val) { ++mid; }

			pos = mid;
		}
	}
	return pos;
}

int main()
{
	int arr[] = { 12,12,12,12,13,13,13,13,25,26,47,58,59,69,78,90,100 };
	//int index = FindVal(arr, 0, sizeof(arr) / sizeof(arr[0]), 13);
	int index = Find(arr, sizeof(arr) / sizeof(arr[0]), 13);
	printf("%d", index);
	return 0;
}

递归求斐波拉切数列优化

// 参照此函数的循环优化递归斐波那契数列
int fun(int n)
{
	int a = 1, b = 1, c = 1;
	for(int i=3;i <= n;i++)
	{
		c = a + b;
		b = a;
		a = c;
	}
	return a;
}

// 递归斐波那契数列优化
int fibn(int n, int a, int b)
{
	if (n <= 2)return a;
	else return fibn(n - 1, a + b, a);

}

int fib(int n)
{
	int a = 1, b = 1;
	return fibn(n, a, b);
}

int main()
{
	for (int i = 1; i < 10; i++)
	{

		int n = fun(i);
		int m = fib(i);
		printf("%d %d
", n, m);
	}
	return 0;
}

完全二叉树

void func(int i, int n)
{
	if (i >= n) return;
	else
	{
		func(i + 1, n);
		func(i + 1, n);
	}
}

其中递归的 i 值可以模拟出一个树形，红线表示递归的实际调用顺序。

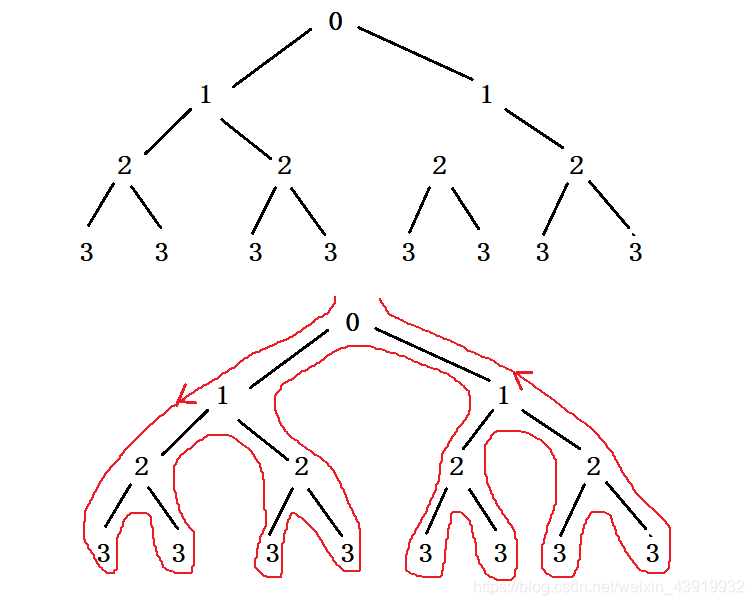
用途：如求一个集合的所有子集 {1,2,3}
在brr[] 中设置三个为分别表示 1，2，3的有和无。比如 brr中 000 表示 arr的1，2，3都不存在，相反 brr 中 111 表示 arr 中 1，2，3都存在，相关代码如下：

void func(int* arr, int* brr, int i, int n)
{
	if (i >= n)
	{
		for (int j = 0; j < n; ++j)
		{
			if (brr[j])
			{
				printf("%d ",arr[j]);
			}
		}
		printf("
");
	}
	else
	{
		brr[i] = 1;
		func(arr, brr, i + 1, n); //左
		brr[i] = 0;
		func(arr, brr, i + 1, n); //右
	}
}

int main()
{
	int arr[] = { 1,2,3 };
	int brr[] = { 1,1,1 };
	func(arr,brr,0,3);
	return 0;
}

输出：

斐波那契数列在计算机科学领域乃至数学上和生活中都有着广泛的用途。比如在程序设计中的兔子产子问题，走台阶问题，青蛙跳荷塘问题，在数学上的杨辉三角也可以中斐波那契数列计算，甚至数学上还给出了直接计算某一项值的公式，在日常生活中如向日葵的葵花籽排列问题等。