题目描述
火车沿途有N 个车站,已知从每一站到每一站的人数,现在查票员只能查K
次票,每次查票可以控制目前在车上的所有乘客的车票,求一个查票方案,使
得查过的不同的乘客尽量多。若有多种最优方案,输出字典序最小的。
注意:对同一个乘客查票多次只会算作一次。
次票,每次查票可以控制目前在车上的所有乘客的车票,求一个查票方案,使
得查过的不同的乘客尽量多。若有多种最优方案,输出字典序最小的。
注意:对同一个乘客查票多次只会算作一次。
输入
第一行正整数N,K. 接下来N − 1 行,第i 行第j 个数描述第i 站上、到第
i + j 站下的乘客个数。
i + j 站下的乘客个数。
输出
单调增的K 个整数,用空格隔开,表示经过哪些站以后查票。
.
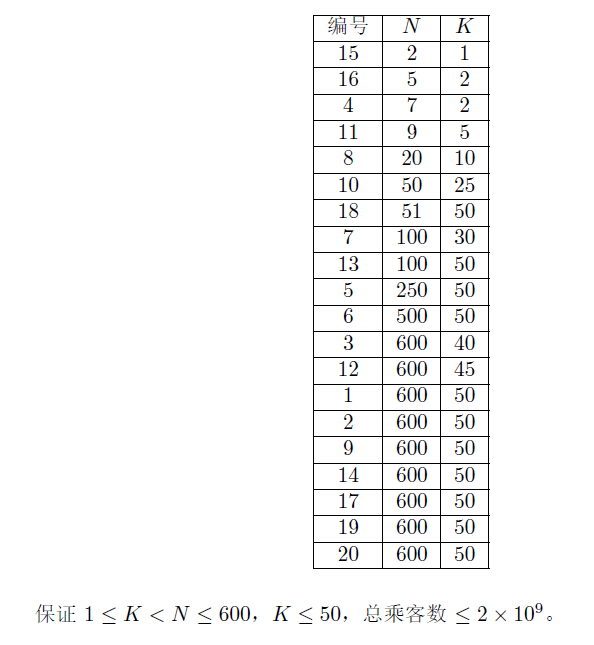
数据范围限制
Solution:
不难看出是道dp题,转移方程也很容易写出来,难点在于两个,一个是如何处理区间总和的问题,一个就是如何输出最优解对应的站数
针对第一个问题,我们可以采用矩阵前缀和的方式,O(N²)预处理之后就可以O(1)得出答案
第二个问题我是抄别人代码的,针对这个问题其实可以类似链表和打擂台的方式去记录每次更新答案之后选择的对应站台,详见Code
Code:
1 #include<bits/stdc++.h>
2 #define max(a,b) a>b?a:b
3 using namespace std;
4 int N,K;
5 int Peo[650][650],Sum[650][650],Pre[650][650],OUTPUT[650],Ans,Num;
6 int f[650][60];
7 int main()
8 {
9 freopen("ticket.in","r",stdin);
10 freopen("ticket.out","w",stdout);
11 scanf("%d%d",&N,&K);
12 for(int i=1;i<N;i++)
13 for(int j=i+1;j<=N;j++)
14 scanf("%d",&Peo[i][j]);
15 for(int i=1;i<=N;i++)
16 for(int j=1;j<=N;j++)
17 Sum[i][j]=Peo[i][j]-Sum[i-1][j-1]+Sum[i-1][j]+Sum[i][j-1];
18 memset(f,128,sizeof(f));
19 f[0][0]=0;
20 for(int i=1;i<=N;i++){
21 for(int j=1;j<=K;j++){
22 for(int k=0;k<i;k++){
23 int temp=Sum[i][N]-Sum[k][N]+Sum[k][i]-Sum[i][i];
24 if (f[i][j]<f[k][j-1]+temp){
25 f[i][j]=f[k][j-1]+temp;
26 Pre[i][j]=k;
27 }
28 if (j==K&&Ans<f[i][j]){
29 Ans=f[i][j];
30 Num=i;
31 }
32 }
33 }
34 }
35 for(int i=Num,j=K;i;i=Pre[i][j--]) OUTPUT[j]=i;
36 for(int i=1;i<=K;i++)
37 cout<<OUTPUT[i]<<" ";
38 return 0;
39 }