数据结构——堆排序（使用Java）

一、简介

　　堆排序（HeapSort）是选择排序的改进版，它可以减少在选择排序中的比较次数，进而减少排序时间，堆排序法用到了二叉树的技巧，它利用堆积树来完成，堆积是一种特殊的二叉树，可分为大根堆和小根堆。

　　大根堆需要具备的条件：

它是一棵完全二叉树

所有节点的值都大于或等于它左右子节点的值

树根是堆积数中最大的

小根堆需要具备的条件： 　

它是一棵完全二叉树

所有节点的值都小于或等于它左右子节点的值

树根是堆积数中最小的

二、核心思想

　　利用大根堆(小根堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

    其基本思想为(大根堆)：

    1)将初始待排序关键字序列(R1,R2....Rn)构建成大根堆，此堆为初始的无须区；

    2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n]; 

    3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

    操作过程如下：

     1)初始化堆：将R[1..n]构造为堆；

     2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。

    因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。

 

三、图例说明

建立初始堆：

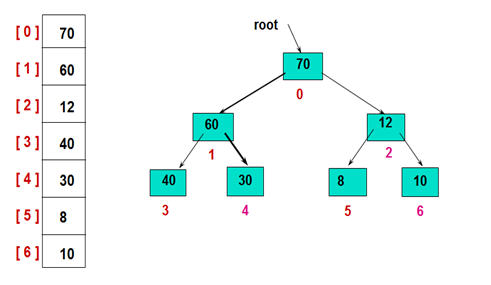
然后，交换堆顶的元素和最后一个元素，此时最后一个位置作为有序区（有序区显示为黄色），然后进行其他无序区的堆调整，重新得到大顶堆后，交换堆顶和倒数第二个元素的位置……

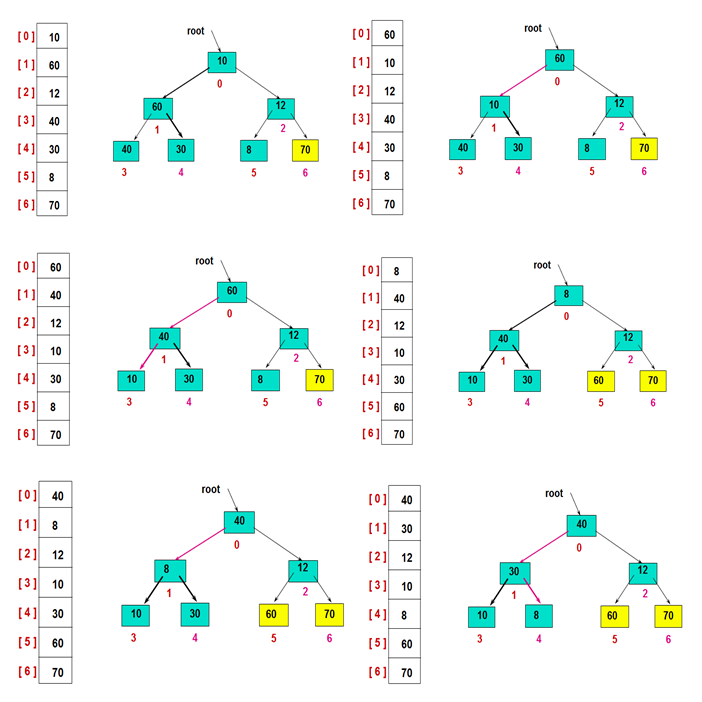
　　重复此过程，直至得到有序序列

　　

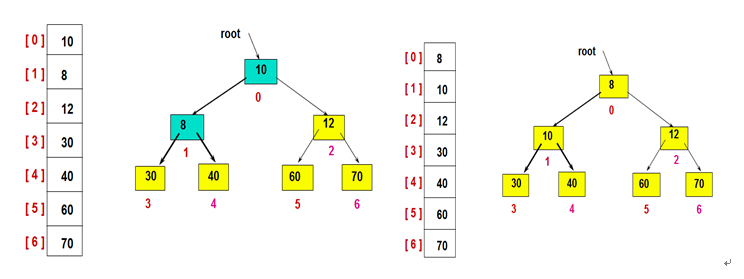
四、代码实现

private static void heapSort(int[] a) {
        int n=a.length;//获取数组长度
        int temp;//用于交换数据
        //构建出初始堆
        for (int i = n/2; i >=0; i--) {
            addDatetoHeap(a,i,n-1);
        }
        System.out.println();
        System.out.print("原始堆：");
        for (int i = 0; i < a.length; i++) {
            System.out.print(a[i]+"  ");
        }
        System.out.println();
        for (int i = n-2; i>=0; i--) {
            //将树根排到有序序列中，然后继续构建堆
            temp=a[i+1];
            a[i+1]=a[0];
            a[0]=temp;
            addDatetoHeap(a, 0, i);
        }
    }

    private static void addDatetoHeap(int[] a, int i, int n) {
        
        int temp=a[i];//记录父节点
        int post=0;//用于判断父节点是否比子节点达
        int j=2*i;//记录子节点
        while(j<=n&&post==0){
            if(j<n){
                if (a[j]<a[j+1]) {//寻找最大节点
                    j++;
                }
            }
                if(temp>=a[j]){//如果树根较大就结束比较过程
                    post=1;
                }else {
                    a[j/2]=a[j];//树根较小，继续比较
                    j=2*j;
                }
            a[j/2]=temp;
        }        
    }
    public static void main(String[] args) {
            int[]a=new int[10];
            Random ran=new Random();
            System.out.println("排序前数组");
            //使用Random方法生成一个随机数组并输出
            for (int i = 0; i < a.length; i++) {
                a[i]=ran.nextInt(100);
                System.out.print(a[i]+"  ");
            }
            //调用排序方法
            heapSort(a);
            //输出排序后方法
            System.out.println("排序后数组");
            for (int i = 0; i < a.length; i++) {
                
                System.out.print(a[i]+"  ");
            }
        }

 五、算法分析

1. 所有情况下时间复杂度均为O（nlogn）。
2. 堆排序是不稳定排序法。
3. 只需一个额外的空间，空间复杂都为O(1).