安全路径——最短路径树+dsu缩边

题目描述

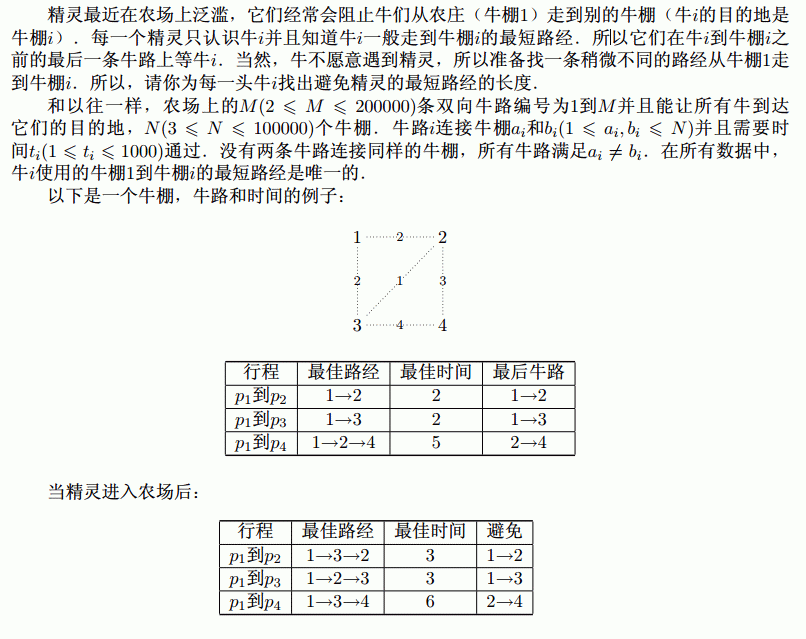
思路

首先想到$dijkstra$跑完之后$build$一棵最短路径树。要找到每个节点i到根的满足要求的最短路，考虑把一些非树边加进去。

对于非树边$(u,v)$，因为节点i上方的边被占领，所以只能选择往下走，从非树边走到别的子树，设$u$属于$i$的子树，$v$不属于，那么$u,v$的$lca$经过$i$，且$i$经过$(u,v)$到根的最短路为$dist[u]+dist[v]-dist[i]+w(u,v)$，这样我们把每条非树边按照$dist[u]+dist[v]+w(u,v)$排序，并查集把$(u,v)$覆盖的边缩起来乱搞一下，从$u,v$不断往上跳即可。

code

#include<iostream>
#include<vector>
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#define pii pair<int,int>
#define mp(x,y) make_pair(x,y)
using namespace std;
const int N=100010;
const int M=200010;
const int inf=1<<30;
struct node
{
    int from,next,to,dis;
}g1[M<<1],g[N<<1];
int h1[N],cnt1;
int head[N],cnt;
int n,m;
int f[N];
 
inline void addedge1(int u,int v,int dis)
{
    g1[++cnt1].next=h1[u];
    g1[cnt1].to=v;
    g1[cnt1].from=u;
    g1[cnt1].dis=dis;
    h1[u]=cnt1;
}
 
inline void addedge(int u,int v,int dis)
{
    g[++cnt].next=head[u];
    g[cnt].to=v;
    g[cnt].dis=dis;
    head[u]=cnt;
}
 
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
 
int dist[N],dep[N];
bool vis[N],on_tree[M<<1];
inline void dijkstra(int s)
{
    priority_queue<pii,vector<pii>,greater<pii> >q;
    for(int i=1;i<=n;i++)vis[i]=0,dist[i]=inf;
    dist[s]=0;q.push(mp(0,s));
    while(!q.empty())
    {
        int u=q.top().second;q.pop();
        if(vis[u])continue;
        vis[u]=1;
        for(int i=h1[u];i;i=g1[i].next)
        {
            int v=g1[i].to;
            if(dist[v]>dist[u]+g1[i].dis)
            {
                dist[v]=dist[u]+g1[i].dis;
                if(!vis[v])q.push(mp(dist[v],v));
            }
        }
    }
}
 
inline void bt(int u)
{
    dep[u]=dep[f[u]]+1;
    for(int i=h1[u];i;i=g1[i].next)
    {
        int v=g1[i].to;
        if(v==f[u])continue;
        if(dist[v]==dist[u]+g1[i].dis)
        f[v]=u,bt(v),addedge(u,v,g1[i].dis),addedge(v,u,g1[i].dis),on_tree[i]=on_tree[i^1]=1;
    }
}
 
struct not_tree
{
    int u,v,w,len;
}e[M];
int tot=0;
int ans[N];
 
bool cmp(not_tree a,not_tree b)
{
    return a.len<b.len;
}
 
struct DSU
{
    int father[N];
    inline void init(int x){for(int i=1;i<=x;i++)father[i]=i;}
    inline int find(int x){return x==father[x]?x:father[x]=find(father[x]);}
    inline void merge(int x,int y){int r1=find(x),r2=find(y);father[r1]=r2;}
}dsu;
 
inline void cover(int x,int y,int len)
{
    x=dsu.find(x);y=dsu.find(y);
    while(x!=y)
    {
        if(dep[x]<dep[y])swap(x,y);
        dsu.merge(x,f[x]);
        ans[x]=len-dist[x];
        x=dsu.find(f[x]);
    }
}
         
int main()
{
    n=read();m=read();
    for(int i=1;i<=m;i++)
    {
        int x=read(),y=read(),z=read();
        addedge1(x,y,z);addedge1(y,x,z);    
    }
    dijkstra(1);
    bt(1);  
    for(int i=1;i<=cnt1;i+=2)
    {
        if(on_tree[i])continue;
        int u=g1[i].from,v=g1[i].to,d=g1[i].dis;
        e[++tot]=(not_tree){u,v,d,dist[u]+dist[v]+d};
    }
    sort(e+1,e+1+tot,cmp);
    dsu.init(n);
    memset(ans,-1,sizeof(ans));
    for(int i=1;i<=tot;i++)
    {
        cover(e[i].u,e[i].v,e[i].len);
    }
    for(int i=2;i<=n;i++)
    {
        if(ans[i]!=-1)printf("%d
",ans[i]);
        else printf("-1
");
    }
     
}