▎前言
一直都想学习这个东西,以为很难,结果发现也不过如此。
只要会些图论的基础就可以了。
▎强连通
☞『定义』
既然叫强连通,那么一定具有很强的连通性。
强连通:就是指在一个有向图中,两个顶点可以互相到达,那么我们就称之为强连通;
强连通图:在一个有向图中,任意两个点都可以互相到达,那么我们称这个图是一个强连通图;
强连通分量:在一个有向图中(不一定是强连通图),一定有很多子图是强连通图,特别的,单独的一个点也是强连通图,而强连通分量则是分成的最大的强连通图。
以下三个红框中的都是强连通分量:
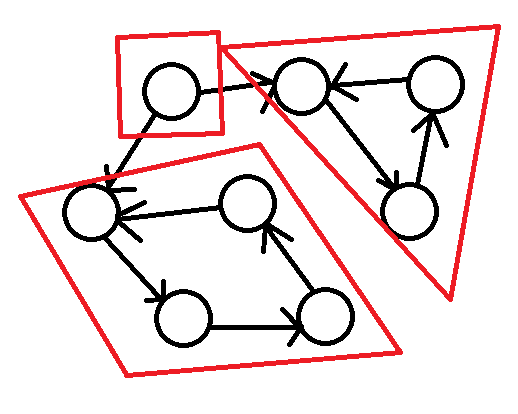
☞『dfs&有向图』
图的遍历如果使用dfs的话,就会形成一棵树的样子。
原理很简单,从任意一个顶点出发,不断扩展,已经遍历过的那么就不再遍历了,直到无法继续遍历(也可能有点会不连接)。
其中这棵树当前节点扩展出的边与这棵树之间有很多关系。
因此在了解了这些之后,我们还得弄清楚一些概念:
假设当前节点为u。
①树枝边:就是u所扩展出的边,且没有访问过;
②前向边:指向DFS树中子树中节点的边;
③后向边:指向DFS树中父亲的边;
④横叉边:指向DFS树中非子树的边。
☞『关系的判定』
首先规定一下:当前节点为u,扩展节点为v,low数组存储的是当前节点及其子树的离根节点最近的节点编号,dfn数组存储的是当前节点被访问的序号。
请看下面的图:
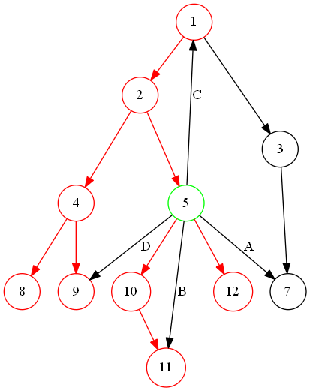
当前节点编号是5,那么:
①树枝边:A边还没有访问过,为树枝边;
②前向边:B边的dfn[v]>dfn[u],说明在子树中,那么这是一条前向边;
③后向边:C边已经访问过了,不在子树中且在栈中,所以这是一条后向边;
④横叉边:D边已经访问过且不在子树中,且已经出栈,所以是一条横叉边。
▎Tarjan算法
☞『什么是Tarjan算法?』
一种由Robert Tarjan提出的求解有向图强连通分量的线性时间的算法。
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。(copy自百度)
☞『算法核心』
对于一条边(u,v),我们在之前的讲解中已经提到了dfn和low数组的意思。
那么初始状态下:low[u]=dfn[u],这应该很好想,初始状态下离根节点最近的节点编号先赋值为自己遍历的编号,和并查集的初始化类似。
每一次扩展时,若边为树枝边,那么我们就使用low[v]来更新low[u],如果是后向边,那么我们就使用dfn[v]来更新。
当low[u] == dfn[u]时,就是一个分割点,要把u之后入栈的元素及u全部弹出栈。
可能有些难理解,推荐一篇别人的博客,图解画得很好,链接在此。
当然,问tarjan算法也会告诉你图解的,小编就不画了。