LSH是我同学的名字,平时我会亲切的称呼他为离骚,老师好,左移(leftshift),小骚骚之类的,最近他又多了一个新的外号:局部敏感哈希(Locally sensitive hashing)。
好了,废话不多说直接转入正题:
『写在前面』局部敏感哈希是一种NOIP禁用的算法(因为使用了随机数),若不感兴趣就无需往下看了。
『什么是LSH?』
LSH就是局部敏感哈希,听着名字就知道和普通的哈希不一样,具体哪里不一样,就先吊吊你的胃口,稍后再说。先来了解LSH的各方面性能:
首先先来思考一个问题:
如果给你一堆数字,然后查找一个数是否在这堆数中存在或者找到一个最相似的数字,你会怎么办?
Answer:
1)首先,我们一定会想到线性查找,直白的来说,这简直就是最慢的一种方法,直接用数组存好后,一个一个来判断,当数据规模小的时候还好,但是,到了规模很大的时候,比如说有1亿个数据时,还能在规定的时间内找到吗?
2)其次,我们会想到二分查找,这种算法运用了分治的思想,将O(n)的时间复杂度降低到了O(log n)的时间复杂度,不过还需要排一次序,但是也费不了多少时间,这种方法相对来说是很可观的,但是有时还满足不了我们的需求。
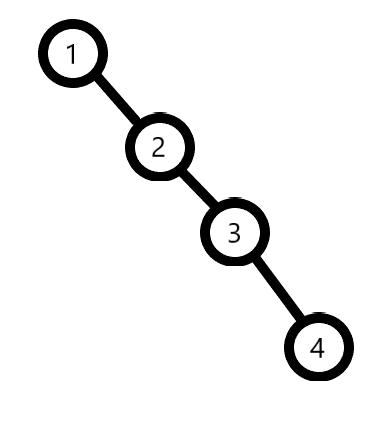
3)这种想法也和 2)差不了多少,但是功能更强大,能够实现维护,插入,删除等一系列操作,没错,它就是二叉查找树,一种用树结构存储的方法,但是有时却很慢,放张图,细细体会吧~
比如说要查找4,那么就一定会全部遍历一遍,显然还是二分查找更快。
4)红黑树&其他平衡树:平衡树的种类很多,这些树能有效避免上图的情况,小编曾写过一篇红黑树博客,想看戳这里,里面也有详细的二叉查找树讲解。
5)好用的当然在后面——哈希算法,这种算法只要操作一遍数后,就可以做到O(1)的速度查找,但是问题却在于如何处理哈希冲突(有关哈希的讲解戳这里),适当的mod正是关键,但是往往我们处理不好这个问题,引起很多问题,比如2000和1000同时对10取模后将都是0,原本差别很大,但是现在没有了差别;再比如1008和1000对10取模后分别是8和0,原本差别不大,但是现在差别相对变大了很多,因此便请出了局部敏感哈希。
局部敏感哈希最大的特点在于保留原来的特性,虽然不一定能完全避免哈希冲突,但是能比一般哈希保留的更好,保持最大可能的相似度。
『哈希思想及实现』小编表示这是一个高冷的话题,离我太遥远,等我学的更好时会自己写的;现在就先放上大牛的博客吧:局部敏感哈希。