【搜索】八皇后

　　这道题应该不陌生吧，这是一道很经典的搜索题。

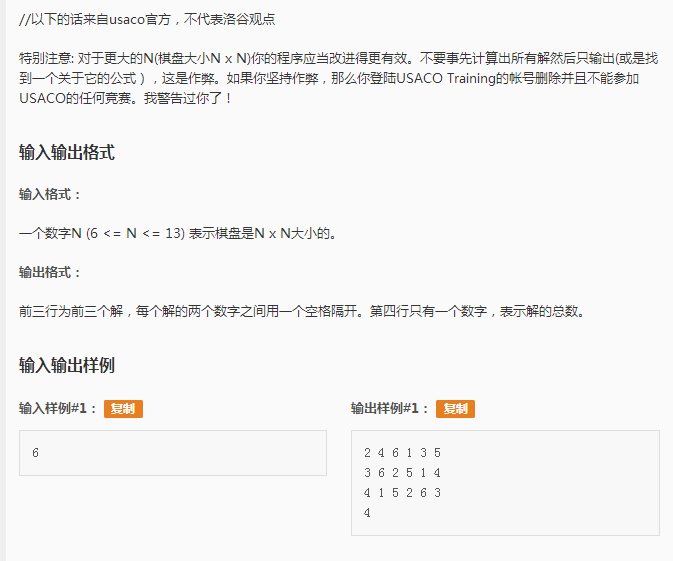
　　总的意思就是说在一个n*n的棋盘上放n个皇后，要求它们互不攻击，求解有多少种情况，并输出前三种。

　　那么开始分析：这毕竟是一道搜索题，搜索最大的弊端是什么，当然是时间复杂度极高，虽然这道题可能不会那么卡，我们完全可以开一个二维数组，然后不停标记不能放的位置。但是你是否想过，一维数组+极少的时间复杂度就可以解决问题。

　　那么具体说一下该怎么放棋子，我们不需要全局的考虑，因为深搜最大的好处是可以简化繁琐的过程，因此我们先考虑只摆一枚棋子，首先假设已经摆好了，那么要进行怎样的操作。

　　

　　如图，比方说现在在第二行第二列的位置上放了一个皇后，那么有哪些点永远不能放棋子呢？

　　

如图，所有红色的格子（包括这个皇后所在的格子）都不能放置皇后了，乍一看，也看不出来什么规律，别着急，把整个图都以二维数组下标的形式标上序号就一目了然了。

　　

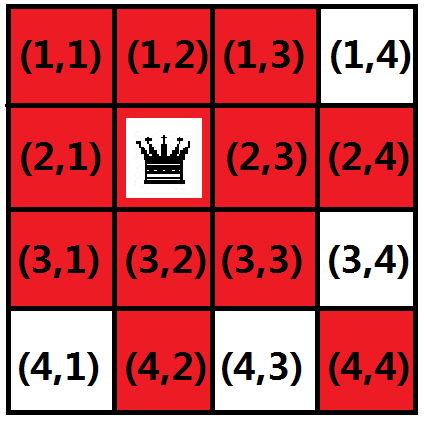
　　按照国际象棋的规则，皇后所能控制的是它所在的行，列，左上到右下的对角线，右上到左下的对角线。那么我们分开看：

　　1）行：如果你够细心，就会发现一行的左边的下标的值都相等，那么我们是不是就可以定义一个一维数组hang（用拼音更好区分），用来存储每行是否被哪一个皇后所霸占，初始赋成0，如果被霸占后，就赋为1，比如说我们要判断（2，4）是否可以放棋子，调用这个数组hang[2]即可知道这一行已经被霸占，所以不能放置。

　　2）列：同上，我们仍然可以定义一个数组用来存储是否被霸占，只需注意所有数是纵坐标相同，和行稍有不同。

　　3）左上到右下的对角线：这当然是一大难点，我们可以通过坐标发现规律，（1，1），（2，2），（3，3），（4，4）都是图上皇后左上到右下所能控制的点，有没有发现这一列的点的横纵坐标差值相同，简单说就是1-1=2-2=3-3=4-4，（不一定非等于零，随着这个皇后位置的改变，差值是会改变的），所以和上文一样，我们定义一个数组duijiaoxian2，如果要判断（i，j）是否能摆放皇后，只需判断duijiaoxian2[i-j]是否等于1即可。

　　4）右上到左下的对角线：同上，只不过是横纵坐标的和相同需要注意就可以了。

　　上文是摆棋时的判断，在摆完每一颗棋后要记得把四个数组相应数值改为1即可。

　　这样，代码就出来了：

#include<iostream>
using namespace std;
int hang[1000],lie[1000],duijiaoxian1[1000],duijiaoxian2[1000],n,lujin[1000],ans,cnt;
void dfs(int x)
{
    if(x>n)
    {
        ans++;
        if(ans<=3)
        {
            for(int i=1;i<=n;i++)
            cout<<lujin[i]<<" ";
            cout<<endl;
        }
        return;
    }
    for(int i=1;i<=n;i++)
    {
        if(lie[i]==0&&duijiaoxian1[i+x]==0&&duijiaoxian2[i-x]==0)
        {
            lie[i]=1;duijiaoxian1[i+x]=1;duijiaoxian2[i-x]=1;
            cnt++;lujin[cnt]=i;
            dfs(x+1);
            cnt--;
            lie[i]=0;duijiaoxian1[i+x]=0;duijiaoxian2[i-x]=0;//要记得回溯
        }
    }
}
int main()
{
    cin>>n;
    dfs(1);
    cout<<ans;
    return 0;
}

　　小编的数组起名都是按拼音起的，便于理解，就不在过多解释了。