树

　　今日小编在睡梦中惊起，发现草稿箱里还有一篇私藏多年的博客，留着也没用，那就发了吧……

       先说说什么是树？

               

　　这是吗？不是；

               

　　这是吗？不是；

                       

　　这是吗？不是；

那么敢问此间树为何物？树就是一堆节点的集合，和图不同的是,树没有回路，如图所示：

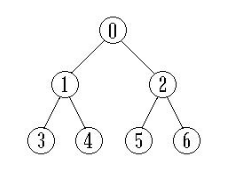
一、树的相关术语

在树最顶端的节点叫做根节点；

每个节点又生出若干个孩子节点；

而这个节点又叫做这些孩子节点的父亲节点；

没有孩子节点的节点叫做叶子节点；

还有什么兄弟节点，祖先节点，孙子节点什么的；

           

如图所示，0节点是根节点，1是0的孩子节点，0是1的父亲节点，3，4，5，6都是叶子节点，blah，blah~

说点更重要的：1）树的度：哪个节点孩子节点最多，那么这个节点孩子节点个数就是这棵树的度；

2）树的层次：从根节点开始算，根节点算第一层，如上图有3层；

3）树的高度：从叶子节点开始，自底向上增加；

4）树的深度：与树的深度相反，自顶向下增加；

二、树的存储与表示

　　树是计算机中所没有的数据结构，是人为提出的概念，所以学树就别想有个什么头文件就能不费吹灰之力就能存储和表示。那你刚学时心中一定会有一个疑问，这么二维的一个东西怎么存？怎么表示？该怎么存就怎么存呗，还得用数组。存的方法就是把二叉树当成满二叉树利用其标号特点储存；表示有父亲表示法，孩子表示法，兄弟表示法等等，小编表示无能为力，手太懒，懒得讲了，毕竟小编也不是很明白，推荐一个最近看到的好博客：https://blog.csdn.net/misayaaaaa/article/details/68941912

三、树的遍历

　　树的遍历不太一样，分为先序遍历（根节点，左子树，右子树），中序遍历（左子树，根节点，右子树），后序遍历（左子树，右子树，根节点），总结一下就是先/中/后遍历根节点的意思呗。小编最开始没学会，自从知道了搜索以后，革命样貌就变得焕然一新了，也没啥可说的，代码在此：

　　

struct s{
    int left;
    int right;
    int value;
}tree[1000];
void firstsearch(int x)
{
    cout<<tree[x].value;
    firstsearch(tree[x].left);
    firstsearch(tree[x].right);
}

　　//这是一个很伪的代码

　　中序后序只要把cout输出部分放到中间和最后即可。

void midsearch(int x)
{
    midsearch(tree[x].left);
    cout<<tree[x].value;
    midsearch(tree[x].right);
}
    

void lastsearch(int x)
{
    lastsearch(tree[x].left);
    lastsearch(tree[x].right);
    cout<<tree[x].value;
}
    

四、往期各种树精选

1.红黑树

2.划分树

3.名字很像树的图：最小生成树

未完待续......