CW一月游记 Day1
好像混了一天..大概听懂了一丢丢...数论之前一直没有时间学 非常尴尬
顺便自己写一下ing ing...
基础讲解
- 如果(a)除以非(0)整数(b)商为整数,且余数为0 -> 我们就说(a)能被(b)整除或者(b)能够整除(a) 记作 (b|a)
- 整除的基本定理 [如果(a|b) (a|c) 那么 (a|bc)] [如果(a|b),那么对于所有整数(c),(a|bc)] [若(a|b),(b|c),则(a|c)]
- 每一个正整数都可以唯一表示为素数(质数)的乘积
- 如果两个数(a)、(b)除以一个(c)的余数相等,说(a)与(b)关于(%c)同余,记作(a≡b(mod c)) -> (a≡b(mod c))成立的充要条件是((a-b)=k*c)
最大公约数和最小公倍数
- 设两个不为(0)的正整数(a)、(b),能使(d|a) && (d|b),那么(d)就是关于a与b的最大公约数,用(gcd(a,b))表示,或者记为((a,b))
- 设两个不为(0)的正整数(a)、(b),能使(a|d) && (b|d),那么(d)就是关于a与b的最小公倍数,用(lcm(a,b))表示,或者记为([a,b])
- 定理:(ab = gcd(a,b) * lcm(a,b))
- 如果(gcd(a,b) = 1) 则(a,b)互质
最大公约数和最小公倍数的定理证明
- 使用唯一分解定理,设
$a = p_{1}{a_{1}}p_{2}{a_{2}}...p_{n}^{a_{n}} ( )b = p_{1}{b_{1}}p_{2}{b_{2}}...p_{n}^{b_{n}} $ - 那么就有
(lcm(a,b)=p_{1}^{max(a_{1},b_{1})}p_{2}^{max(a_{2},b_{2})}...p_{n}^{max(a_{n},b_{n})})
(gcd(a,b)=p_{1}^{min(a_{1},b_{1})}p_{2}^{min(a_{2},b_{2})}...p_{n}^{min(a_{n},b_{n})})
最大公约数的求解
- 名称:欧几里得算法(辗转相除法)
- 利用公式 (gcd(a,b) = gcd(b,a mod b)),时间复杂度((logb))
- 证明:
设(r = a%b,r = a-kb)
设(d)是(a,b)的公约数,则(d|a,d|b),则(d|r)
则(d)是(b,a%b)的公约数
设(d)是(b,a%b)的公约数,同理可证(d)是(a,b)的公约数
则(gcd(a,b)=gcd(b,a%b)) - 代码:(递归版)
int gcd(int x,int y)
{
return b?gcd(y,x%y):x
}
质数筛法((2n)写法 直接上代码)
void int_prime(int x)
{
for (int i=2;i<=x;i++)
{
if(!flag[i]) pre[too++] = i;
for (int j=0;j<tot && pre[j]<=m/i;j++)
{
flag[i*pre[j]] = 1;
if(i % pre[j] == 0) break;
}
}
}
质数筛法例题
CodeForces 114E Double Happiness
hdu 1999 不可摸数
拓展欧几里得
- 婓蜀定理:对于不完全为(0)的非负整数(a,b),(gcd(a,b))表示(a,b)的最大公约数,必然存在整数对(x,y),使得(gcd(a,b)=ax+bx)
- 欧几里得算法静止的状态是:(a=gcd,b=0)即当(x=1,y=0)时,这就是最终状态
拓展欧几里得证明
- 设(x,y)和(x1,y1)时两组解,且满足:
由(a*x+b*y = gcd(a,b))
(b*x_{1}+(aModb)*y_{1} = gcd(b,aModb))
得(a*x+b*y=b*x_{1}+(a%b)*y_{1})
设(k=a/b,r=a%b),则(r=a-k*b),代入上式得
(a*x+b*y=b*x_{1}+(a-a/b*b)*y_{1})
(a*x+b*y=a*y_{1}+b*(x_{1}-a/b*y_{1}))
得(x=y_{1})
(y_{1}=x_{1}-a/b*y_{1})
通解(x = x_{0}+(b/gcd)*t)
(y=y_{0}-(a/gcd)*t)
拓展欧几里得代码(放上代码和应用)
int exgcd(int a,int b,int &x,int &y)
{
if(b == 0) { x = 1;y = 0;return a; }
int temp = exgce(b,a%b,x,y);
int t = x;x = y;y = t-a/b*y;
return temp;
}
- 应用:
- 求解不定方程(ax+by=c)
- 求解线性同余方程
- 求解模的逆元
解不定式方程(ax+by=c)
将方程两遍同时除以(gcd(a,b)),设(a' = a/gcd(a,b),b'=b/gcd(a,b),c'=c/gcd(a,b)),则方程变形为a'x+b'y = c',因为a',b'互相质,所以(gcd(a',b') = 1)
由拓展欧几里得定理知一定的存在(x_{0},y_{0})使得(a'x_{0},b'y_{0}=1)则可由(exgcd)求出(x_{0},y_{0}),将上式两边同时乘以(gcd(a,b))得:
(a'gcd(a,b)x_{0}+b'gcd(a,b)y_{0}=gcd(a,b) ==> ax_{0} + by_{0} = gcd(a,b) ==> ax_{0} + by_{0} = c/c'),
所以方程的解(x_{1} = x_{0} * c' = c/d*x_{0},y_{1} = y_{0} * c' = c/d * y_{0})为方程的一组解,则方程(ax+bx=c)的通解是
(x = x_{1} + b/d*k = c/d*x_{0} + b/d*k)
(y = y_{1} - a/d*k = c/d*y_{0} - a/d*k)
解模线性方程
- 对于线性同余方程:(ax≡m(Mod b))转化为(ax+by=m)则可以直接求解
- (a≡b(Mod c))成立的充要条件是((a-b)=k*c)
- ((ax-m) = by)
- 如:(5x≡2(Mod 3))转换为(5x+3y=2)
- (d=1,x_{0}=-1,y_{0}=2)
- 通解:(x=-2+3t,y=4-5t)
乘法逆元
- 存在(x)使得(ax ≡ 1(mod p)) 则称(x)是(a)关于(p)的乘法逆元
- 定理:(a)关于(p)的乘法逆元存在的充要条件是(gcd(a,p) = 1)
- 逆元有什么作用呢?
当要求((a/b)modp)时,且(a)很大,我们就求(b)关于(p)的惩罚逆元(x),则有((a/b)modp = (a*x)modp) - 证明:
根据(b*x≡1(mod p))有(b*x=p*y+1)
则(x=(p*y+1)/b)
把(x)代入((a*x)modp)得:
((a*(p*y+1)/b)mod p)
(=((a*p*y)/b+a/b) mod p)
(=[((a*p*y)/b)modp+(a/b)] modp)
(=[(p*(a*y)/b) modp +(a/b)]mod p)
(p*[(a*y)/b]mod p=0)
求解逆元
- (5x≡1(mod3))逆元为(2)
- (ax≡1(modp))等价于(ax+py=1)
- 当(gcd(a,p)!=1)的时候是没有解的,这也是(a*x+b*y=c)有解的充要条件:(c%gcd(a,b)==0)
- 解有无数,如何求解最小正整数解?
- 用(x_{0}%p)就是最小解,为什么?
- 由通解知(x = x_{0}+(p/gcd)*t) 其中(gcd=1) 所以(x=x_{0}+p*t) 由于最小解为((0,p))之间,所以(x=x_{0}%p)
- 如果(x_{0})为负数,让(x_{0})对(abs(p)),然后结果再加上(abs(p))就行了
逆元例题
观察归纳法 - 费马小定理
- 假设(p)是质数,且(gcd(a,p)=1),那么(a^{p-1}≡1(mod p))即:假如(a)是整数,(p)是质数,且(a、b)互质,那么(a)的((p-1))次方除以(p)的余数恒等于(1)
- 应用:
如果对于任意满足(1≤b<p)的(b)下式都成立
(b^{p-1}≡1(modp))
则(p)必定是一个质数
其实我们不必验证那么多,据说验证一次错误的概率为(1/4),所以一般验证(10)个质数就可以了
快速幂
- 求解a^n%k
直接上代码(二分)((logn))
int mul(int x,int y,int k)
{
int ans = 1;x = x % k;
while(x)
{
if(x&1) ans = (ans * x) % k;
x = (x * x) % k;
x >>= 1;
} return ans;
}
- 如果该算法乘法溢出 我们会用到慢速乘法(乘法改成加法的形式)
long long mul(long long x,long long y,long long k)
{
long long ans = 0;
for (long long i=y;i;i>>=1)
{
if(i & 1) ans = (ans + x) % k;
x = (x + x) % k;
} return ans % k;
}
long long mull(long long x,long long y,long long k)
{
long long ans = 1;
for (long long i=y;i;i>>=1)
{
if(i & 1) ans = mul(ans,x) % k;
x = mul(x,x) % k;
} return ans % k;
}
欧拉函数
-
对于正整数(n),欧拉函数是指少于或等于(n)的数中与(n)互质的数的数学
-
例如(φ(8)=4),因为(1,3,5,7)均和(8)互质
-
通式:
(φ(x)=x(1-1/p_{1})(1-1/p_{2})(1-1/p_{3})(1-1/p_{4})...(1-1/p_{n})),其中(p_{1},p_{2}...p_{n})为(x)的所有质因数,(x)是不为(0)的整数 (φ(1)=1)(唯一和(1)互质的数((≤1))就是(1)本身(注意:每种质因子只有一个)比如(12 = 2*2*3)那么(φ(12) = 12 * (1-1/2) * (1-1/3) = 4)
若(n)是质数(p)的(k)次幂,(φ(n)=p^{k}-p^{k-1}=(p-1)p^{k-1}),因为除了(p)的倍数外,其他数都跟(n)互质
设(n)为正整数,以(φ(n))表示不超过(n)且与(n)互素的正整数的个数,成为(n)的欧拉函数值,这里函数(φ:N->N,n->φ(n))成为欧拉函数 -
与(n)互质的所有数的和(sum=n*[φ(n)/2])
-
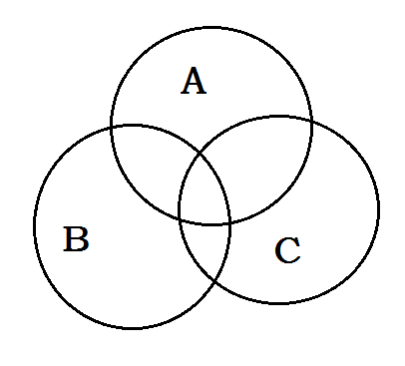
证明:容斥原理
-
(A∪B∪C =A+B+C - A∩B - B∩C - C∩A + A∩B∩C)
-
那么容斥的算法是:(|U|) - 不满足(A_{1})的元素个数-不满足(A_{2})的元素个数....+不满足(A_{1})和(A_{2})的元素个数+....-不满足(A_{1}、A_{2})和(A_{2})的元素个数-....
-
(<1001)与(1001)互质的数一共有多少个?
-
分析:由于(1001 = 7*11*13),所以就是找不到被(7,11,13)整除的数
-
解答:(1~1001)中,有(7)的倍数(1001/7=143(个)) 有(11)的倍数(1001/11 = 91)(个),有(13)(个),有(7*13=91)的倍数(1001/91 = 11)(个),有(11*13=143)的倍数(1001/143 = 7)(个),有(1001)的倍数(1)个
-
由容斥原理知:在(1~1001)中,能被(7)或(11)或(13)整除的数有((143+91+77) - (13+11+7) + 1 = 281)(个),从而不能被(7、11)或(13)整除的数有(1001-281=720)(个),也就是说,小于(1001)与(1001)互质的数有(720)个
-
(p_{1},p_{2},p_{3}....p_{k})为(n)的质因子
-
与(n)不互质的数的个数为:
(n/p_{1}+n/p_{2}+...+n/p_{k}-n/(p_{1}*p_{2})-...-n/(pk-1*p_{k})-n/(p1*p2*p3)-...-n/(p_{k}-2*p_{k}-1*p_{k})-...+n/(p_{1}*p_{2}*...*p_{k})) -
所以与(n)互质的数的个数为:
$φ(n)