贝叶斯判定准则:最小化总体风险,只需在每个样本上选择能使条件风险R(c|x)最小的类别标记
一、极大似然估计
1.估计类的常用策略:先假定其具有某种确定的概率分布形式,再基于训练样本对概率分布的参数进行估计。即概率模型的训练过程就是参数估计过程。
2.参数估计两大学派:频率主义学派和贝叶斯学派。
(1)频率主义:参数虽然未知,但却是客观存在的固定值,因此,可通过优化似然函数等准则来确定参数值(最大似然)。
(2)贝叶斯学派:参数是未观察到的随机变量,本身也可以有分布,因此,可假定参数服从一个先验分布,然后基于观察到的数据来计算参数的后验分布。
二、朴素贝叶斯
(1)思想:对于给定的待分类项x,通过学习到的模型计算后验概率分布,即:在此项出现的条件下各个目标类别出现的概率,将后验概率最大的类作为x所属的类别。后验概率根据贝叶斯定理计算。
(2)关键:为避免贝叶斯定理求解时面临的组合爆炸、样本稀疏问题,引入了条件独立性假设。 即假设各个特征之间相互独立
(3)工作原理:
贝叶斯公式:
![]()

对条件概率做了条件独立假设,公式为:

(4)工作流程:
1)准备阶段:确定特征属性,并对每个特征属性进行适当划分,然后由人工对一部分待分类项进行分类,形成训练样本。
2)训练阶段:对每个类别计算在样本中的出现频率p(y),并且计算每个特征属性划分对每个类别的条件概率p(yi | x);
3)应用阶段:使用分类器进行分类,输入是分类器和待分类样本,输出是样本属于的分类类别。 采用了属性条件独立性假设,d:属性数目,xi为x在第i个属性上的取值。
四、示例
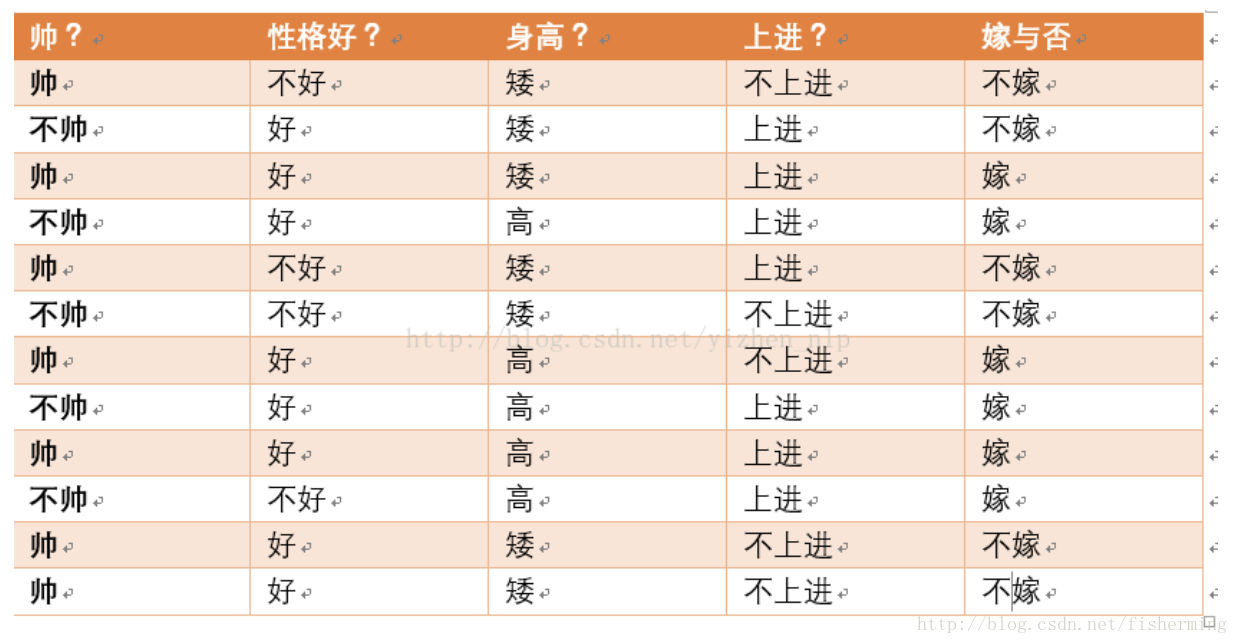
现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
这是典型的二分类问题,按照朴素贝叶斯的求解,转换为P(嫁|不帅、性格不好、矮、不上进)和P(不嫁|不帅、性格不好、矮、不上进)的概率,最终选择嫁与不嫁的答案。
这里我们根据贝特斯公式:
由此,我们将(嫁|不帅、性格不好、矮、不上进)转换成三个可求的P(嫁)、P(不帅、性格不好、矮、不上进|嫁)、P(不帅、性格不好、矮、不上进)。进一步分解可以得:
P(不帅、性格不好、矮、不上进)=P(嫁)P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)+P(不嫁)P(不帅|不嫁)P(性格不好|不嫁)P(矮|不嫁)P(不上进|不嫁)。
P(不帅、性格不好、矮、不上进|嫁)=P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)
将上面的公式整理一下可得:
P(嫁)=1/2、P(不帅|嫁)=1/2、P(性格不好|嫁)=1/6、P(矮|嫁)=1/6、P(不上进|嫁)=1/6。
P(不嫁)=1/2、P(不帅|不嫁)=1/3、P(性格不好|不嫁)=1/2、P(矮|不嫁)=1、P(不上进|不嫁)=2/3
但是由贝叶斯公式可得:对于目标求解为不同的类别,贝叶斯公式的分母总是相同的。所以,只求解分子即可
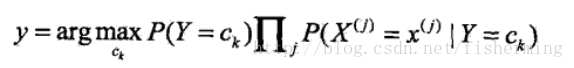
于是,对于类别“嫁”的贝叶斯分子为:P(嫁)P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)=1/2 * 1/2 * 1/6 * 1/6 * 1/6=1/864
对于类别“不嫁”的贝叶斯分子为:P(不嫁)P(不帅|不嫁)P(性格不好|不嫁)P(矮|不嫁)P(不上进|不嫁)=1/2 * 1/3 * 1/2 * 1* 2/3=1/18。
经代入贝叶斯公式可得:P(嫁|不帅、性格不好、矮、不上进)=(1/864) / (1/864+1/18)=1/49=2.04%
P(不嫁|不帅、性格不好、矮、不上进)=(1/18) / (1/864+1/18)=48/49=97.96%
则P(不嫁|不帅、性格不好、矮、不上进) > P(嫁|不帅、性格不好、矮、不上进),则该女子选择不嫁!
五、面试内容
1、贝叶斯分类器与贝叶斯学习不同:
前者:通过最大后验概率进行单点估计;
后者:进行分布估计。
2、后验概率最大化准则意义?
<==>期望风险最小化(只需要对每一项逐个最小化)
3、朴素贝叶斯需要注意的地方?
(1)给出的特征向量长度可能不同,这是需要归一化为通长度的向量(这里以文本分类为例),比如说是句子单词的话,则长度为整个词汇量的长度,对应位置是该单词出现的次数。 (2)计算要点:
4、经典提问:Navie Bayes和Logistic回归区别是什么?前者是生成式模型,后者是判别式模型,二者的区别就是生成式模型与判别式模型的区别。
1)首先,Navie Bayes通过已知样本求得先验概率P(Y), 及条件概率P(X|Y), 对于给定的实例,计算联合概率,进而求出后验概率。也就是说,它尝试去找到底这个数据是怎么生成的(产生的),然后再进行分类。哪个类别最有可能产生这个信号,就属于那个类别。
优点:样本容量增加时,收敛更快;隐变量存在时也可适用。
缺点:时间长;需要样本多;浪费计算资源 2)相比之下,Logistic回归不关心样本中类别的比例及类别下出现特征的概率,它直接给出预测模型的式子。设每个特征都有一个权重,训练样本数据更新权重w,得出最终表达式。梯度法。
优点:直接预测往往准确率更高;简化问题;可以反应数据的分布情况,类别的差异特征;适用于较多类别的识别。
缺点:收敛慢;不适用于有隐变量的情况。
六、朴素贝叶斯的优缺点
优点:
(1) 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
(2)分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
缺点:
朴素贝叶斯假设属性之间相互独立,这种假设在实际过程中往往是不成立的。在属性之间相关性越大,分类误差也就越大。
七、项目使用
sklearn中有3种不同类型的朴素贝叶斯:
高斯分布型:用于classification问题,假定属性/特征服从正态分布的。
多项式型:用于离散值模型里。比如文本分类问题里面我们提到过,我们不光看词语是否在文本中出现,也得看出现次数。如果总词数为n,出现词数为m的话,有点像掷骰子n次出现m次这个词的场景。
伯努利型:最后得到的特征只有0(没出现)和1(出现过)。
八、相关理论基础
1、词集模型:对于给定文档,只统计某个侮辱性词汇(准确说是词条)是否在本文档出
2、词袋模型:对于给定文档,统计某个侮辱性词汇在本文当中出现的频率,除此之外,往往还需要剔除重要性极低的高频词和停用词。因此,词袋模型更精炼,也更有效。
3.数据预处理——向量化
向量化、矩阵化操作是机器学习的追求。从数学表达式上看,向量化、矩阵化表示更加简洁;在实际操作中,矩阵化(向量是特殊的矩阵)更高效。仍然以侮辱性文档识别为例:
首先,我们需要一张词典,该词典囊括了训练文档集中的所有必要词汇(无用高频词和停用词除外),还需要把每个文档剔除高频词和停用词;
其次,根据词典向量化每个处理后的文档。具体的,每个文档都定义为词典大小,分别遍历某类(侮辱性和非侮辱性)文档中的每个词汇并统计出现次数;最后,得到一个个跟词典一样大小的向量,这些向量有一个个整数组成,每个整数代表了词典上一个对应位置的词在当下文档中的出现频率。
最后,统计每一类处理过的文档中词汇总个数,某一个文档的词频向量除以相应类别的词汇总个数,即得到相应的条件概率,如P(x,y|C0)。有了P(x,y|C0)和P(C0),P(C0|x,y)就得到了,用完全一样的方法可以获得
P(C1|x,y)。比较它们的大小,即可知道某人是不是大坏蛋,某篇文档是不是侮辱性文档了。
九、算法总结
不同于其它分类器,朴素贝叶斯是一种基于概率理论的分类算法;
特征之间的条件独立性假设,显然这种假设显得“粗鲁”而不符合实际,这也是名称中“朴素”的由来。然而事实证明,朴素贝叶斯在有些领域很有用,比如垃圾邮件过滤;
在具体的算法实施中,要考虑很多实际问题。比如因为“下溢”问题,需要对概率乘积取对数;再比如词集模型和词袋模型,还有停用词和无意义的高频词的剔除,以及大量的数据预处理问题,等等;
总体上来说,朴素贝叶斯原理和实现都比较简单,学习和预测的效率都很高,是一种经典而常用的分类算法。