题目:
给定长度为N的数列A,以及M条指令,每条指令可能是以下两种之一:
1、“1 x y”,查询区间 [x,y] 中的最大连续子段和,即 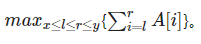
2、“2 x y”,把 A[x] 改成 y。
对于每个查询指令,输出一个整数表示答案。
输入格式
第一行两个整数N,M。
第二行N个整数A[i]。
接下来M行每行3个整数k,x,y,k=1表示查询(此时如果x>y,请交换x,y),k=2表示修改。
输出格式
对于每个查询指令输出一个整数表示答案。
每个答案占一行。
数据范围
N≤500000,M≤100000
输入样例:
5 3
1 2 -3 4 5
1 2 3
2 2 -1
1 3 2
输出样例:
2
-1
解题报告:
区间最大连续子段和,根据区间的可见性,咱们要在线段树的基础上增加lmax,rmax,分别是管理前缀最带子段和和后缀最大子段和,
然后再区间[l,r]这个区间的最大子段和就是左区间的最大子段和,右区间的最大子段和,以及左右区间结合在一起中间的最大子段和。
ac代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 5 const int maxn=500001; 6 ll maxx(ll a,ll b,ll c) 7 { 8 return max(a,max(b,c)); 9 } 10 struct node 11 { 12 int l,r; 13 ll lmax,rmax,sum,dat; 14 //lmax 区间最大前缀和 15 //rmax 区间最大后缀和 16 //dat 最大子段和 17 //sum 区间全加起来的值 18 int mid() 19 { 20 return (l+r)>>1; 21 } 22 }tree[maxn<<2]; 23 24 void pushup(int rt) 25 { 26 tree[rt].lmax=maxx(tree[rt<<1].sum,tree[rt<<1].sum+tree[rt<<1|1].lmax,tree[rt<<1].lmax); 27 tree[rt].rmax=maxx(tree[rt<<1|1].sum,tree[rt<<1|1].sum+tree[rt<<1].rmax,tree[rt<<1|1].rmax); 28 tree[rt].dat=maxx(tree[rt<<1].dat,tree[rt<<1|1].dat,tree[rt<<1].rmax+tree[rt<<1|1].lmax); 29 tree[rt].sum=tree[rt<<1].sum+tree[rt<<1|1].sum; 30 } 31 32 void build(int l,int r,int rt) 33 { 34 tree[rt].l=l; 35 tree[rt].r=r; 36 if(l==r) 37 { 38 scanf("%lld",&tree[rt].dat); 39 tree[rt].sum=tree[rt].lmax=tree[rt].rmax=tree[rt].dat; 40 return; 41 } 42 int m=tree[rt].mid(); 43 build(l,m,rt<<1); 44 build(m+1,r,rt<<1|1); 45 pushup(rt); 46 } 47 void update(int rt,int x,int y) 48 { 49 if(tree[rt].l==tree[rt].r) 50 { 51 tree[rt].sum=tree[rt].lmax=tree[rt].rmax=tree[rt].dat=y; 52 return; 53 } 54 int m=tree[rt].mid(); 55 if(x<=m) 56 update(rt<<1,x,y); 57 else 58 update(rt<<1|1,x,y); 59 pushup(rt); 60 } 61 62 node query(int rt,int l,int r) 63 { 64 if(tree[rt].l==l&&tree[rt].r==r) 65 { 66 return tree[rt]; 67 } 68 int m=tree[rt].mid(); 69 if(m>=r) 70 { 71 return query(rt<<1,l,r); 72 } 73 else if(m<l) 74 { 75 return query(rt<<1|1,l,r); 76 } 77 else 78 { 79 node ls=query(rt<<1,l,m); 80 node rs=query(rt<<1|1,m+1,r); 81 node ans; 82 ans.dat=maxx(ls.dat,rs.dat,ls.rmax+rs.lmax); 83 ans.lmax=maxx(ls.sum,ls.lmax,ls.sum+rs.lmax); 84 ans.rmax=maxx(rs.sum,rs.rmax,rs.sum+ls.rmax); 85 ans.sum=ls.sum+rs.sum; 86 return ans; 87 } 88 } 89 int main() 90 { 91 int n,m; 92 cin>>n>>m; 93 build(1,n,1); 94 int i,j,t; 95 for(i=0;i<m;i++) 96 { 97 scanf("%d",&j); 98 if(j==1) 99 { 100 int a,b; 101 scanf("%d%d",&a,&b); 102 if(a>b) 103 swap(a,b); 104 node ans=query(1,a,b); 105 printf("%d ",ans.dat); 106 } 107 else 108 { 109 int x,y; 110 scanf("%d%d",&x,&y); 111 update(1,x,y); 112 } 113 } 114 } 115 116 /* 117 5 3 118 1 2 -3 4 5 119 1 2 3 120 2 2 -1 121 1 3 2 122 */