jzoj 3431. 【GDOI2014模拟】网格

Description

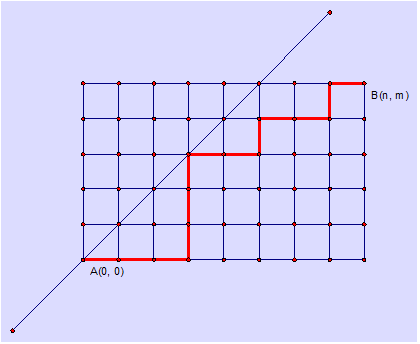
某城市的街道呈网格状，左下角坐标为A(0, 0)，右上角坐标为B(n, m)，其中n >= m。现在从A(0, 0)点出发，只能沿着街道向正右方或者正上方行走，且不能经过图示中直线左上方的点，即任何途径的点(x, y)都要满足x >= y，请问在这些前提下，到达B(n, m)有多少种走法。

Input

输入文件中仅有一行，包含两个整数n和m，表示城市街区的规模。

Output

输出文件中仅有一个整数和一个换行/回车符，表示不同的方案总数。

Data Constraint

50%的数据中，n = m，在另外的50%数据中，有30%的数据：1 <= m < n <= 100
100%的数据中，1 <= m <= n <= 5 000

Solution

首先，我们不考虑这条线的情况，则从(0,0)走到(n,m)的方案数则为(C_{m+n}^{m})
而我们现在只需要考虑非法的情况
因为不能超过y=x的直线，所以其实相当于不能碰到y=x+1这条线
做出(n,m)关于y=x+1的对称点M
则M(m-1,n+1)
从(0,0)走到(n,m)的非法方案相当于从 (0,0)走到M的方案，即(C^{m-1}_{n+m})
则答案则为

[ans=C_{m+n}^{m}-C_{m+n}^{m-1} ]

[=frac{(m+n)!}{m! imes n!}-frac{(m+n)!}{(m-1)! imes (n+1)!} ]

[=frac{(m+n)! imes (n+1)}{m! imes (n+1)!}-frac{(m+n)! imes m}{m! imes (n+1)!} ]

[=frac{(m+n)! imes (n+1-m)}{m! imes (n+1)!} ]

[=frac{(n+2) imes (n+3) imes... imes(m+n) imes (n+1-m)}{m!} ]

答案过大，要高精度处理
作者不会高精度除高精度，所以直接从2~m一个个的除
友情提示：高精度不压位会T飞，请慎重考虑

Code

#include <cstdio>
#define MO 1000000000
using namespace std;
int n,m,i,x;
long long a[100001],b[100001],c[100001];
void cheng(int w)
{
    int t=w,x;a[0]=0;
    while (t)
    {
        a[++a[0]]=t%MO;
        t/=MO;
    }
    for (int i=1;i<=c[0];i++)
    {
        x=0;
        for (int j=1;j<=a[0];j++)
            {
                b[i+j-1]+=c[i]*a[j]+x;
                x=b[i+j-1]/MO;
                b[i+j-1]%=MO;
            }
        b[i+a[0]]=x;
    }
    c[0]+=a[0];
    if (!b[c[0]]) c[0]--;
    for (int i=1;i<=c[0];i++)
        c[i]=b[i],b[i]=0;
}
void chu(int w)
{
    long long t=0,x=0;
    for (int i=c[0];i>=1;i--)
    {
        t=t*MO+c[i];
        c[i]=t/w;
        t=t%w;
    }
    while (!c[c[0]])c[0]--;
}
int main()
{
    scanf("%d%d",&n,&m);
    c[1]=n+2;c[0]=1;
    for (i=n+3;i<=n+m;i++)
    {
        cheng(i); 
    }
    cheng(n-m+1);
    for (i=2;i<=m;i++)
    {
    	chu(i);
    }
    printf("%lld",c[c[0]]);
    for (i=c[0]-1;i>=1;i--)
    {
        printf("%09lld",c[i]);
    }
}