使用
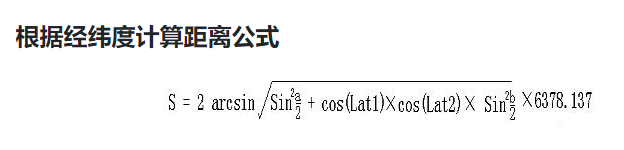
对上面的公式解释如下:
- Lung1 Lat1表示A点经纬度, Lung2 Lat2表示B点经纬度;
- a=Lat1 – Lat2 为两点纬度之差 b=Lung1 -Lung2 为两点经度之差;
- 6378.137为地球半径,单位为千米;
- 计算出来的结果单位为千米,若将半径改为米为单位则计算的结果单位为米。
- 计算精度与谷歌地图的距离精度差不多,相差范围在0.2米以下。
参数说明:
lng:经度
lat:纬度
地球半径:6378.137(千米)
一般地图上显示的坐标顺序为,纬度在前(范围-90 ~ 90),经度在后(范围-180 ~ 180)
使用(计算直线距离):
这种计算方式一般都是直线距离
sql语句:
SELECT *, 6378.138 * 2 * ASIN( SQRT( POW( SIN( ( '.$lat.' * PI() / 180 - lat * PI() / 180 ) / 2 ), 2 ) + COS('.$lat.' * PI() / 180) * COS(lat * PI() / 180) * POW( SIN( ( '.$lng.' * PI() / 180 - lng * PI() / 180 ) / 2 ), 2 ) ) ) *1000 AS distance FROM distance ORDER BY distance ASC
JS:
/** * 转换弧度 * @param d * @returns {number} */ function getRad(d){ var PI = Math.PI; return d*PI/180.0; } /** * 根据经纬度计算两点间距离 * @param lng1 * @param lat1 * @param lng2 * @param lat2 * @returns {number|*} * @constructor */ function CoolWPDistance(lng1,lat1,lng2,lat2){ var f = getRad((lat1 + lat2)/2); var g = getRad((lat1 - lat2)/2); var l = getRad((lng1 - lng2)/2); var sg = Math.sin(g); var sl = Math.sin(l); var sf = Math.sin(f); var s,c,w,r,d,h1,h2; var a = 6378137.0;//The Radius of eath in meter. var fl = 1/298.257; sg = sg*sg; sl = sl*sl; sf = sf*sf; s = sg*(1-sl) + (1-sf)*sl; c = (1-sg)*(1-sl) + sf*sl; w = Math.atan(Math.sqrt(s/c)); r = Math.sqrt(s*c)/w; d = 2*w*a; h1 = (3*r -1)/2/c; h2 = (3*r +1)/2/s; s = d*(1 + fl*(h1*sf*(1-sg) - h2*(1-sf)*sg)); if(s >= 1000 && s <= 99000){ var kilometer = s/1000; s = kilometer.toFixed(1) + 'km'; }else if(s > 99000){ s = '>99km'; }else{ s = Math.round(s) + 'm'; } // s = s/1000; // s = s.toFixed(2);//指定小数点后的位数。 return s; }
Java
第一步:添加Maven依赖
<dependency> <groupId>org.gavaghan</groupId> <artifactId>geodesy</artifactId> <version>1.1.3</version> </dependency>
第二步:代码实现
public class DistanceUtil { public static void main(String[] args) { System.out.println("经纬度距离计算结果:" + getDistance(109.371319, 22.155406, 108.009758, 21.679011) + "米"); } public static double getDistance(double longitudeFrom, double latitudeFrom, double longitudeTo, double latitudeTo) { GlobalCoordinates source = new GlobalCoordinates(latitudeFrom, longitudeFrom); GlobalCoordinates target = new GlobalCoordinates(latitudeTo, longitudeTo); return new GeodeticCalculator().calculateGeodeticCurve(Ellipsoid.Sphere, source, target).getEllipsoidalDistance(); } }
GPS,经度,纬度,距离在线计算器:
https://www.osgeo.cn/app/s1884
http://www.box3.cn/page/lbs.html
算法实现
问题描述
给定一个景点的经纬度,给定距离,给定形状,判断其它点是否在某个区域内:
圆形方案
使用通用的地球上两点距离函数,圆形只需要判断距离,正方形需要计算两次距离(指定经度与景点的经度一样,计算是否在范围内,然后指定纬度与景点的纬度一样,计算是否在范围内,如果都在范围内,则代表该点在景区范围内),其它形状基于这个基础类推
距离函数
Scala实现方式:
/** * Created on 2020/05/15. * * 求地球上两点间的距离 返回的是 double 格式的 km * 第一点经纬度为(lat1,lng1),第二点经纬度为(lat2,lng2),地球平均半径R=6378.137 * 按照0度经线的基准,东经取经度的正值(Longitude),西经取经度负值(-Longitude),北纬取90-纬度值(90- Latitude),南纬取90+纬度值(90+Latitude), * 则经过上述处理过后的两点被计为(MLon1, MLat1)和(MLon2, MLat2)。那么根据三角推导,可以得到计算两点距离的如下公式: * C = sin(MLat1)*sin(MLat2)*cos(MLon1-MLon2) + cos(MLat1)*cos(MLat2),Distance = R*Arccos(C)*Pi/180 * 如果仅对经度作正负的处理,而不对纬度作90-Latitude(假设都是北半球,南半球只有澳洲具有应用意义)的处理,那么公式将是: * C = sin(LatA)*sin(LatB) + cos(LatA)*cos(LatB)*cos(MLonA-MLonB),Distance = R*Arccos(C)*Pi/180 * 三角函数的输入和输出都采用弧度值,那么公式还可以写作: * C = sin(Lat1*Pi/180)*sin(Lat2*Pi/180) + cos(Lat1*Pi/180)*cos(Lat2*Pi/180)*cos((MLon1-MLon2)*Pi/180),Distance = R*Arccos(C)*Pi/180 * rad()函数求弧度,Distance()函数求距离 * * 结果验证工具地址 http://www.storyday.com/wp-content/uploads/2008/09/latlung_dis.html */ def distance(lat1: Double, lng1: Double, lat2: Double, lng2: Double): Double = { val EARTH_RADIUS = 6378.137 val radLat1 = rad(lat1) val radLat2 = rad(lat2) val a = rad(lat1) - rad(lat2) val b = rad(lng1) - rad(lng2) val distance = EARTH_RADIUS * 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2) + Math.cos(radLat1) * Math.cos(radLat2) * Math.pow(Math.sin((b) / 2), 2))) // printLog.debug("lat1: " + lat1 + " lng1: " + lng1 + " lat2: " + lat2 + " lng2: " + lng2) printLog.debug("distance:" + distance) distance }
不规则图形方案
scala实现函数:使用现成的算法PNPoly即可实现
/** * 多点位置判断算法 判断一个坐标点是否在不规则多边形内部 * * * 在 GIS(地理信息管理系统)中,判断一个坐标是否在多边形内部是个经常要遇到的问题。乍听起来还挺复杂。 * 根据 W. Randolph Franklin 提出的 PNPoly (http://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html) 算法,只需区区几行代码就解决了这个问题: * * * 针对每一个点,算法遍历多边形相邻的每两个顶点(即一条边),假如待判断点满足以下两个条件即改变点是否在多边形内的状态标识c: * 待判断点的Y坐标在点i和点j的Y坐标范围之内 * 待判断点的X坐标在点i和点j连线之下 * 遍历所有的边之后假如以上两个条件同时满足奇数次则该带判断点位于多边形之内,否则位于多边形之外。 * 算法复杂度为O(n),其中n为多边形的顶点个数。 * * @param vertexes * @param testPoint * @return */ def pNPoly(vertexes: Array[LocationPoint], testPoint: LocationPoint): Boolean = { var flag = false var flag0 = false var flag1 = false var flag2 = false var flag3 = false var j = vertexes.length - 1 val loop = new Breaks loop.breakable { for (i <- 0 until vertexes.length) { if (i != 0) { j = i - 1 } if ((vertexes(i).lat == testPoint.lat) && (vertexes(i).long == testPoint.long)) { flag0 = true } if (((vertexes(i).lat - testPoint.lat) * (vertexes(i).long - testPoint.long) * (vertexes(j).lat - testPoint.lat) * (vertexes(j).long - testPoint.long) == 0) && (((vertexes(i).lat > testPoint.lat) != (vertexes(j).lat > testPoint.lat)) && ((vertexes(i).long > testPoint.long) != (vertexes(j).long > testPoint.long)))) { flag1 = true } if (((vertexes(i).lat - testPoint.lat) * (vertexes(i).long - testPoint.long) * (vertexes(j).lat - testPoint.lat) * (vertexes(j).long - testPoint.long) != 0) && ((vertexes(i).lat - testPoint.lat) / (vertexes(i).long - testPoint.long) == (vertexes(j).lat - testPoint.lat) / (vertexes(j).long - testPoint.long))) { flag2 = true } if (((vertexes(i).lat > testPoint.lat) != (vertexes(j).lat > testPoint.lat)) && (testPoint.long < (vertexes(j).long - vertexes(i).long) * (testPoint.lat - vertexes(j).lat) / (vertexes(j).lat - vertexes(i).lat) + vertexes(i).long)) { flag3 = true } flag = flag0 || flag1 || flag2 || flag3 if (flag) { loop.break } } } flag }
在运用该算法之前,有个优化方案,就是先进行最小外接矩形范围判断,如果不在最小外接矩形中,则直接跳过
if (p.x < minX || p.x > maxX || p.y < minY || p.y > maxY) { // 点在多边形之外的实现 }
首先判断点是否在多边形的最小外接矩形之内,该步骤不是必须的,但是可以有效避免不必要的计算。
判断点是否在多边形内算法实现
PNPoly
PNPoly是由W. Randolph Franklin提出的一种在二维空间较为高效地判断点是否在多边形内的算法,算法具有很好的通用性,对凸多边形、凹多边形以及含有空洞的多边形均适用。
最小外接矩形范围判断

if (p.x < minX || p.x > maxX || p.y < minY || p.y > maxY) { // 点在多边形之外 }
首先判断点是否在多边形的最小外接矩形之内,该步骤不是必须的,但是可以有效避免不必要的计算。
核心算法

int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy) { int i, j, c = 0; for (i = 0, j = nvert-1; i < nvert; j = i++) { if ( ((verty[i]>testy) != (verty[j]>testy)) && (testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) ) c = !c; } return c; }
针对每一个点,算法遍历多边形相邻的每两个顶点(即一条边),假如待判断点满足以下两个条件即改变点是否在多边形内的状态标识c:
- 待判断点的Y坐标在点i和点j的Y坐标范围之内
- 待判断点的X坐标在点i和点j连线之下
遍历所有的边之后假如以上两个条件同时满足奇数次则该带判断点位于多边形之内,否则位于多边形之外。
算法复杂度为O(n),其中n为多边形的顶点个数。
算法主页: PNPoly
相关出版物:Haines, Eric, “Point in Polygon Strategies,” Graphics Gems IV, ed. Paul Heckbert, Academic Press, p. 24-46, 1994.
基于扫描填充多边形的方法
若针对同一多边形有大量的点需要判断是否在该多边形的话上述方法计算量将会很大,可以借助计算机图形学中的多边形填充方法,采用影像辅助判断点是否在多边形内,基于voronoi图的影像镶嵌(正射影像制作)是该方法典型的运用。
首先计算多边形的最小外接矩形,采用openCV绘制一张与外接矩形大小的黑色图像(图像分辨率可自定义,为适应之后的填充算法创建的影像的大小在扫描方向上需多加1个像素),在图像上绘制多边形的边。
image = cv::Mat::zeros(height,width,CV_8UC1);
line(image,pointi,pointj,255);
绘制多边形边
对上面的影像进行填充:

for (int i = 0; i < height; i++) { int trans_count(0); bool is_in_pologon(false); int trans_index(0); for (int j = 0; j < width-1; j++) { //cv::Vec3b a = image.at<cv::uchar>(i,j); if (image.at<cv::uchar>(i,j)==white_pixl&&image.at<cv::uchar>(i,j+1)!=white_pixl) { is_in_pologon = !is_in_pologon; trans_index = j; trans_count++; } if (is_in_pologon) { image.at<cv::uchar>(i,j) = 255; } } if (is_in_pologon) { image.at<cv::uchar>(i,width-1); } if (trans_count == 1) { for (int j = width-1; j > trans_index; j--) { image.at<cv::uchar>(i,j) = 0; } } }
扫描填充影像将待判断点的坐标换算到影像上若得到相应的像素值为255则该点在这个多边形之内,若得相应像素值为0则该点在多边形外。
