AGC 002E.Candy Piles(博弈论)

题目链接

---

(Description)

给定(n)堆糖，数量分别为(a_i)。Alice和Bob轮流操作。每次可以吃掉最多的一堆，也可以每堆各吃掉一个。无法操作的人输，求谁能赢。
(nleq10^5, a_ileq10^9)。

(Solution)

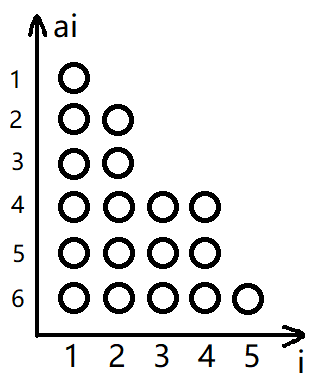
画这图累死了= = 虽然确实有点丑
假设有(5)堆糖，把它画成这样。我们发现每次操作就是拿掉最左边一列或最下边的一行。那么可以看成，初始在((1,1))，每次向右或向上走一步。
考虑求(SG)。边界位置的(SG)值显然为(0)，且(SG)只有(01)两种取值表示胜负。其余位置的(SG)都可以求出，但是复杂度会炸。
打表可以发现，除去最边上一层，同一条副对角线上的位置的(SG)值是相同的，即(sg(x,y)=sg(x+1,y+1))。
考虑若(sg(x+1,y+1)=1)，((x,y))的后继的后继会有((x+1,y+1))这一必胜态，所以(sg(x,y)=1)；若(sg(x+1,y+1)=0)，则((x,y))的后继存在必败态的后继，所以(sg(x,y)=0)。
然后我们就可以找第一个满足(i+1>A_{i+1})的位置((i,i))，求((i,i))的(SG)值，即右边上边各有多少个位置有糖即可。

这个结论是很常用的结论：同一条对角线上的(SG)值相同。

---

//8ms	896KB
#include <cstdio>
#include <cctype>
#include <algorithm>
#include <functional>
#define gc() getchar()
#define MAXIN 300000
//#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef long long LL;
const int N=1e5+5;

int A[N];
char IN[MAXIN],*SS=IN,*TT=IN;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-48,c=gc());
	return now;
}

int main()
{
	const int n=read();
	for(int i=1; i<=n; ++i) A[i]=read();
	std::sort(A+1,A+1+n,std::greater<int>());
	for(int i=1; i<=n; ++i)
		if(i+1>A[i+1])
		{
			int ans=0;
			for(int j=i+1; A[j]==i; ++j) ans^=1;
			ans|=A[i]-i&1;
			puts(ans?"First":"Second");
			return 0;
		}

	return 0;
}