0. 弧度制——自然角度制
相信大多数人都知道,角度制是指将周角平均分成360份,每一份称为1度的角度制.
然而你会不会有以下的疑问:
凭什么我定义分成360份就是1度?分成720份怎么了?
然而真相是你定义分成多少份都没问题,甚至是像343.7321这样奇怪的数字.
但是为了保持数学的纯粹,我们一直在求索一种可以"自然"地表示角度的方法.
那么,人们的努力有没有成果呢?
有!请看:
1. 定义
引入弧度的原因上面已经解释了,那么,引入弧度制:
$$ heta=frac{l}{r}$$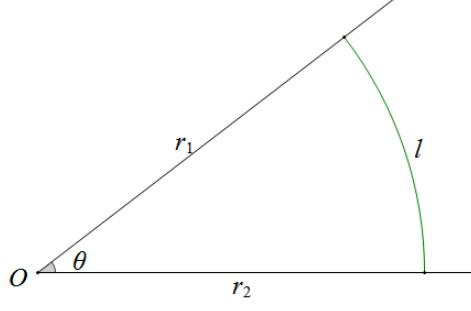
其中$l$为弧长,$r$为半径.
所以
$45 quad deg=pi/4 quad rad$
$90 quad deg=pi/2 quad rad$
$180 quad deg=pi quad rad$
$360 quad deg=2pi quad rad$
2. 单位
为了表示弧度制,有些时候会写上$rad$;
然而有些情况下是不加任何东西的
可不可以加($m/m$)(手动滑稽)
3. 弧度制的用处
需要用到角的地方就能用弧度制啊qwq
4. 一个弧度制明显优于角度制的地方
原谅我用了这个长的要死的标题...
然而你可能都想不到...
正弦波(滑稽)
弧度制下是酱的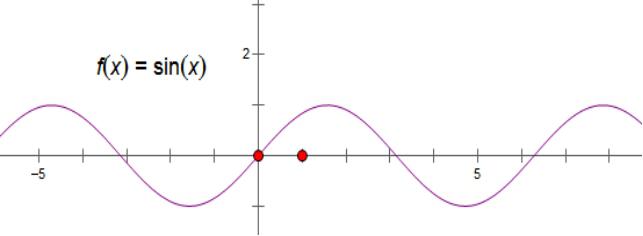
很正常吧QAQ
然鹅...
角度制下则是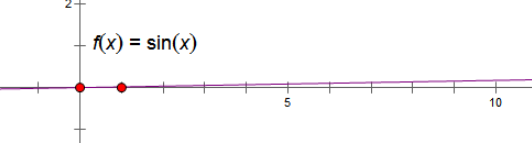
emm...
自己体会吧
5. 结语
弧度制无论是在高中数学还是高中物理都是强制要求
(你再写180 90老师会认为是弧度...)
所以弧度制的重要性是不言而喻的.
但从角度到弧度是一个飞跃,也是一个坎儿.
多使用,习惯了就会体会到它的美感.
