4-1
算法的复杂性有时间复杂性和空间复杂性之分。
4-2
若存在两个正的常数c和n0,对于任意n≥n0,都有T(n)≤c×f(n),则称T(n)= Ω (f(n))。
4-3
用贪心算法求解的问题一般具有两个重要性质是:
贪心原则和最优子结构性质。
4-4
分支限界法采用
深度
优先的方式搜索解空间,回溯法采用
广度
优先的方式搜索解空间。
4-5
通常,
贪心算法、分支限界、回溯的求解策略是自顶向下求解,
动态规划是自底向上的递推求解。
4-6
回溯法搜索解空间树时,常用的两种剪枝函数为
约束函数和限界函数
4-7
分支限界法主要有
队列式 分支限界法和 优先队列式 分支限界法。
5-1
如下程序的功能是求解n后问题,请将程序补充完整。(每空2分,共10分)
#include <iostream.h>
#include <math.h>
int n,count,*x;
void Swap(int& a,int &b){
int t=a;a=b;b=t; }
bool Check(int i){ //检查当前第i个皇后的放法是否可行
for (int k=1;k<i;k++)
if (
(a[i]==a[j])||(abs(a[i]-a[j])==i-j)
) return false;
else return true
;
}
void Output(){
//以表格的形式输出一个解(x1,x2,…,xn),皇后所在的行列位置为“Q”,其它位置输出“_”。
count++;
for ( int i=1;i<=n;i++){
for (j=1;j<=n;j++)
if (x[i]==j) cout<<" Q";
else cout<<"_";
cout<<endl;
}
}
void Queen(int i){
if (i>n)Output();
else
for (int j=i;j<=n;j++){
x[i] = j
;
if (check(i))
Queen(i+1)
;
Swap(x[i],x[j]);
}
}
void main(){
cout<<endl<<"Please input n="; cin>>n;
x=new int [n+1];
for (int i=1;i<=n;i++)
x[i]=-1
;
count=0;
Queen(1);
cout<<endl<<"Total ="<<count<<endl;
delete[]x;
}
7-1 找第k小的数 (20分)
设计一个平均时间为O(n)的算法,在n(1<=n<=1000)个无序的整数中找出第k小的数。
提示:函数int partition(int a[],int left,int right)的功能是根据a[left]a[right]中的某个元素x(如a[left])对a[left]a[right]进行划分,划分后的x所在位置的左段全小于等于x,右段全大于等于x,同时利用x所在的位置还可以计算出x是这批数据按升非降序排列的第几个数。因此可以编制int find(int a[],int left,int right,int k)函数,通过调用partition函数获得划分点,判断划分点是否第k小,若不是,递归调用find函数继续在左段或右段查找。
输入格式:
输入有两行:
第一行是n和k,0<k<=n<=10000
第二行是n个整数
输出格式:
输出第k小的数
输入样例:
在这里给出一组输入。例如:
10 4
2 8 9 0 1 3 6 7 8 2
输出样例:
在这里给出相应的输出。例如:
2
//找第k小的数
#include <iostream>
using namespace std;
int partition(int a[], int left, int right) {
//将数组a的第left到right个元素进行划分
int x = a[left];
while (left < right){//采用快排策略
while (left < right && a[right] >= x) right--;
a[left] = a[right];
while (left < right && a[left] <= x) left++;
a[right] = a[left];
}
a[left] = x;
return left;
}
int find(int a[], int left, int right, int k) {
//在数组a的第left到right中寻找第k小的数
int pos = partition(a, left, right);
if (k - 1 == pos) cout << a[k - 1];
else if (k - 1 < pos)//判断下一次划分在哪一区间进行
find(a, left, pos - 1, k);
else find(a, pos + 1, right, k);
return 0;
}
int main() {
int n, k;
cin >> n >> k;
int a[1000];
for (int i = 0; i < n; i++)
cin >> a[i];
find(a, 0, n - 1, k);
return 0;
}
7-2 装箱问题 (10分)
假设有N项物品,大小分别为s1 、s2 、…、si 、…、sN ,其中si 为满足1≤si ≤100的整数。要把这些物品装入到容量为100的一批箱子(序号1-N)中。装箱方法是:对每项物品, 顺序扫描箱子,把该物品放入足以能够容下它的第一个箱子中。请写一个程序模拟这种装箱过程,并输出每个物品所在的箱子序号,以及放置全部物品所需的箱子数目。
输入格式:
输入第一行给出物品个数N(≤1000);第二行给出N个正整数si (1≤si ≤100,表示第i项物品的大小)。
输出格式:
按照输入顺序输出每个物品的大小及其所在的箱子序号,每个物品占1行,最后一行输出所需的箱子数目。
输入样例:
8
60 70 80 90 30 40 10 20
输出样例:
60 1
70 2
80 3
90 4
30 1
40 5
10 1
20 2
5
#include <stdio.h>
#include <stdlib.h>
int main()
{
int n,top = 1,i,j,flag;
int a[1001];
int b[1001];
scanf("%d",&n);
for(i = 0;i < n;i++)
{
scanf("%d",&a[i]);
b[i] = 100;
}
if(n == 1)
{
printf("%d %d
%d
",a[0],top,top);
return 0;
}
for(i = 0;i < n;i++)
{
flag = 0;
for(j = 1;j <= top;j++)
{
if(b[j] >= a[i])
{
b[j] -= a[i];
flag =1;
printf("%d %d
",a[i],j);
break;
}
}
if(!flag)
{
top++;
b[top] -= a[i];
printf("%d %d
",a[i],top);
}
}
printf("%d
",top);
return 0;
}
7-3 0-1背包 (20分)
给定n(n<=100)种物品和一个背包。物品i的重量是wi,价值为vi,背包的容量为C(C<=1000)。问:应如何选择装入背包中的物品,使得装入背包中物品的总价值最大? 在选择装入背包的物品时,对每种物品i只有两个选择:装入或不装入。不能将物品i装入多次,也不能只装入部分物品i。
输入格式:
共有n+1行输入: 第一行为n值和c值,表示n件物品和背包容量c; 接下来的n行,每行有两个数据,分别表示第i(1≤i≤n)件物品的重量和价值。
输出格式:
输出装入背包中物品的最大总价值。
输入样例:
在这里给出一组输入。例如:
5 10
2 6
2 3
6 5
5 4
4 6
输出样例:
在这里给出相应的输出。例如:
15
#include<iostream>
using namespace std;
int main(){
int n,c;
cin>>n>>c;
int w[105];
int v[105];
int dp[105][1005]={};
for(int i=1;cin>>w[i]>>v[i];i++);
for(int i=1;i<=n;i++){
for(int j=1;j<=c;j++){
dp[i][j]=dp[i-1][j];
if(j>=w[i])
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
}
}
cout<<dp[n][c];
}
8-1 算法复杂度分析题 (6分)
请分别给出你求解7-1、7-2、7-3所设计算法的时空复杂度。
时间复杂度都为O(n^2)
8-2 算法应用题 (6分)
采用启发式搜索A*算法求解以下八数码难题,其中(a)为初始状态,(b)为目标状态,给出求解思路及估价函数。

求解思路:
对应网址
用启发式搜索算法求解,A* 算法。
定义六个结构体:
九宫格的各个数字,
OPEN结点,
OPEN表,
CLOSED结点,
CLOSED表,
求解路径。
自定义函数:
初始化九宫格;
判断两个九宫格是否一致;
求某结点的hx值,即与目标结点九宫格不一样的元素个数;
对OPEN表按照估价函数值的大小从小到大排序;
判断某九宫格是否与OPEN表中某结点相同;
判断某九宫格是否与CLOSED表中某结点相同;
将一个九宫格中的数字全部复制到另一个九宫格中;
求OPEN表中某结点的扩展结点;
删除OPEN表中第一个结点;
计算估价函数值并赋值;
以矩阵形式打印九宫格;
打印求解最终路径;
启发式搜索函数寻找求解路径。
估价函数:
/*********先定义所需要的结构体*********/
typedef struct{
int num[3][3]; //九宫格数字
}Squared; //九宫格
typedef struct{
Squared stateself; //九宫格
int dx; //结点在搜索树中的深度
int hx; //结点对应九宫格与目标九宫格不一样的元素个数
int fx; //估价函数fx=dx+hx
}Open; //OPEN结点
//求某结点的hx值,即与目标结点九宫格不一样的元素个数
int GetHx(Squared a,Squared end){
int count=0;
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
if(a.num[i][j]!=end.num[i][j])
count++;
}
}
return count;
}
/**********计算估价函数值并赋值**********/
void CalEvaluate(Open &op,Open pare,Squared end){
op.dx=pare.dx+1; //求dx
op.hx=GetHx(op.stateself,end); //求hx
op.fx=op.dx+op.hx; //求fx
}
8-3 最长公共子序列问题(LCS) (16分)
最长公共子序列问题(LCS) 下面的公式是最长公共序列子问题的递归关系式,Ci,j 表示序列Xi和Yj的最长公共子序列的长度,其中Xi={x1,x2,x3,…,xi},Yj={y1,y2,y3,…,yj}, bi,j 记录了Ci,j 的值是由哪一个子问题的解产生。
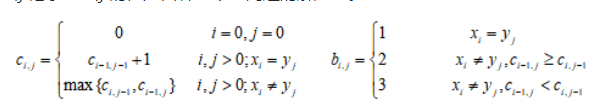
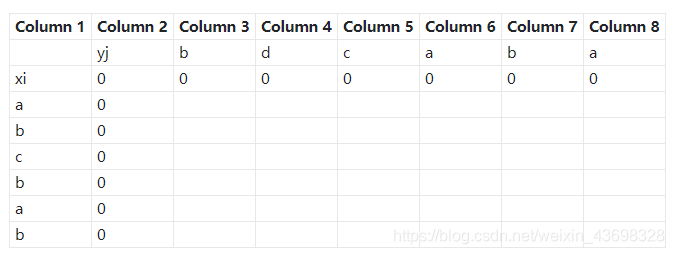
已知 X=(a, b, c ,b, d, a, b),Y=(b, d, c, a, b, a) (1)请根据以上动态规划方程给出C表和B表,下表为C表、B表参考格式,请通过上传文件、图片或者插入图片方式提交C表及B表;
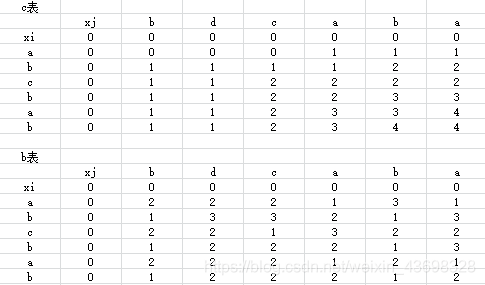
(2)根据表C和B的值,X与Y构成的最长公共子序列的长度为多少?
最大长度为4
(3)请给出X与Y构成的最长公共子序列?
公共子序列为bcba