【SInGuLaRiTy-1025】 Copyrights (c) SinGuLaRiTy 2017. All Rights Reserved.
[POJ 1905] 棍的膨胀 (Expanding Rods)
题目描述
已知一根长为L的细棍被加热了n摄氏度,那么其新的长度为L'=(1+n*C)*L。中间的C是热膨胀系数。
当一根细棍被夹在两面墙中间然后被加热,它会膨胀,其形状会变成一个弧,而原来的细棍(加热前的细棍)就是这个弧所对的弦。
你的任务是计算出弧的中点与弦的中点的距离。

输入
包含多组数据(每组占一行)。每一行包含三个非负数:细棍的长度,温度的变化值和细棍材料的热膨胀系数C。输入数据保证细棍不会膨胀超过自己的一半。
输入数据以三个连续的-1结尾。
输出
对于每一组数据,输出计算的距离,答案保留三位小数。
样例数据
| 样例输入 | 样例输出 |
1000 100 0.0001
15000 10 0.00006
10 0 0.001
-1 -1 -1
|
61.329
225.020
0.000
|
解析
直接二分高度,通过高度和弦长推出半径,再算角度,最后与实际的弧长进行比较,并最后进行调整。
这种算法的好处有以下几点;
1.使用相交弦定理,求出半径
2,只在求sita时使用了一次反三角函数,不像其他的算法,反复的求三角正弦,余弦啊各种·····尽量保留了精度。
3,突破以往的二分模式,并不求关于高度的calcu表达式,而是间接利用,以判断大小
4,最后,我觉得最神奇的是大神在复杂的题意下,找到了一个非常简洁的单挑函数:依题长度增加做多不过一半,也就是其形成的扇形组最大不过是半圆,那么在弦长一定的时候,给一个弧高就可以确定一个圆,进而可以确定这段弧长。
<Matchperson的分析写的很棒,这里粘一下>
一道典型的二分题目,我们会想到直接二分答案dis,然后就可以计算出这个弧所在的圆的半径,紧接着就可以求出弧长。用求出的弧长与真正的弧长做对比来确定下一次二分的范围。
但是有个问题,怎么保证算出的弧长满足单调性?可以yy一下得到。
1.dis小的时候:
2.dis大的时候:
在木棍原长度不变的情况下,dis越大,显然木棍越膨胀,所以弧长也就越大,满足单调性。
满足了单调性之后,我们就可以安心二分了,这里再详细说明一下如何求弧长:
根据勾股定理,我们知道(R-dis)^2+(len/2)^2=R^2,所以:
R^2-2*R*dis+dis^2+len^2/4=R^2
2*R*dis=dis^2+len^2/4
R=(dis+len^2/4/dis)/2
根据len’=2*θ*R=2*acos((R-dis)/R)*R(acos表示反三角函数,即知道cos值求角度(弧度制)),就可以得到弧长。
二分的范围:弧最多是半圆,所以dis最多是len/2。
特殊:当len=0或n=0或C=0时,答案就是0,最好特判掉。否则可能会造成被0除错误。
Code
#include<cstdio> #include<cmath> #include<cstring> using namespace std; #define eps 1e-4 double l,c,ls,n,r,sita; double solve(double a,double b) { double left,right,mid; left=a; right=b; while(left+eps<right) { mid=(left+right)/2; r=l*l/8/mid+mid/2; sita=2*asin(l/2/r); if(sita*r>=ls) right=mid; else left=mid; } return left; } int main() { while(~scanf("%lf%lf%lf",&l,&n,&c)) { if(l<0||n<0||c<0)break; ls=l*(1+n*c); printf("%.3f ",solve(0,l/2)); } return 0; }
[POJ 1836] 士兵站队 (Alignment)
题目描述
在军队中,一个团是由士兵组成的。在早晨的检阅中,士兵们在长官面前站成一行。但长官对士兵们的队列并不满意。士兵们的确按照他们的编号由小到大站成一列,但并不是按高度顺序来站的。于是,长官让一些士兵出列,其他留在队里的士兵没有交换位置,变成了更短的一列。这个队列满足一下条件:队伍里的每一个士兵都至少可以看见整个队伍的最前方或最后方,(如果一个士兵要看到队伍的最前方或最后方,那么在他的前方或后方,都没有比他高的人)。
现在按顺序给出一个队列里的每个士兵的身高,计算出若要形成满足上述条件的队列,长官至少需要让多少士兵出列。
输入
输入数据的第一行,包含一个整数n,表示原队列里士兵的数量。第二行,包含n个浮点数(最多有五位小数),第i个浮点数表示队列中编号为i的士兵的身高hi。
其中:2 <= n <= 1000 ,且身高hi的取值范围[0.5,2.5]。
输出
包含一个整数,表示需要出列的最少士兵数。
样例数据
| 样例输入 | 样例输出 |
8
1.86 1.86 1.30621 2 1.4 1 1.97 2.2
|
4
|
解析
这道题嘛,就是让队列里最少的士兵出列,使队列变成这么一个样子,如图-1。由于要求最少出列人数,也就是保留最多人数,于是这道题就有了求最长上升子序列的DP做法。对第i个人,计算1~i的最长上升序列(长度为l)与i+1~n的最长下降序列(长度为d),对所有的i,取l+d的最大值max。答案即为n-max。二分+枚举也可求解。

图-1
Code
#include<cstdio> #include<cstdlib> #include<iostream> #include<algorithm> #include<cstring> #include<cmath> using namespace std; int n; double num[1111]; double up[1111]; double down[1111]; const int inf=(1<<31)-1; int b1(double ss,int Left,int Right) { int L=Left;int R=Right; int mid; while(L<R) { mid=(L+R)>>1; if(up[mid]>ss) { R=mid; mid=(L+R)>>1; } else if(up[mid]==ss) { return mid; } else { L=mid+1; mid=(L+R)>>1; } } return R; } int b2(double ss,int Left,int Right) { int L=Left;int R=Right; int mid; while(L<R) { mid=(L+R)>>1; if(down[mid]<ss) { R=mid; mid=(L+R)>>1; } else if(down[mid]==ss) { return mid; } else { L=mid+1; mid=(L+R)>>1; } } return R; } int main() { int ans=0; scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%lf",&num[i]); for(int i=1;i<=n;i++) { memset(up,0,sizeof(up)); memset(down,0,sizeof(down)); int lisnum=1; up[0]=-1; for(int j=1;j<=i;j++) { int index=b1(num[j],0,lisnum); if(index==lisnum) lisnum++; up[index]=num[j]; } int ldsnum=1; down[0]=inf; for(int j=i+1;j<=n;j++) { int index=b2(num[j],0,ldsnum); if(index==ldsnum) ldsnum++; down[index]=num[j]; } lisnum--;ldsnum--; ans=max(ans,lisnum+ldsnum); } printf("%d ",n-ans); }
[POJ 3714] 突袭 (Raid)
题目描述
给出A、B两个点集,每个集合包含N个点。现要求分别从两个点集中取出一个点,使这两个点的距离最小。
输入
输入的第一行包含一个整数T,表示样例个数。
接下来有T个样例,每个样例的第一行为一个整数N (1 ≤ N ≤ 100,000),表示每个组的点的个数
随后有N行,每行有两个整数X (0 ≤ X ≤ 1,000,000,000) and Y (0 ≤ Y ≤ 1,000,000,000),代表A组的各点的坐标。
再随后N行,每行有两个整数X (0 ≤ X ≤ 1,000,000,000) and Y (0 ≤ Y ≤ 1,000,000,000),代表B组的各点的坐标。
输出
对于每个样例,输出两点间最小的距离,保留3位小数。注意两个点必须来自两个不同的组。
样例数据
| 样例输入 | 样例输出 |
2
4
0 5
0 0
1 0
1 1
2 2
2 3
3 2
4 4
4
0 0
1 0
0 1
0 0
0 0
1 0
0 1
0 0
|
1.414
0.000
|
解析
无集合限制的求最近点对:
对所有点先按x坐标不减排序,对x进行二分,得到点集S1,点集S2,通过递归求得S1,S2的最小点对距离d1,d2;D=min{d1,d2};合并S1,S2:找到在S1,S2划分线左右距离为D的所有点,按y不减(不增也可以)排序;循环每个点找它后面6个点的最小距离;最后即求得最小点对距离。
这道题有集合限制嘛,把同一集合之间点的距离定为无穷大就行了。
Code
#include<cstdio> #include<algorithm> #include<cmath> #define INF 1<<30 using namespace std; long long x[200010],y[200010]; int orderx[200010],ordery[200010],n; double solve(int start,int end); bool cmpx(int i,int j) { if(x[i]<x[j]) return 1; else return 0; } bool cmpy(int i,int j) { if(y[i]<y[j]) return 1; else return 0; } double disx(int i,int j) { if(orderx[i]<n&&orderx[i]<n) return INF; else if(orderx[i]>=n&&orderx[i]>=n) return INF; else return sqrt((double)((x[orderx[i]]-x[orderx[j]])*(x[orderx[i]]-x[orderx[j]])+(y[orderx[i]]-y[orderx[j]])*(y[orderx[i]]-y[orderx[j]]))); } double disy(int i,int j) { if(ordery[i]<n&&ordery[j]<n) return INF; else if(ordery[i]>=n&&ordery[j]>=n) return INF; else return sqrt((double)((x[ordery[i]]-x[ordery[j]])*(x[ordery[i]]-x[ordery[j]])+(y[ordery[i]]-y[ordery[j]])*(y[ordery[i]]-y[ordery[j]]))); } double min(double a,double b){return a>b?b:a;} double min(double a,double b,double c) { return min(a,min(b,c)); } int main() { int T,i,j; scanf("%d",&T); while(T--) { scanf("%d",&n); for(i=0;i<2*n;i++) { scanf("%d%d",x+i,y+i); orderx[i]=ordery[i]=i; } sort(orderx,orderx+2*n,cmpx); printf("%.3lf ",solve(0,2*n-1)); } return 0; } double solve(int start,int end) { if(start+1==end) return disx(start,end); else if(start+2==end) return min(disx(start,start+1),disx(start,start+2),disx(start+1,start+2)); else { int mid=start+(end-start)/2; double d=min(solve(start,mid),solve(mid+1,end)); int t=0; for(int i=start;i<=end;i++) if(fabs((double)x[orderx[i]]-(double)x[orderx[mid]])<=d) ordery[t++]=orderx[i]; sort(ordery,ordery+t,cmpy); for(int i=0;i<t;i++) for(int j=i+1;j<min(end,i+6);j++) d=min(d,disy(i,j)); return d; } }
[POJ 3122] 分馅饼 (Pie)
题目描述
我过生日请了F个朋友来参加我的生日party。总共有N个馅饼,要把它们平均分给每个人(包括我),并且每个人只能从一块馅饼得到自己的那一份,并且分得的馅饼大小要一样,形状可以不一样,每块馅饼都是圆柱,高度一样。
输入
第1行:一个正整数,表示测试数据的组数。
在每一组数据中:第1行包含两个整数,N和F (1 ≤ N, F ≤ 10 000);第2行包含N个整数,表示每一个馅饼的半径。
输出
对于每一组数据,输出可能的最大体积。要求误差小于10^(-3),即至少保留四位小数。
样例数据
| 样例输入 | 样例输出 |
3
3 3
4 3 3
1 24
5
10 5
1 4 2 3 4 5 6 5 4 2
|
25.1327
3.1416
50.2655
|
解析
贪心的思想+二分。复杂度为O(nlogM),M为初始时的high-low。初始状态,上界high为每个人分得奶酪的体积sum,下界low = 0(或者是最小块的奶酪)。然后二分,每次的mid值为(low+high)/ 2,然后根据mid值(估计值)遍历n块奶酪,看看这个mid值能分给多少个人,如果份数大于等于f,表示mid偏小,low = mid,反之high = mid。
注意:这里的圆周率pi应该尽量精确,否则容易被卡精度。
Code
#include<cstdio> #include<cmath>
double pi=acos(-1.0); double sum,mid,le,ri,b[10000+11],max0;
int n,f,r;
double fl(double x) { int su=0; for(int i=0;i<n;i++) { su+=(int)(b[i]/x); } return su; }
int main() { int t; scanf("%d",&t); while(t--) { sum=0; scanf("%d %d",&n,&f); f++; for(int i=0;i<n;i++) { scanf("%d",&r); b[i]=r*r*pi; sum+=b[i]; } sum=sum/f; le=0.0; ri=sum; while(fabs(ri-le)>1e-6) { mid=(le+ri)/2; if(fl(mid)>=f) { le=mid; } else { ri=mid; } } printf("%.4f ",le); } }
[POJ 2366] 总和的圣礼 (Sacrament of the sum)
题目描述
从前,有一对感情破裂的兄弟。为了拯救他们之间的感情,兄弟两人每个人都准备了一些对于他们来说可以拯救他们之间感情的数字,这些数字可以拯救他们的感情吗?(若在两个列表中的分别存在一个数,它们的和为10000,则我们认为这些数字可以拯救他们之间的感情)。你的程序应该决定,是否有可能从两个整数列表选择这样两个数字,来拯救他们的感情。
输入
每堆数(共2堆)的输入格式如下:每堆数的第一行,包含一个整数N ( 1 <= N <= 50,000 ),表示当前列表中的数字的个数;接下来N行,每一行包含一个整数A ( -32767<= A <=32767 )。输入数据保证:第一堆数按照升序排列,第二堆数按照降序排列。
输出
如果能找到符合要求的两个数,就输出"YES",否则输出"NO"
样例数据
| 样例输入 | 样例输出 |
4
-175
19
19
10424
3
8951
-424
-788
|
YES
|
解析
由于两个数列都有序(连sort都不用),直接对一个列表进行枚举,对另一个列表进行二分查找就行了。
Code
#include<cstdio> #include<cstring> #include<cstdlib> #include<cmath> #include<algorithm> #include<iostream> using namespace std; int A[50000],B[50000]; int main() { int n1,n2,mid,Max,Min; scanf("%d",&n1); for(int i=0;i<n1;++i) scanf("%d",&A[i]); scanf("%d",&n2); for(int i=0;i<n2;++i) scanf("%d",&B[i]); for(int i=0;i<n1;++i) for(Min=0,Max=n2-1,mid=(Max+Min)/2;Min<=Max;mid=(Max+Min)/2) { if(A[i]+B[mid]==10000) { printf("YES"); return 0; } else if(A[i]+B[mid]>10000) Min=mid+1; else Max=mid-1; } printf("NO"); return 0; }
[POJ 3301] 德克萨斯之旅 (Texas Trip)
题目描述
在与Dick一天的旅行之后,Harry在自己SUV的车门上发现了几个奇怪的小孔。而当地的维修店只出售正方形的玻璃纤维修补材料。现在,我们把车门上的小孔当做位于平面上整数坐标的点,问: 至少要一块多大面积的正方形修补材料才能覆盖住所有的小孔?
输入
第一行包含一个整数T (T ≤ 30),表示有T组测试数据。
对于每一组数据,第一行包含一个整数n (n ≤ 30),表示有n个小孔。接下来有N行,每行两个整数X和Y,分别表示一个小孔的横坐标和纵坐标。输入数据保证每一个小孔距离原点(0,0)不超过500个单位距离。
输出
对于每一组数据,输出一个两位小数,表示正方形材料的最小面积。
样例数据
| 样例输入 | 样例输出 |
2
4
-1 -1
1 -1
1 1
-1 1
4
10 1
10 -1
-10 1
-10 -1
|
4.00
242.00
|
解析
刚开始看到题,以为正方形不会旋转,算算点的边界就行了,后来才发现: 如果正方形旋转起来,面积是有可能减小的。下面是正解: 为了便于计算,我们不让正方形旋转,而是让正方形边始终与坐标轴保持平行,让点旋转,三分点的旋转角度,范围[0,pi],每次旋转后统计横纵坐标最大差值 (计算边界) ,取个最大值即为当前角度对应的正方形边长 。

图-2
Code
#include<cstdio> #include<iostream> #include<algorithm> #include<cmath> using namespace std; #define eps 1e-12 #define pi acos(-1.0) #define maxn 33 struct node { double x,y; node spin(double a) { node ans; ans.x=x*sin(a)-y*cos(a); ans.y=x*cos(a)+y*sin(a); return ans; } }a[maxn],b[maxn]; int T,n; double cal(double x) { for(int i=0;i<n;i++)b[i]=a[i].spin(x); double x1,x2,y1,y2; x1=x2=b[0].x,y1=y2=b[0].y; for(int i=1;i<n;i++) x1=min(x1,b[i].x),x2=max(x2,b[i].x),y1=min(y1,b[i].y),y2=max(y2,b[i].y); return max(x2-x1,y2-y1); } int main() { scanf("%d",&T); while(T--) { scanf("%d",&n); for(int i=0;i<n;i++) scanf("%lf%lf",&a[i].x,&a[i].y); double l=0,r=pi,mid1,mid2,f1,f2; while(1) { mid1=(l+r)/2; mid2=(mid1+r)/2; f1=cal(mid1); f2=cal(mid2); if(abs(f1-f2)<eps) break; else if(f1<f2) r=mid2; else l=mid1; } printf("%.2f ",f1*f1); } return 0; }
[POJ 2503] 宝贝鱼翻译机 (Bablefish)
题目描述
你刚刚从滑铁卢(Waterloo)搬到了一个新的大城市。这里的人们都说着一种令人费解的外语方言。幸运的是,你有一本可以帮助你理解的词典。
输入
输入包含最多100,000条词典条目,接下来有一个空行,其次是最多100,000词的原始信息。
每一个词典条目包含用空格分开的两个字符串S1和S2,其中S1是译文,S2是原文。原始信息为多行,一行一个需要翻译的单词。
输入数据保证每一个单词的程长度不超过10个字符。
输出
对于每一个需要翻译的单词,输出翻译后的单词。若原始单词不存在在词典中,输出"eh"(不包含引号)。
样例数据
| 样例输入 | 样例输出 |
dog ogday
cat atcay
pig igpay
froot ootfray
loops oopslay
atcay
ittenkay
oopslay
|
cat
eh
loops
|
解析
从小到大排序,然后对于每个询问,二分查找。复杂度O(nlogn)。
Code
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; struct node { char s1[20],s2[20]; }a[100005]; int len; int cmp(node a,node b) { return strcmp(a.s2,b.s2)<0; } int main() { len=0; char str[50]; while(gets(str)) { if(str[0]=='�') break; sscanf(str,"%s%s",a[len].s1,a[len].s2); len++; } sort(a,a+len,cmp); while(gets(str)) { int l=0,r=len-1,mid,flag=1; while(l<=r) { int mid=(l+r)>>1; if(strcmp(str,a[mid].s2)==0) { printf("%s ",a[mid].s1); flag=0; break; } else if(strcmp(str,a[mid].s2)<0) r=mid-1; else l=mid+1; } if(flag) printf("eh "); } return 0; }
[POJ 3737] UmBasketella (UmBasketella)
题目描述
给定圆锥的表面积S,求这个圆锥的最大体积V,以及此时它的高h与底面半径r。
输入
输入数据中有多个测试点,每个测试点只包含一个实数 S, 代表圆锥的表面积。表面积 1≤S≤10000.
输出
对于每个测试点,输出应该包含三行:
第一行输出最大体积V;
第二行输出高h;
第三行输出底面半径r;
所有实数应该四舍五入到0.01。
样例数据
| 样例输入 | 样例输出 |
30
|
10.93
4.37
1.55
|
解析
枚举底面圆半径,算圆锥的体积。可以列出表达式,满足三分,因此可以三分枚举底面圆半径。
<三分查找>
概念
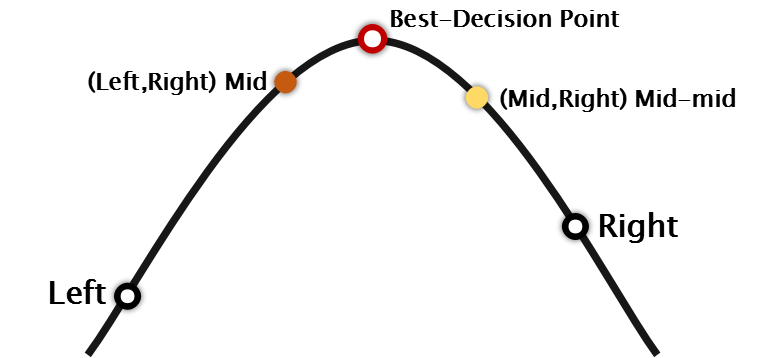
①与二分法类似,先取整个区间的中间值mid=(left+right)/2。
mid=(left+right)/2;
②再取右侧的中间值Mid-mid=(mid+right)/2。
Mid_mid=(mid+right)/2;
if(cal(mid)>cal(Mid_mid)) right=Mid_mid; else left=mid;
④重复①②③步骤,直到找到最值。
<另一种思路>
double three_devide(double low,double up) { double m1,m2; while(up-low>=eps) { m1=low+(up-low)/3; m2=up-(up-low)/3; if(f(m1)<=f(m2)) low=m1; else up=m2; } return (m1+m2)/2; }
Code
#include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #define eps 10e-6 using namespace std; const double pi=acos(double(-1)); double S; double cal(double r) { double R=S/pi/r-r; double h=sqrt(R*R-r*r); return h*pi*r*r/3; } int main() { while(~scanf("%lf",&S)) { double l=0,r=sqrt(S/pi); double m1,m2,v1,v2; while(l+eps<r) { m1=l+(r-l)/3; m2=r-(r-l)/3; v1=cal(m1); v2=cal(m2); if(v1<v2)l=m1; else r=m2; } double R=S/pi/r-r; double h=sqrt(R*R-r*r); double V=h*pi*r*r/3; printf("%.2f %.2f %.2f ",V,h,r); } return 0; }
[POJ 1987] 距离统计 (Distance Statistics)
题目描述
Farmer John现在给出一个整数K (1 <= K <= 1,000,000,000),要求你计算出相隔路程不超过K的农场的对数。
(Tips:1>被计算的农场必须是不同的两个农场;2>农场之间的路程由道路的长度决定)
输入
第1行:包含两个整数N (2 <= N <= 40,000)和M (1 <= M < 40,000)。N表示农场数,M表示道路数。
第2~M+1行:每一行给出一条道路的信息F1、F2(连接的两个农场)、L(道路长度,1 <= L <= 1000)、D(从F1到F2的方向,用N、S、W、E表示,在本题中没有作用)
第M+2行:一个整数K。
输出
符合要求的农场对数。
样例数据
| 样例输入 | 样例输出 |
7 6
1 6 13 E
6 3 9 E
3 5 7 S
4 1 3 N
2 4 20 W
4 7 2 S
10
|
5
|
<样例解释>
有5对路程不超过10的农场: 1-4 (3), 4-7 (2), 1-7 (5), 3-5 (7) 和 3-6 (9)。
解析
树的点分治"裸题"。
1、把这棵无根树以1为根节点,使其变成一棵有根树。
2、对于每棵现在要处理的树,进行如下处理:
(1)遍历这棵树,找到所有一个端点为根,路径长度不超过k的路径总数
(2)通过(1)求出的结果求和,枚举+二分计算出所有长度不超过k的的路径总数
(3)去重:也就是删去(2)中计算有重合的路径部分
(4)找到这棵子树的重心,递归处理这棵子树,也就是重复步骤2
3、统计答案并输出
[没看懂树分治?] 你还可以阅读漆子超的国家集训队论文《分治算法在树的路径问题中的应用》
Code
#include<iostream> #include<cstring> #include<cstdio> #include<algorithm>
#define MAX 40005 using namespace std; int tot=0,ans=0; int n,m,k,to[2*MAX],next[2*MAX],head[MAX],value[2*MAX]; int u[MAX],t,size[MAX],f[MAX],done[MAX]; struct wbysr { int belong,dis; }a[MAX]; bool cmp(wbysr a1,wbysr a2) { return a1.dis<a2.dis; } void add(int from,int To,int weight) { to[++tot]=To; next[tot]=head[from]; value[tot]=weight; head[from]=tot; } void dfs(int x,int fa) { u[++t]=x; size[x]=1; f[x]=0; for(int i=head[x];i;i=next[i]) if(!done[to[i]]&&to[i]!=fa) dfs(to[i],x),size[x]+=size[to[i]],f[x]=max(f[x],size[to[i]]); return; } int find_root(int x) { t=0; dfs(x,0); int Min=0x7fffffff,p; for(int i=1;i<=t;i++) if(max(size[x]-size[u[i]],f[u[i]])<=Min) Min=max(size[x]-size[u[i]],f[u[i]]),p=u[i]; return p; } void dfs2(int x,int fa,int Belong,int dist) { a[++t].belong=Belong; a[t].dis=dist; for(int i=head[x];i;i=next[i]) if(!done[to[i]]&&to[i]!=fa) dfs2(to[i],x,Belong,dist+value[i]); return; } inline void calc(int x) { t=0; a[++t].belong=x; a[t].dis=0; for(int i=head[x];i;i=next[i]) if(!done[to[i]]) dfs2(to[i],x,to[i],value[i]); sort(a+1,a+1+t,cmp); int r=t,same[MAX]={0}; for(int i=1;i<=t;i++) same[a[i].belong]++; for(int l=1;l<=t;l++) { while(a[l].dis+a[r].dis>k&&r>l) same[a[r].belong]--,r--; same[a[l].belong]--; if(r>l) ans+=r-l-same[a[l].belong]; } } inline void work(int x) { int root=find_root(x); done[root]=1; calc(root); for(int i=head[root];i;i=next[i]) if(!done[to[i]]) work(to[i]); return; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { int a1,a2,a3; char ch; scanf("%d%d%d %c",&a1,&a2,&a3,&ch); add(a1,a2,a3); add(a2,a1,a3); } scanf("%d",&k); ans=0; work(1); printf("%d ",ans); return 0; }
Time: 2017-07-15