前言
目前只会板子,板子太难背了啊
先占个坑,以后再填
Update 20210228:把坑填了
鸣谢:「笔记」Splay ----- Luckyblock 及Lb手把手的指导 我要高声赞美Lb!
Oi-wiki 及 Luckyblock 提供的图片支持
正文
简介
Splay 是一种二叉查找树,它通过不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,并且保持平衡而不至于退化为链。它由 Daniel Sleator 和 Robert Tarjan 发明。
Tarjan!又是 Tarjan!
结构
Splay 基于二叉搜索树
对于树上任意结点满足: 左儿子结点值 < 该节点值 < 右儿子结点值
结点维护信息
在接下来的叙述中,我们将遵循如下变量名习惯
root : 根节点
node_num : 已用过的节点数
now_ : 当前结点
fa[now_] : 存储 now_ 结点的父亲结点
son[now_][0/1] : 存储 now_ 结点的左/右儿子结点
val[now_] : 当前结点的值
cnt[now_] : 当前结点的出现次数
siz[now_] : 以 now_ 为根的子树大小
top : 还有几个删掉的结点
bin[] : 用来存储删掉的结点,减少结点消耗,从而减少空间
几个基本操作
Push_up(x):更新操作,更新该节点子树大小Whichson(x):判断该节点是左儿子还是右儿子clear(x):清除该节点相关信息
旋转操作
防止Splay退化成一条链造成复杂度爆炸
本质就是将某结点位置上移
大体分为左旋和右旋(其实代码一毛一样的)
粘个Oi-wiki的图
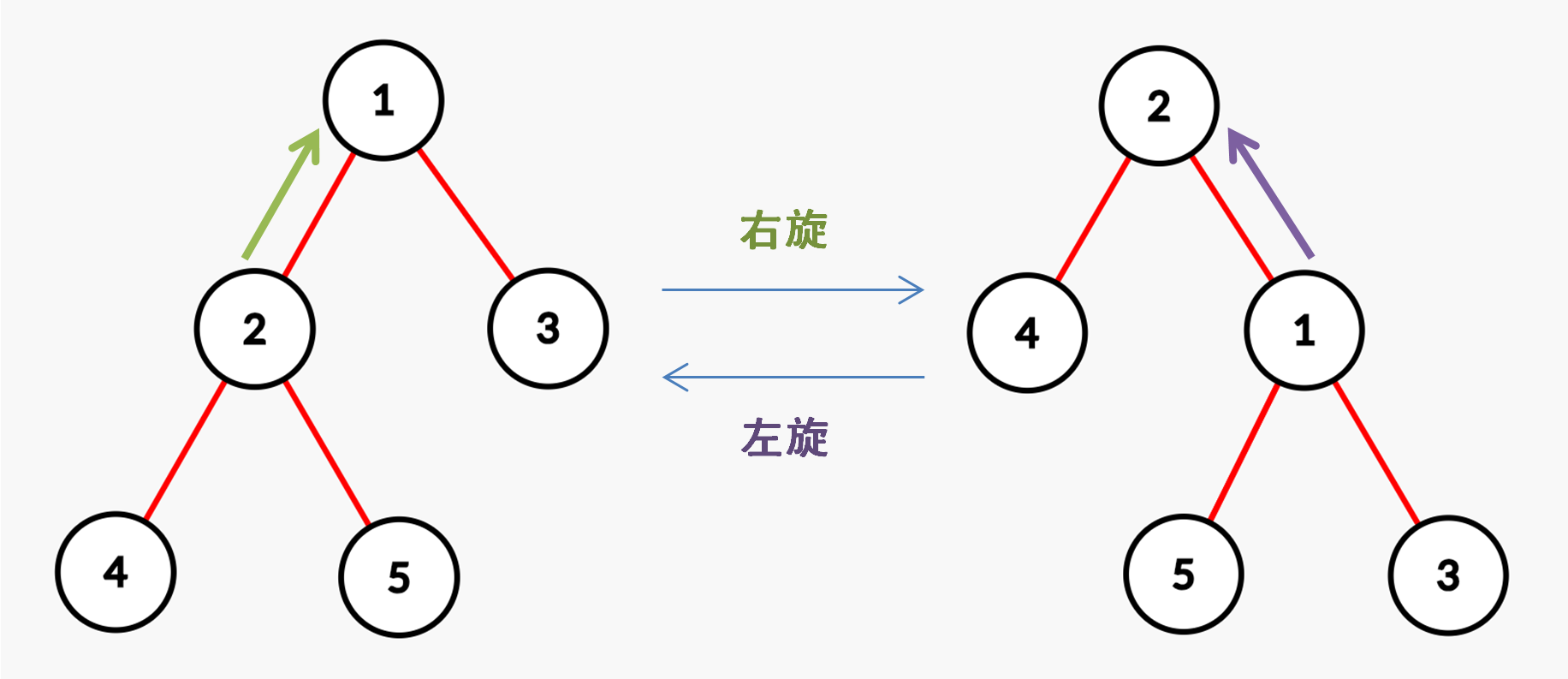
旋转时需要保证
- 树的性质不变,即仍需保证 左节点 < 该节点 < 右结点
- 结点维护的信息不变。
- root 要永远指向树根
旋转过程
观察上面的图,不难发现旋转过程分三步:
- 如果该节点有爷爷,那么让他的fa指向他的爷爷。让他替代他父亲的位置成为他爷爷的儿子。
- 如果该节点是左儿子,那么让该节点的右儿子变成该节点父亲结点的左儿子。反之让该节点的左儿子变成该节点父亲节点的右儿子。
- 如果该节点是左儿子,那么让他的父亲变成他的右儿子。反之让他的父亲变成他的左儿子。
代码实现:
void Rotate(int now_){//旋转操作
int fa_ = f, w = Whichson(now_);//查询now_是左(右)儿子
if(fa[f]) son[fa[f]][Whichson(f)] = now_;//原父亲的父亲的儿子指向now_
f = fa[f];//now_的父亲指向原父亲的父亲
son[fa_][w] = son[now_][w ^ 1];//父亲的新左儿子是now_的右儿子,父亲的新右儿子是now_的左儿子
fa[son[fa_][w]] = fa_;//原父亲的新儿子要认一个新的爸爸
son[now_][w ^ 1] = fa_;//原来的爹成为了新的儿子
fa[fa_] = now_;//原来的爹要认自己的儿子为爹
Push_up(fa_), Push_up(now_);//更新
}
Splay操作/双旋优化旋转
Splay 规定每遍历到一个结点,都要将其旋转至根节点
再借个Oi-wiki的图,其中 \(x\) 是要旋转至根节点的节点
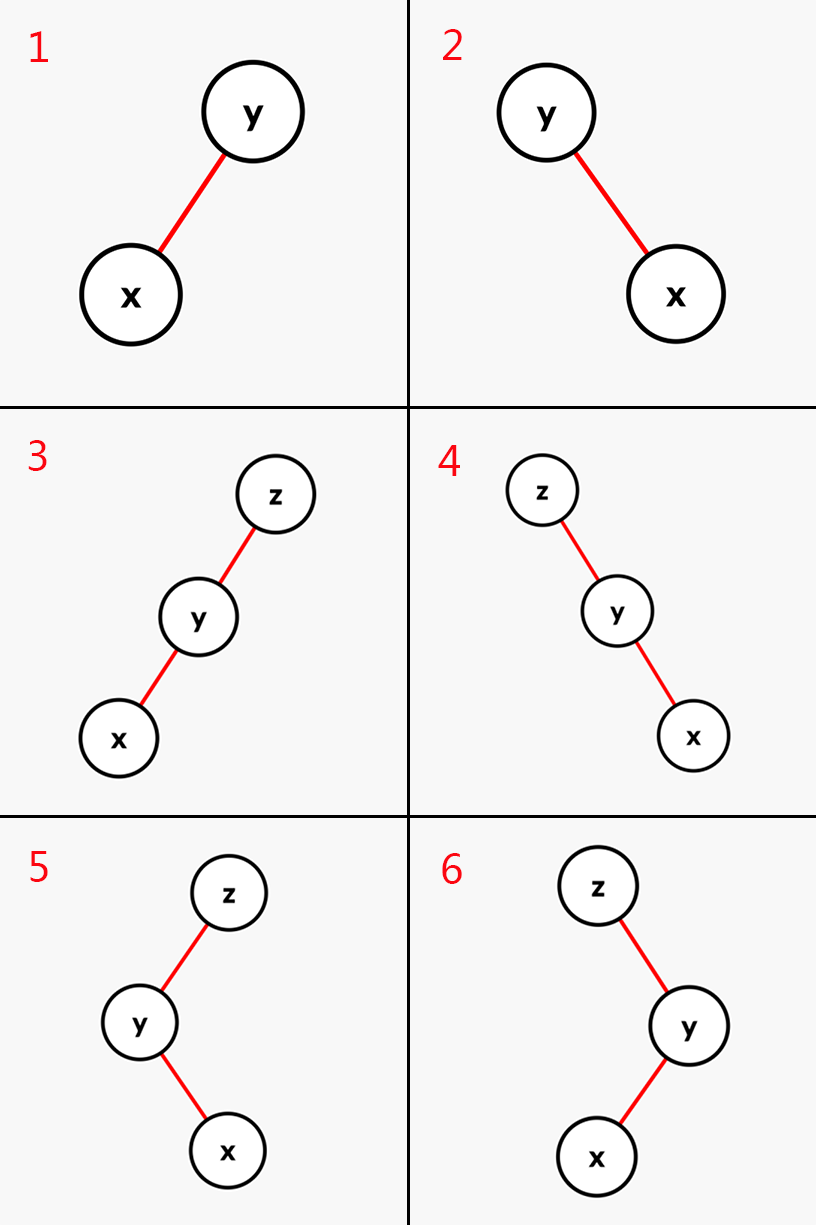
不难发现,如果在 3、4 情况下进行旋转,整棵树的深度不变
但我们知道,二叉搜索树的复杂度是与树的深度成正相关的,既然在上述情况不能降低树的深度,那么改如何做?
考虑这么一个双旋操作:
- 如果该节点和其父亲所处位置相同(都是左儿子或者都是右儿子),那么就先旋转该节点的父亲,再旋转该节点
可能看图更直观
借一下Lb的图
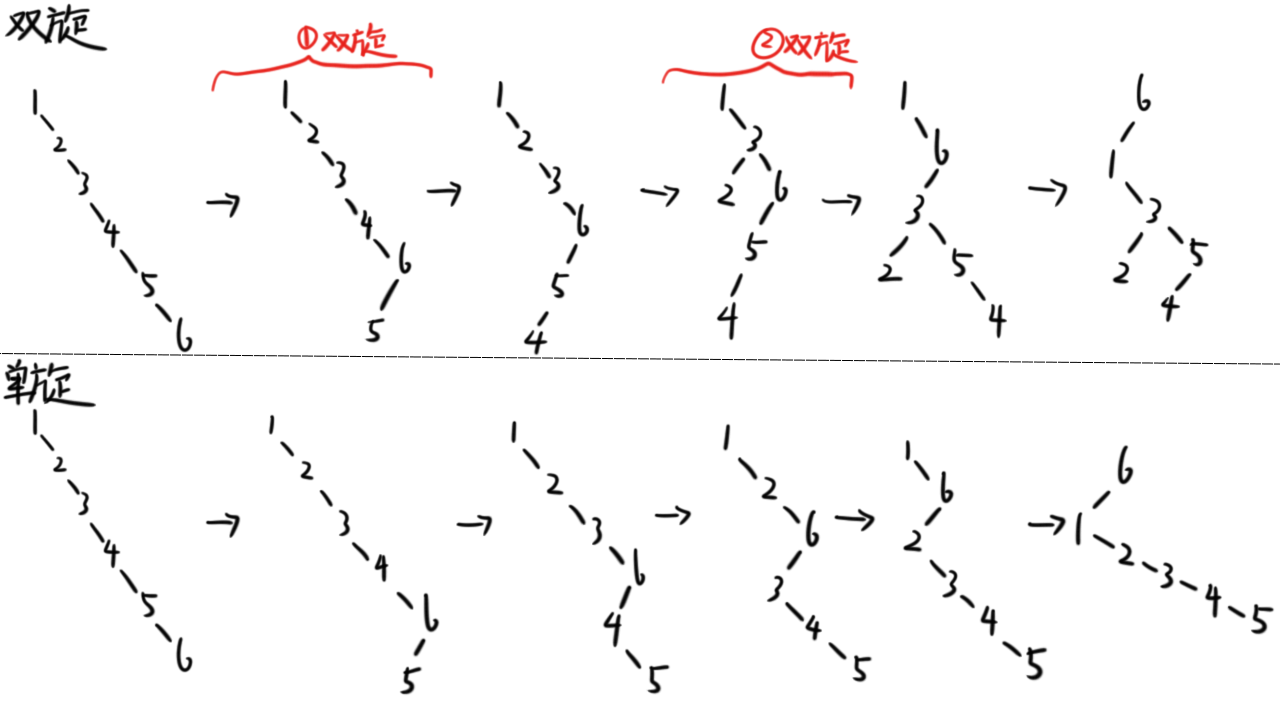
这样就可以有效减少树的深度。
也就是为什么遇到一个结点就将其旋转至根节点的原因:转的越多,树的结构就越均匀
代码实现:
void Splay(int now_){//Splay函数
for(; f; Rotate(now_)) //有父亲就再旋一次 (双旋)
if(fa[f]) Rotate(Whichson(f) == Whichson(now_) ? f : now_);//双旋操作,如果父亲还有父亲并且有相同位置的儿子,那么先旋父亲再旋儿子
root = now_;//树根更换
}
其他的几个操作
这几个操作细节较多,但都是根据 Splay 的性质来做
Insert(now_, fa_, val_):插入一个数。该点权值小于插入权值,递归到左子树;否则递归到右子树;相等就更新;没有就新建。Find(now_, val_):过程与Insert函数类似,存在返回true,不存在返回falseDelete(val_):先查询有无此数,若没有直接退出。删除时注意结点信息的清除和父子关系的改变,比较繁琐,建议直接看代码。QueryRank(val_):获取该数在树上的排名。一个简单的做法是:插入该数并将其旋转为根;查询左子树大小,答案为左子树大小+1;删除该数。正确性显然。QueryVal(rk_):查询某排名的数的值。根据左子树大小进行递归QueryPre(val_):查询某值的前驱。一个简单的做法是:插入该数并将其旋转为根;进入左子树不断想右儿子递归,不可递归时就是答案;删除该数。QueryNext(val_): 查询某个值的后继。和查询前驱类似。
板子代码
Code
代码中带有详细注释,并且进行了封装
/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
namespace Splay{
const int kMaxNode = MAXN;//
#define lson son[now_][0]
#define rson son[now_][1]
#define f fa[now_]
int node_num, root, fa[MAXN], son[MAXN][2];//分别存父亲结点 和儿子节点(0左1右)
int val[MAXN], cnt[MAXN], siz[MAXN];//分别存储权值,在当前结点的出现次数,这棵子树的大小
int top, bin[MAXN];//垃圾桶
void Push_up(int now_){//更新子树大小
siz[now_] = cnt[now_];
if(lson) siz[now_] += siz[lson];
if(rson) siz[now_] += siz[rson];
}
void Clear(int now_){//清除操作
lson = rson = f = val[now_] = cnt[now_] = siz[now_] = 0;//当前点的所有东西都变成0
bin[++top] = now_;//放进垃圾桶里
}
int NewNode(int fa_, int val_){//减少点用量?看来是
int now_ = top ? bin[top --] : ++ node_num;
f = fa_, val[now_] = val_, siz[now_] = cnt[now_] = 1;
return now_;
}
int Whichson(int now_){//查询now_是左儿子还是右儿子
return now_ == son[f][1];
}
void Rotate(int now_){//旋转操作
int fa_ = f, w = Whichson(now_);//查询now_是左(右)儿子
if(fa[f]) son[fa[f]][Whichson(f)] = now_;//原父亲的父亲的儿子指向now_
f = fa[f];//now_的父亲指向原父亲的父亲
son[fa_][w] = son[now_][w ^ 1];//父亲的新左儿子是now_的右儿子,父亲的新右儿子是now_的左儿子
fa[son[fa_][w]] = fa_;//原父亲的新儿子要认一个新的爸爸
son[now_][w ^ 1] = fa_;//原来的爹成为了新的儿子
fa[fa_] = now_;//原来的爹要认自己的儿子为爹
Push_up(fa_), Push_up(now_);//更新
}
void Splay(int now_){//Splay函数
for(; f; Rotate(now_)) {//有父亲就再旋一次 (双旋)
if(fa[f]) Rotate(Whichson(f) == Whichson(now_) ? f : now_);//双旋操作,如果父亲还有父亲并且有相同位置的儿子,那么先旋父亲再旋儿子
}
root = now_;//树根更换
}
void Insert(int now_, int fa_, int val_){//插入函数
if(now_ && val[now_] != val_) {//有根节点 并且 当前根节点不是要插的点
Insert(son[now_][val[now_] < val_], now_, val_);//如果比当前结点小就进入左儿子,否则进入右儿子
return ;
}
if(val[now_] == val_) ++ cnt[now_];//如果是这个结点,cnt++
if(!now_) {//如果没有点了,开一个新点
now_ = NewNode(fa_, val_);//获取新点的点号
if(f) son[f][val[f] < val_] = now_;//如果新点比父亲结点小就放左边,否则放右边
}
Push_up(now_), Push_up(f), Splay(now_);
}
int Find(int now_, int val_){//查询函数
if(!now_) return false;//如果没有该节点,返回0
if(val_ < val[now_]) return Find(lson, val_);//如果比当前结点小。查询左子树
if(val_ == val[now_]) {//如果是这个结点, 顺便把这个点旋转到树的顶端(这样更新结点大小时只需要考虑根节点了
Splay(now_);
return true;
}
return Find(rson, val_);//查询右子树
}
void Delete(int val_){//删除操作
if(!Find(root, val_)) return ;//如果没找到这个点,直接返回
if(cnt[root] > 1){//如果当前结点出现次数超过1,直接减掉
-- cnt[root];
Push_up(root);//更新一下
return ;
}
int oldroot = root;//记录旧的树根
if(!son[root][0] && !son[root][1]){//如果左右儿子都没有
root = 0;//把树根改为0
}
else if(!son[root][0]){//如果没有左儿子
root = son[root][1], fa[root] = 0;//让右儿子成为父亲,根节点没有父亲
}
else if(!son[root][1]){//如果没有右儿子
root = son[root][0], fa[root] = 0;//让左儿子成为父亲,根节点没有父亲
}
else if(son[root][1] && son[root][0]) {//如果两个儿子都有
int leftmax = son[root][0];//钦定选原根节点的前驱
while(son[leftmax][1]) leftmax = son[leftmax][1];//找前驱
Splay(leftmax);//将前驱提到跟结点上
son[root][1] = son[oldroot][1], fa[son[root][1]] = root;//更新新节点的右儿子,原右儿子的父亲
}
Clear(oldroot), Push_up(root);//清理原树根,更新新树根
}
int QueryRank(int val_){//获取排名 (还可以用一种递归的方式去写,可能码量比较多?
Insert(root, 0, val_);//插入这个数
int ret = siz[son[root][0]] + 1;//排名就是左子树加1
Delete(val_);//删掉这个数
return ret;
}
int QueryVal(int rk_){//查询第rk_名的值
int now_ = root;//获取树根
while(true) {
if(!now_) return -1;//若没有树根,表示没有任何树,返回-1
if(lson && siz[lson] >= rk_){//注意 = 此时一定在左子树内
now_ = lson;// 进入左子树
} else{
rk_ -= lson ? siz[lson] : 0; //减掉左子树中的点 (不含根
if( rk_ <= cnt[now_]) {//如果当前排名在根节点中
Splay(now_);//将根节点转到树根
return val[now_];//返回根节点的值
}
rk_ -= cnt[now_];//减掉根节点中的排名
now_ = rson;//进入右子树
}
}
}
int QueryPre(int val_){//获取前驱
Insert(root, 0, val_);//插入这个点
int now_ = son[root][0];//答案一定在左子树中
while(rson) now_ = rson;//找前驱
Delete(val_);//删掉刚刚插入的点
return val[now_];//返回当前点的值
}
int QueryNext(int val_){//获取后继
Insert(root, 0, val_);//插入这个点
int now_ = son[root][1];//答案一定在柚子树中
while(lson) now_ = lson;//找后继
Delete(val_); //删掉刚刚插入的点
return val[now_];//返回当前点的值
}
}
int main()
{
int n = read();
while(n--){
int opt = read(), x = read();
if(opt == 1) {//插入x数
Splay::Insert(Splay::root, 0, x);
} else if(opt == 2){//删除x数
Splay::Delete(x);
} else if(opt == 3){//获取排名
printf("%d\n", Splay::QueryRank(x));
} else if(opt == 4){//查询第x名是哪个数
printf("%d\n", Splay::QueryVal(x));
} else if(opt == 5){//求x的前驱
printf("%d\n", Splay::QueryPre(x));
} else if(opt == 6){//求x的后驱
printf("%d\n", Splay::QueryNext(x));
}
}
return 0;
}