笛卡尔树+树形dp
你会发现,如果有两个高度分别为(h[i])和(h[j])(满足(i<j))的棋盘,存在一个k满足(i<k<j)且(h[i]>h[k],h[j]>h[k]),那么在任意高度H满足(H>min{h[k]}k in [i+1,j-1])的i和j棋盘都不会相互制约的。
那么,我们能不能先在n个棋盘中找到一个最小的h,那么其两旁的棋盘在大于h的地方摆放都是不会互相影响的,那我们只用先算出在两旁大于h的地方摆放棋子的方案数,再合并一下,最后再统一算一遍这n个棋盘都在小于等于h的地方摆放的方案数,再累到答案中去。
而对于统计其两旁棋盘的方案数,我们可以按照上述方法递归下去。
于是,这就需要用到笛卡尔树了。
笛卡尔树是一种特定的二叉树数据结构,可由数列构造,在范围最值查询、范围top k查询(range top k queries)等问题上有广泛应用。它具有堆的有序性,中序遍历可以输出原数列。笛卡尔树结构由Vuillmin(1980)在解决范围搜索的几何数据结构问题时提出。从数列中构造一棵笛卡尔树可以线性时间完成,需要采用基于栈的算法来找到在该数列中的所有最近小数。
摘自度娘
说白了,笛卡尔树就是这样一个东西:
1.二叉树
2.若只看权值,则其每个点在权值上形成一个堆
3.若只看下标,则其每个点在下标上形成一个二叉搜索树
它就是长这个样子。
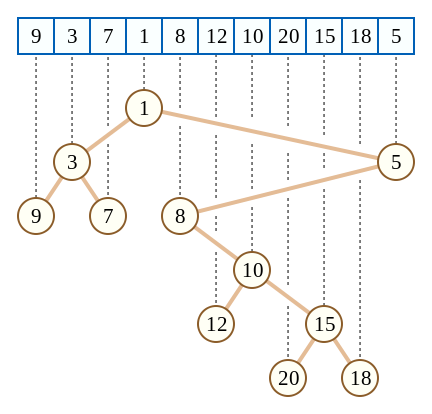
建树的话,上面已经提到,它可以在(O(n))时间内利用单调栈完成,大致流程如下:(假定我们构建的是小根堆)
对于新加进一个数x,设栈顶元素为top
1.如果(x>top),则将top的右儿子设置为x
2.如果(x le top),则将top弹出,当(top>x)或者栈为空为止,记最后一个弹出的数为la,则将la设置为x的左二子;若栈不为空,则将x设置为top的右儿子
代码如下:
for(int i=1; i<=n; i++) {
int res=-1;
while(head<=tail&&A[i]<=A[Q[tail]])res=Q[tail--];
if(res!=-1) {
if(rt==res)rt=i;
ch[i][0]=res;
}
if(head<=tail)ch[Q[tail]][1]=i;
Q[++tail]=i;
}
不太懂得人建议先去做一下HDU1506。
回到这道题,我们构建一棵笛卡尔树后,就可以在上面跑树形dp了。
(dp[x][i])表示在以x为根的子树中,放了i个棋子且放的位置大于(h[fa])的方案数,其中fa表示x的父亲
那么,转移就直接拿左右儿子合并就好了:
dp[x][0]=1;
size[x]=1;
for(int i=0; i<=1; i++) {
int t=ch[x][i];
if(t==0)continue;
DFS(t,x);
for(int i=min(K,size[x]); i>=0; i--) {
for(int j=min(K,size[t]); j>=1; j--) {
if(i+j>K)continue;
if(i+j==0)continue;
dp[x][i+j]=(dp[x][i+j]+dp[x][i]*dp[t][j]%MOD)%MOD;
}
}
size[x]+=size[t];
}
那么,现在我们就要考虑在([h[fa]+1,h[x]])这一区间放棋子的方案数了。
由于以x为根的子树在序列中对应的都是连续区间,那么它们彼此之间必定互相牵制。
于是问题就转化成了:
给定一个(size[x]*(h[x]-h[fa]))的矩阵,在其中放K个棋子,其中每行每列最多只能放一个的方案数(假设(size[x])和(h[x]-h[fa])都大于K)。
那么显然,我们现在(size[x])中选K行,再在(h[x]-h[fa])中选K列,那么一共有(C_{size[x]}^{K}cdot C_{h[x]-h[fa]}^{K})种方案,对于每种方案,棋子又有(K!)种排法,于是一共有(C_{size[x]}^{K}cdot C_{h[x]-h[fa]}^{K} cdot K!)种方案。
那么,我们在合并后枚举K,然后再转移一波。
于是,这道题就愉快的A了。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD=1000000007;
int n,K,rt,head,tail,A[1010],ch[1010][2],Q[1010],dp[1010][1010],size[1010],frac[1001000],inv[1001000],infr[1001000];
int Quick_Pow(int a,int p){
int res=1;
while(p){
if(p&1)res=res*a%MOD;
a=a*a%MOD;
p>>=1;
}
return res;
}
int C(int x,int y){
if(x<y)return 0;
return frac[x]*infr[y]%MOD*infr[x-y]%MOD;
}
void DFS(int x,int fa){
dp[x][0]=1;
size[x]=1;
for(int i=0;i<=1;i++){
int t=ch[x][i];
if(t==0)continue;
DFS(t,x);
for(int i=min(K,size[x]);i>=0;i--){
for(int j=min(K,size[t]);j>=1;j--){
if(i+j>K)continue;
if(i+j==0)continue;
dp[x][i+j]=(dp[x][i+j]+dp[x][i]*dp[t][j]%MOD)%MOD;
}
}
size[x]+=size[t];
}
int cha=A[x]-A[fa];
for(int i=min(size[x],K);i>=0;i--){
for(int j=size[x]-i;j>=1;j--){
if(i+j>K)continue;
if(i+j==0)continue;
dp[x][i+j]=(dp[x][i+j]+dp[x][i]*C(size[x]-i,j)%MOD*C(cha,j)%MOD*frac[j]%MOD)%MOD;
}
}
}
void init(){
frac[0]=infr[0]=1;
for(int i=1;i<=1000010;i++)inv[i]=Quick_Pow(i,MOD-2);
for(int i=1;i<=1000010;i++)frac[i]=frac[i-1]*i%MOD,infr[i]=infr[i-1]*inv[i]%MOD;
}
signed main() {
init();
scanf("%lld %lld",&n,&K);
rt=1,head=1,tail=0;
for(int i=1; i<=n; i++)scanf("%lld",&A[i]);
for(int i=1; i<=n; i++) {
int res=-1;
while(head<=tail&&A[i]<=A[Q[tail]])res=Q[tail--];
if(res!=-1) {
if(rt==res)rt=i;
ch[i][0]=res;
}
if(head<=tail)ch[Q[tail]][1]=i;
Q[++tail]=i;
}
DFS(rt,0);
printf("%lld",dp[rt][K]);
return 0;
}