学习笔记-2022.03.01
内容:阅读论文分享:HyperDQN: A Randomized Exploration for Deep RL
Introduction
-
强化学习的一个难题是与环境交互时的样本效率
- 好的探索策略可以减小样本复杂度。一个好的探索策略要不断尝试那些未知的/不确定的动作;但是对于已经比较确信的动作,应该采取最优的动作。
- 差的探索策略则可能导致即使交互了很多次,也无法求解到最优策略。
-
目前比较认可的高效探索策略
-
Upper Confidence Bound (UCB)
置信区间上届算法,乐观的算法。。。
UCB方法会设计“exploration bonus”来确保Q-value function是乐观的,这样便不会遗漏掉选择最优动作的可能。
-
Thompson Sampling (TS)
汤普森采样
Thompon Sampling的方法会通过后验分布来刻画不确定度:如果后验分布比较“宽”,则认为对环境的不确定比较大,如果后验分布比较“窄”,则认为对环境的不确定度比较小。除此之外,通过从后验分布中采样,Thompson Sampling的方法也可以实现像UCB那样的乐观估计。

上图引自知乎
-
大量研究表示Thompson Sampling的方法实际性能会比UCB更好一些。
-
-
但想要把Thompson Sampling的方法应用在RL里并不那么容易
一个主要的难题是如果更新后验分布。后验分布取决于先验分布和似然函数。如果我们考虑线性模型,那么后验分布更新还是可行的。这种情况下的算法就是著名的Randomized Least-square Value Iteration (RLSVI)。但是RLSVI和Deep RL并不兼容:
- RLSVI里假设线性模型有一个比较好的特征(feature),从而可以表达最优的Q-value function。但这这个假设在实际任务中很难满足,因为我们实现不知道一个好的特征是什么,而需要神经网络来不断学习。
- 当特征在不断变化的时候,RLSVI里的更新公式便不再适用,这意味着后验分布很难求解。
-
论文主要工作是解决了以上问题。
Methodology
-
方法里有两个模型: base model和hypermodel:
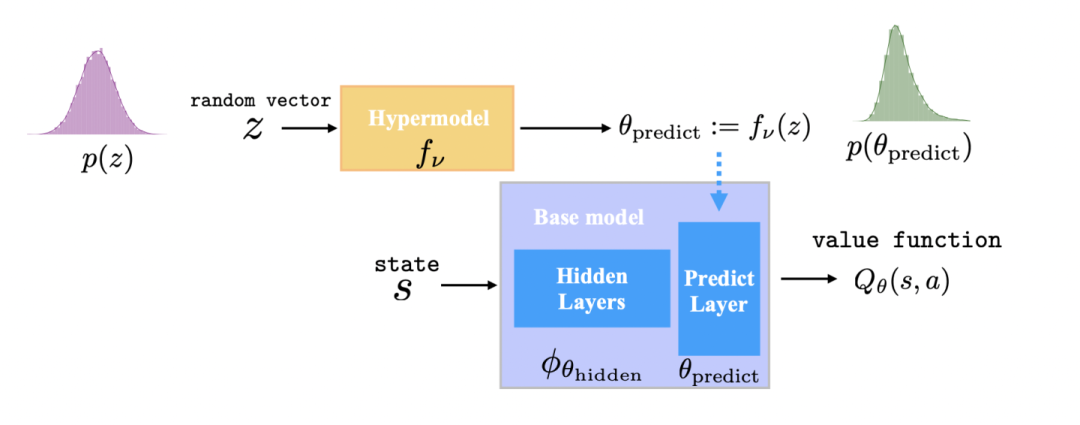
-
base model就是一个基本的DQN模型(base model的参数是从hypermodel里采样得到的)。
-
hypermodel则是一个meta model来度量base model的parameter uncertainty
在Thompson Sampling方法里,我们把对环境的不确定度转化为对模型参数的不确定度。
-
-
为了把base model (feature extractor)和hypermodel (posterior distribution)学习出来,研究者设计了目标函数:
\[\min_{v,\theta_{hidden}} \int_z {p(z)[\sum_{(s,a,r,\xi,s')∈D} (Q_{target} (s',z) + \delta_{\omega} z^{\top} \xi - Q_{prediction} (s,a,z)^2 + \frac{\delta_{\omega}^2}{\delta_{p}^2} ||f_v (z)||^2) ](dz)} \tag{1} \]其中,
\[Q_{prediction} (s,a,z) = Q_{\theta_{prior, f_{v_{prior}}(z)}} (s,a) + Q_{\theta_{hidden, f_{v}(z)}}(s,a) \tag{2} \]\[Q_{target} (s',z) = r + \gamma \max_{a'} [Q_{\theta_{prior, f_{v_{prior}}(z)}}(s',a') + Q_{\overline{\theta}_{hidden, f_{v}(z)}}(s',a')] \tag{3} \]此处为一个高斯分布, \(z \top \xi\) 是一个认为引入的噪声
Experiment
实验结果参考原文,结果就是性能比DQN好,在大部分游戏中的表现好于baselines,计算代价比BootDQN小。