之前参加阿里巴巴的笔试碰到一最大网络流的题目。因为之前没有看过这类算法,所以还是自然没做出。今天抽空看了看。了解了下基本概念和求解流程。这里简单总结下。
主要内容来自百度文库某ppt。在每幅图片的下面我会给出一些说明性文字。
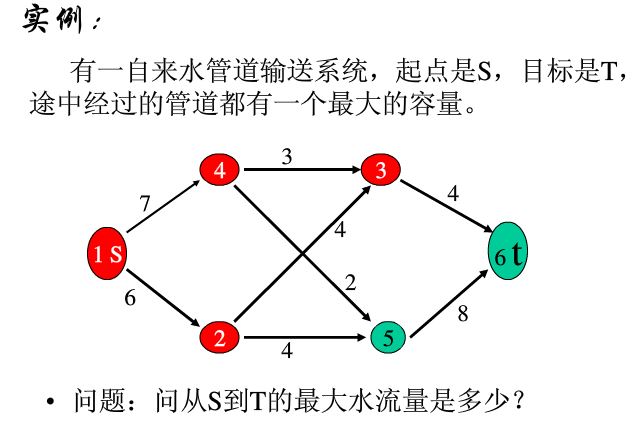
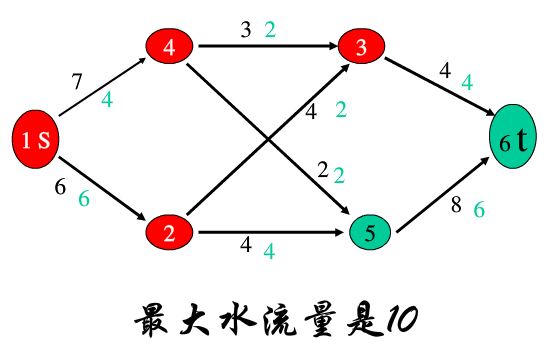
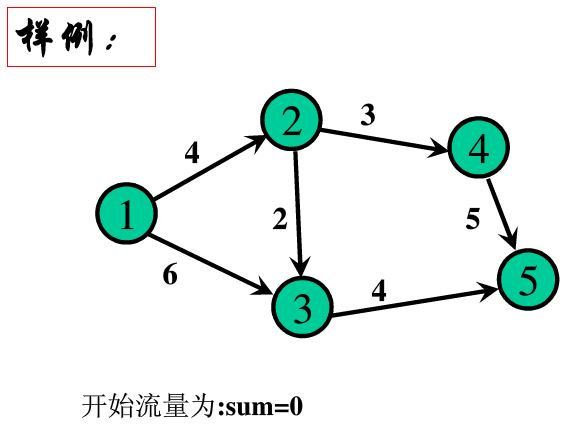
本图示最大流的一个实例。由此,可以引出最大流的一些基本的定义和概念

可以这样看,图就是一种管道,管道有最大通过流量的限制,图中边的权值就是所谓的“容量”。同时,注意有唯一的源点和汇点。

这里需要注意容量和流量的区别。其中f(u,v)的范围需要额外注意,是 0<= f(u,v) <= c(u,v),不会出现所谓的负流量。下图是对可行流的图示

有了可行流,我们还需要求最大流

那么如何求最大流呢。可以采用著名的Ford Fulkerson算法

所以说,算法的关键在于
1)何为增广路径,如何找出增广路径。
2)如何更新流量
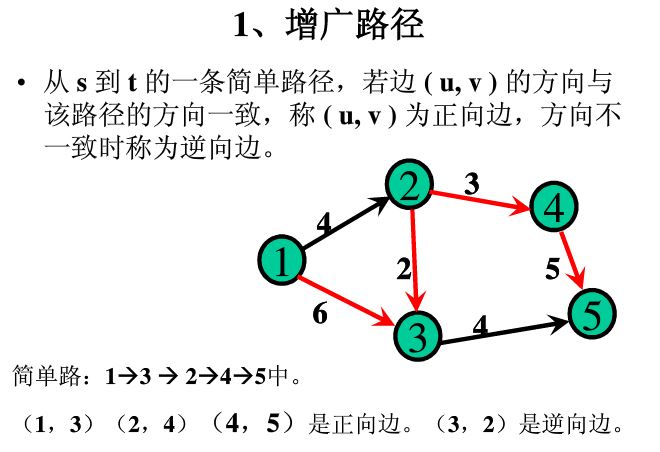
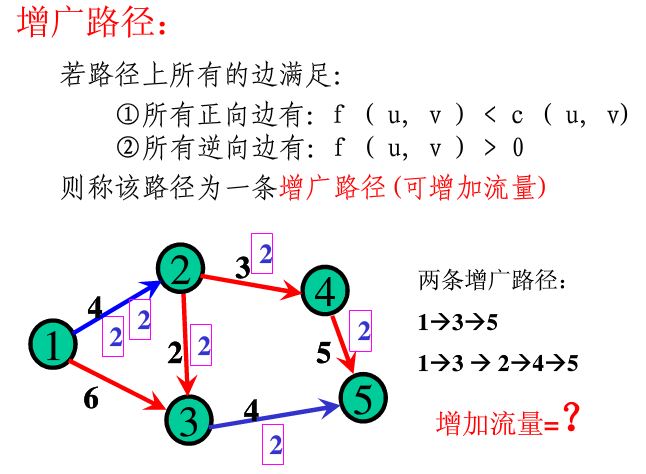
说的直白些,所谓增广路径,就是找到这样一条路径,其流量不满,未达到容量上限。
所有的可能的增广路径在一起便构成了残留网络。
那么,如何增广呢。

其实,这里的这个描述不太准确。下面我根据我的理解再解释一下。
第一步,计算可增加流量
设某一增广路径上的节点为(a1,a2,a3,a4,....,an)
如果(u,v)是正向边,则增加流量d = min{ c(ai,aj) - f(ai,aj) | j = i +1, i =1,2,3...,n-1}
如果是逆向边,则增加流量d = min{ f(ai, aj) | j = i +1, i =1,2,3...,n-1}
第二步,更新流量
如果(u,v)是正向边,则 f(u,v) = f(u,v) + d
是逆向边,则f(u,v) = f(u,v) - d
注意,如果是逆向边,就是减法,当前管道从中减去部分流量,而且,伴随着这部分减去的流量,必有另一部分管道的流量会增加。。而且,最后的总流量增加了d
结合上述算法,可以详细参阅下下列图示

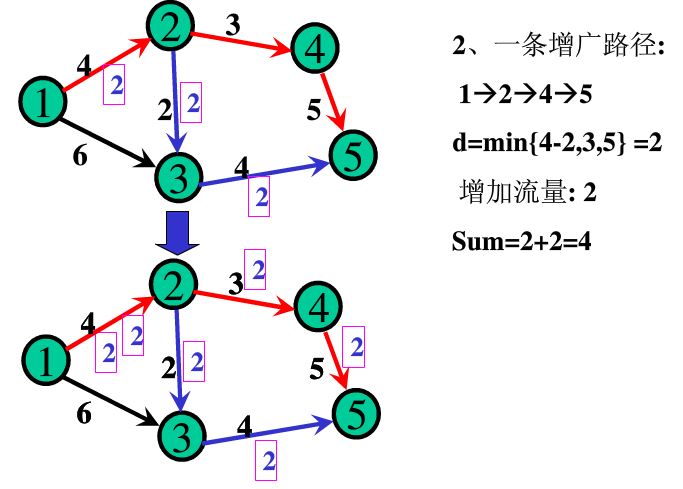

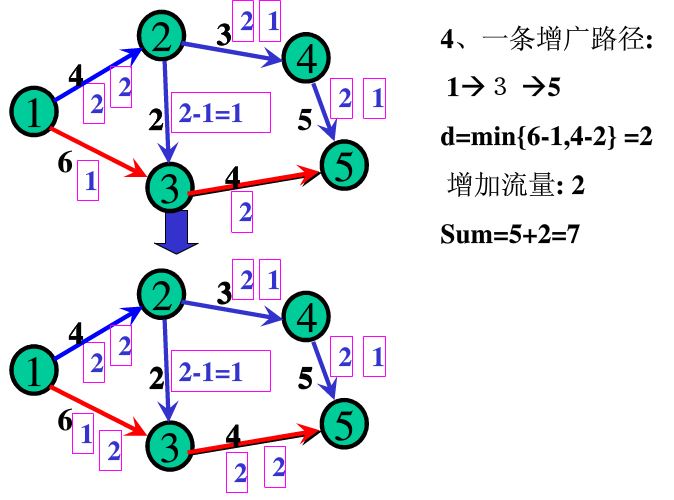
可以证明,可行流为最大流,当且仅当不存在新的增广路径。
总结一下最大流算法

如何寻找增广路径,采用DFS和BFS的方法。然后在更新流量。
具体实现以后再给出。
源PPT链接http://wenku.baidu.com/view/7ed3c241a8956bec0975e32b.html