一、插入排序的介绍
插入排序的工作方式非常像人们排序一手扑克牌一样。开始时,我们的左手为空并且桌子上的牌面朝下。然后,我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置,我们从右到左将它与已在手中的每张牌进行比较,如下图所示:

那插曲排序是如何借助上面提到的思想来实现排序的呢?首先我们将数组中的数据分为两个区间,已排序区间和未排序区间。初始已排序区间只有一个元素,就是数组的第一个元素,然后在未排序区间中依次取出元素并插入到已排序区间的合适位置,并保证已排序区间一直是有序。重复这个步骤直到未排序区间元素为空,算法结束。
插入排序算法是基于某序列已经有序排列的情况下,通过一次插入一个元素的方式按照原有排序方式增加元素。这种比较是从该有序序列的最末端开始执行,即要插入序列中的元素最先和有序序列中最大的元素比较,若其大于该最大元素,则可直接插入最大元素的后面即可,否则再向前一位比较查找直至找到应该插入的位置为止。插入排序的基本思想是,每次将1个待排序的记录按其关键字大小插入到前面已经排好序的子序列中,寻找最适当的位置,直至全部记录插入完毕。执行过程中,若遇到和插入元素相等的位置,则将要插人的元素放在该相等元素的后面,因此插入该元素后并未改变原序列的前后顺序。我们认为插入排序也是一种稳定的排序方法。插入排序分直接插入排序、折半插入排序和希尔排序3类。
二、插入排序的原理
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
三、插入排序的图解
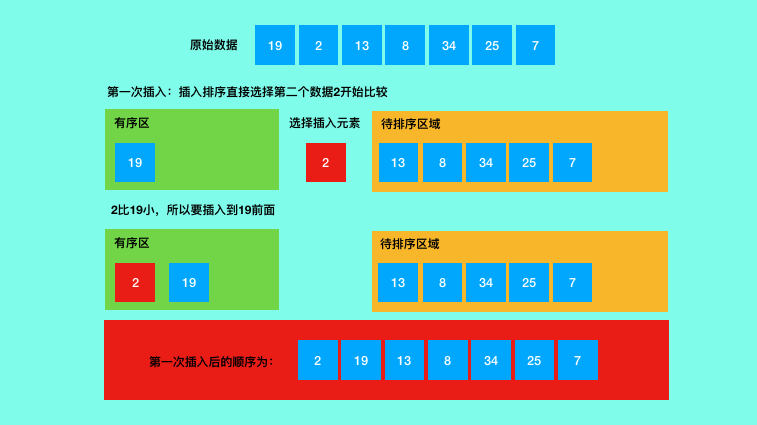

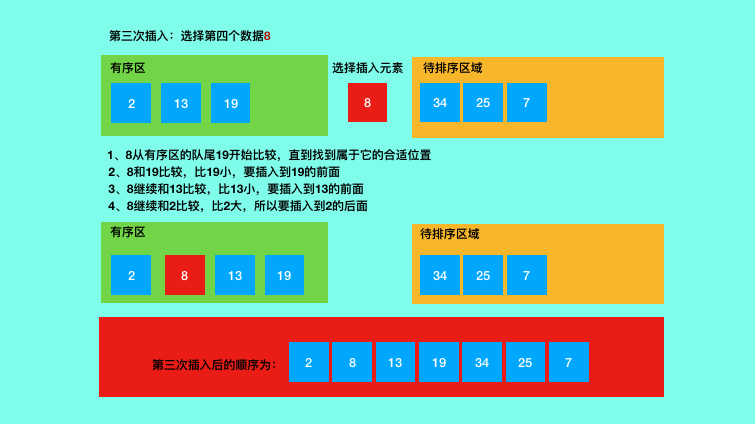

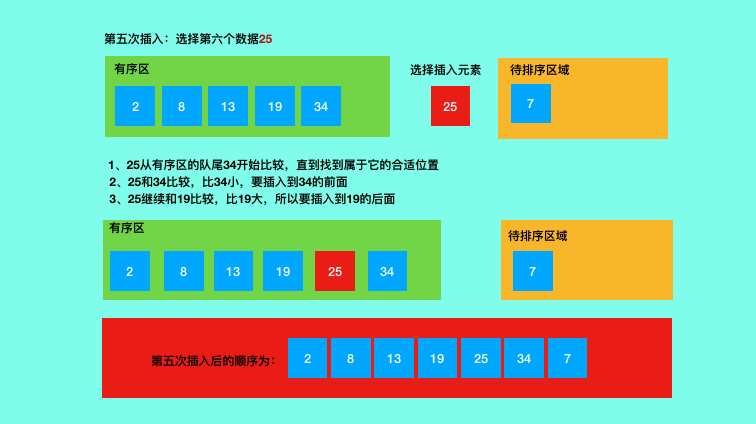
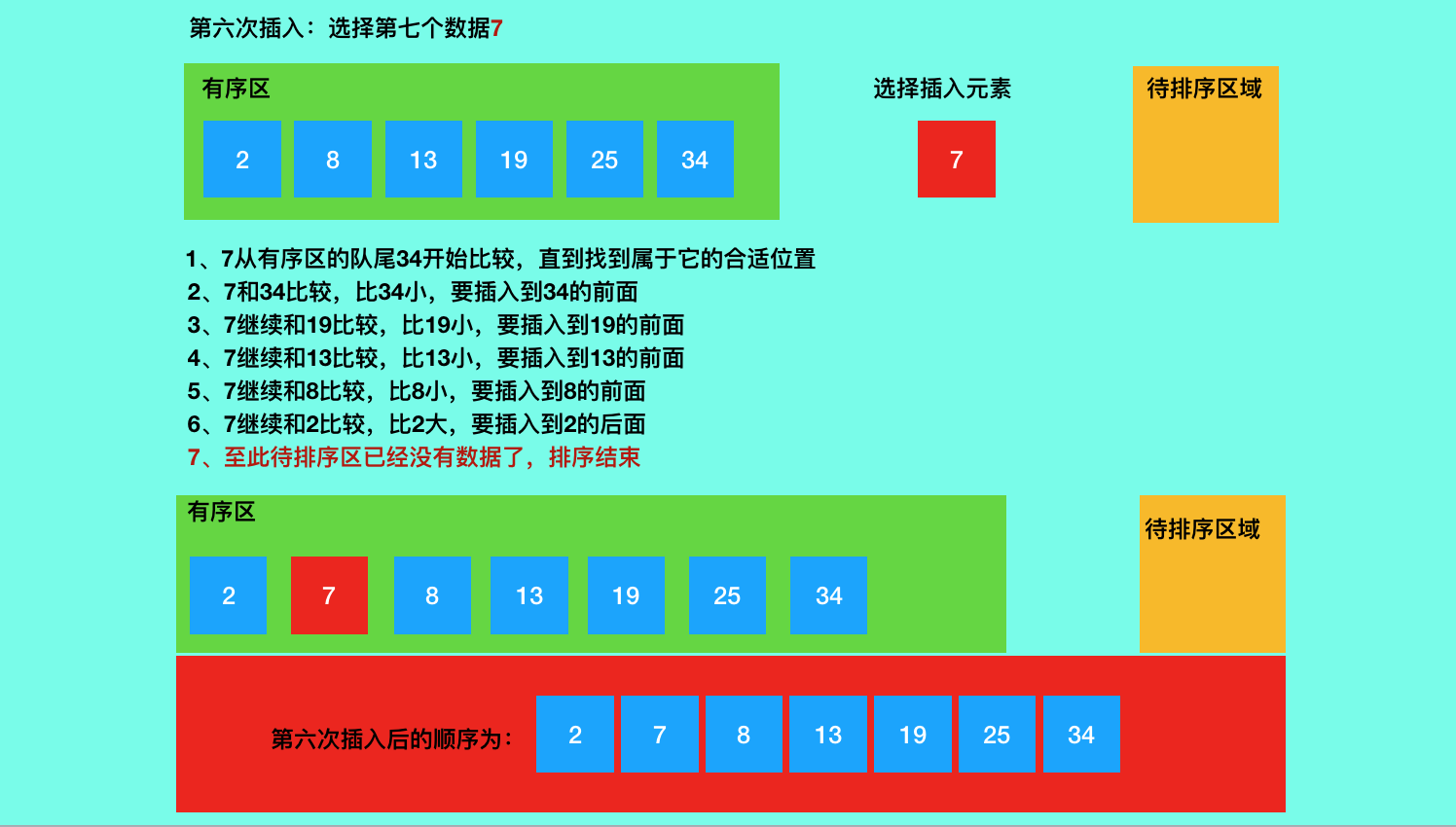
四、插入排序的python代码实现
# 定义插入排序函数 def insertion_sort(list): # 获取需要排序数据的个数 N = len(list) # 插入排序的第一次插入从第二个数字开始选择,所以下标从1开始 for i in range(1,N): # 从选择插入的数据,一次和它前一个比较,主要比前面的小就交换 for j in range(i,0,-1): # 判断大小 if list[j]<list[j-1]: # 交换 temp = list[j] list[j] = list[j-1] list[j-1] = temp numlist = [19,2,13,8,34,25,7] print("排序前:%s"%numlist) insertion_sort(numlist) print("排序后:%s"%numlist)
运行结果为:
排序前:[19, 2, 13, 8, 34, 25, 7]
排序后:[2, 7, 8, 13, 19, 25, 34]
五、插入排序的C语言代码实现
#include <stdio.h> // 定义插入排序函数 void insertion_sort(int array[],int ArrayLenght) { // 插入排序的第一次插入从第二个数字开始选择,所以下标从1开始 for (int i=1; i<ArrayLenght; i++) { // 从选择插入的数据,一次和它前一个比较,主要比前面的小就交换 for (int j=i; j>0; j--) { // 判断大小 if (array[j]<array[j-1]) { // 交换 int temp = array[j]; array[j] = array[j-1]; array[j-1] = temp; } } } } int main(int argc, const char * argv[]) { // 插入排序函数的声明 void insertion_sort(int array[],int ArrayLenght); // 需要排序的数组 int a[] = {19,2,13,8,34,25,7}; // 调用插入排序 insertion_sort(a, 7); // 打印验证 for (int i =0; i<7; i++) { printf("%d ",a[i]); } return 0; }
运行结果为:
2 7 8 13 19 25 34
六、插入排序的时间复杂度
- 最优时间复杂度:O(n) (升序排列,序列已经处于升序状态)
- 最坏时间复杂度:O(n^2)
七、插入排序的稳定性
插入排序的基本思想是,每次将1个待排序的数据按其大小插入到前面已经排好序的子序列中,寻找最适当的位置,直至全部记录插入完毕。执行过程中,若遇到和插入元素相等的位置,则将要插人的元素放在该相等元素的后面,因此插入该元素后并未改变原序列的前后顺序。我们认为插入排序也是一种稳定的排序方法。