一、选择排序的介绍
选择排序(Selection sort)是一种简单直观的排序算法。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。选择排序每次交换一对元素,它们当中至少有一个将被移到其最终位置上,因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种。
二、选择排序的原理
- 在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
- 再从剩余未排序元素中继续寻找最小(大)元素
- 然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
三、选择排序的图解
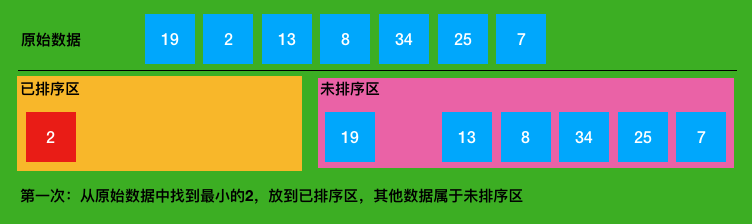





四、选择排序总结
- 有N个数据,需要从未排序区挑选N-1次数据放在已排序区队尾
- 每次从未排序区中挑选的数据要放在已排序的队尾
五、选择排序的python代码实现
# 定义选择排序函数 def selection_sort(list): # 计算需要排序的列表元素个数 N = len(list) # 需要N-1次选择操作 for i in range(N-1): # 记录最小值的小标 minNum_index = i # 未排序区域从i+1到末尾N处,属于未排序区,在未排序区在选出最小值处 for j in range(i+1,N): # 比较大小 if list[minNum_index]>list[j]: #交换 temp = list[minNum_index] list[minNum_index] = list[j] list[j] = temp # 创建一个列表 numList = [19,2,13,8,34,25,7] print("排序前:%s"%numList) # 调用选择排序 selection_sort(numList) print("排序后:%s"%numList)
运行结果为:
排序前:[19, 2, 13, 8, 34, 25, 7]
排序后:[2, 7, 8, 13, 19, 25, 34]
六、选择排序的C语言代码实现
版本一
#include <stdio.h> //定义选择排序函数 void selection_sort(int array[],int arrayLenght) { // 需要N-1次选择操作 for (int i=0; i<arrayLenght-1; i++) { // 记录最小值的下标 int minNum_index = i; // 未排序区域从i+1到末尾N处,属于未排序区,在未排序区再选出最小值处 for (int j = i+1; j<arrayLenght; j++) { // 比较大小 if (array[minNum_index]>array[j]) { // 交换 int temp = array[minNum_index]; array[minNum_index] = array[j]; array[j] = temp; } } } } int main(int argc, const char * argv[]) { // 选择排序函数声明 void selection_sort(int array[],int arrayLenght); // 创建数组 int numArray[] = {19,2,13,8,34,25,7}; // 调用排序 selection_sort(numArray, 7); // 验证 for (int i =0; i<7; i++) { printf("%d ",numArray[i]); } return 0; }
运行结果为:
2 7 8 13 19 25 34
版本二
#include <stdio.h> //定义选择排序函数 void selection_sort1(int array[],int arrayLenght) { // 需要N-1次选择操作 for (int i=0; i<arrayLenght-1; i++) { // 记录最小值的下标 int minNum_index = i; // 未排序区域从i+1到末尾N处,属于未排序区,在未排序区再选出最小值处 for (int j = i+1; j<arrayLenght; j++) { // 比较大小 if (array[minNum_index]>array[j]) { minNum_index = j; } } if (minNum_index != i) { int temp = array[i]; array[i] = array[minNum_index]; array[minNum_index] = temp; } } } int main(int argc, const char * argv[]) { // 选择排序函数声明 void selection_sort1(int array[],int arrayLenght); // 创建数组 int numArray[] = {19,2,13,8,34,25,7}; // 调用排序 selection_sort1(numArray, 7); // 验证 for (int i =0; i<7; i++) { printf("%d ",numArray[i]); } return 0; }
运行结果为:
2 7 8 13 19 25 34
七、选择排序的时间复杂度
- 最优时间复杂度:O(n2)
- 最坏时间复杂度:O(n2)
八、选择排序的稳定性
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推,直到第n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,如果一个元素比当前元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。比较拗口,举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中两个5的相对前后顺序就被破坏了,所以选择排序是一个不稳定的排序算法。