多边形序列（组合数）（高精）（NTT）

多边形序列

题目大意

一个由 LR 组成的序列，可以构造一个多边形，L 表示 90 度的角，R 表示 270 度的。
然后一个可视的多边形是你可以在多边形内部找到一个点可以看到多边形的每个点。
给你序列长度，问你有多少种序列满足可以构成的直角多边形中有可视的。

思路

你看一下图，你会发现一个东西，就是它不可能出现凸字形的。

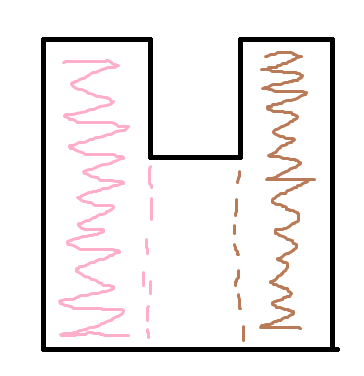
你看这个图形，它如果要左边凸出来被看到，就一定要在粉色的区域，如果有右边凸出来被看到，就一定要在棕色的区域，你无论在哪个位置，都会有一个凸出来的看不到。

那你搞一搞会发现它其实就是一堆 LR（RL），然后里面有四个 L 来转方向。
然后不难看到不能有两个 R 在一起，因为就会出现凹字形。

那就是 (dfrac{n-4}{2}) 个 R，(dfrac{n+4}{2}) 个 L，R 不能放在一起。

不难想到插空法得到组合数，但是你还要去一种不合法的。
因为你是环形，你是不可以在最两边都放 R 的。

所以你要一种是一定要一边，一种是一个都不要。
然后就是 (C_{x}^4+C_{x-1}^4)。

然后就要用高精，乘法就要用 FFT 或者 NTT，我这里用的是 NTT。

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
#define mo 998244353
#define G 3

using namespace std;

struct gj {
	int n;
	ll a[800001];
}n, x, x1, x2, x3;
char s[100001];
int sn, limit, ln, an[800001];
ll Gv;

ll ksm(ll x, ll y) {
	ll re = 1;
	while (y) {
		if (y & 1) re = (re * x) % mo;
		x = (x * x) % mo;
		y >>= 1;
	}
	return re;
}

void chu(gj &now, int x) {
	for (int i = now.n; i >= 0; i--) {
		if (i) now.a[i - 1] += 10 * (now.a[i] % x);
		now.a[i] = now.a[i] / x;
	}
	while (!now.a[now.n]) now.n--;
}

void jian(gj &now, int x) {
	now.a[0] -= x;
	int tmp = 0;
	while (now.a[tmp] < 0) {
		now.a[tmp + 1] -= -1 * now.a[tmp] / 10;
		now.a[tmp] += -1 * now.a[tmp] / 10 * 10;
		if (now.a[tmp] < 0) now.a[tmp + 1]--, now.a[tmp] += 10;
		tmp++;
	}
	while (!now.a[now.n]) now.n--;
}

void NTT(gj &now, int op) {
	for (int i = 0; i < limit; i++)
		if (i < an[i]) swap(now.a[i], now.a[an[i]]);
	for (int mid = 1; mid < limit; mid <<= 1) {
		ll Wn = ksm(op == 1 ? G : Gv, (mo - 1) / (mid << 1));
		for (int R = (mid << 1), j = 0; j < limit; j += R) {
			ll w = 1;
			for (int k = 0; k < mid; k++, w = w * Wn % mo) {
				ll x = now.a[j + k], y = w * now.a[j + mid + k] % mo;
				now.a[j + k] = (x + y) % mo;
				now.a[j + mid + k] = (x - y + mo) % mo;
			}
		}
	}
}

void CHENG(gj &x, gj y) {
	limit = 1; ln = 0;
	while (limit <= x.n + y.n) {
		limit <<= 1;
		ln++;
	}
	for (int i = 0; i < limit; i++)//高精乘用 NTT 加速
		an[i] = (an[i >> 1] >> 1) | ((i & 1) << (ln - 1));
	NTT(x, 1); NTT(y, 1);
	for (int i = 0; i < limit; i++)
		x.a[i] = (x.a[i] * y.a[i]) % mo;
	NTT(x, -1);
	ll limv = ksm(limit, mo - 2);
	for (int i = 0; i <= x.n + y.n + 1; i++)
		x.a[i] = (x.a[i] * limv) % mo;
	for (int i = 0; i <= x.n + y.n + 1; i++) {//记得进位
		x.a[i + 1] += x.a[i] / 10;
		x.a[i] %= 10;
	}
	x.n = x.n + y.n + 1;
	while (!x.a[x.n]) x.n--;
}

int main() {
	Gv = ksm(G, mo - 2);
		
	scanf("%s", &s);
	sn = strlen(s) - 1;
	
	if ((s[sn] - '0') & 1) {
		printf("0"); return 0;
	}
	n.n = sn;
	for (int i = 0; i <= sn; i++)
		n.a[sn - i] = s[i] - '0';
	
	x = n;
	x.a[0] += 4;
	int tmp = 0;
	while (x.a[tmp] > 9) {
		x.a[tmp + 1] += x.a[tmp] / 10;
		x.a[tmp] %= 10; tmp++;
	}
	if (tmp > x.n) x.n = tmp;
	chu(x, 2);//得到 x=(n+4)/2
	x1 = x2 = x3 = x;
	jian(x1, 1); jian(x2, 2); jian(x3, 3);//得到 x-1,x-2,x-3
	
	CHENG(x1, x2);
	CHENG(x1, x2);
	CHENG(x1, x3);
	chu(x1, 12);//得到 ans=(x-1)(x-2)^2(x-3)/12
	
	for (int i = x1.n; i >= 0; i--)
		printf("%lld", x1.a[i]);
	
	return 0;
}