bzoj1013: [JSOI2008]球形空间产生器sphere（高斯消元）

　　终于学了高斯消元法，竟然比想象中的简单很多...（这名字逼格好高QAQ

　　学的是Gauss-Jordan，虽然很短但是据说有点慢，无所谓啦233

　　高斯消元法过程：第i行所有系数除以第i项系数，使第i项系数为1，再与其他行相减把其他行第i项系数消为0。这样第i行的等式右边就是第i个未知数的值。

　　圆上各点到圆心距离相等。。。设圆心坐标为(x[1],x[2],x[3]...x[n])

　　列出方程组

　　

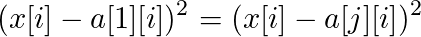
　　化简得

　　

　　然后就可以用高斯消元了

#include<bits/stdc++.h>
#define ll long long 
using namespace std;
const double eps=1e-6;
int n,to;
double x;
double f[21],a[21][21];
void gauss()
{
    for(int i=1;i<=n;i++)
    {
        for(to=i;to<=n;to++)if(fabs(a[to][i])>eps)break;
        if(to!=i)for(int j=1;j<=n+1;j++)swap(a[i][j],a[to][j]);
        x=a[i][i];for(int j=1;j<=n+1;j++)a[i][j]/=x;
        for(int j=1;j<=n;j++)
        if(i!=j)
        {
            x=a[j][i];
            for(int k=1;k<=n+1;k++)
            a[j][k]-=x*a[i][k];
        }
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%lf",&f[i]);
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    {
        scanf("%lf",&x);
        a[i][j]=2*(x-f[j]);
        a[i][n+1]+=x*x-f[j]*f[j];
    }
    gauss();
    for(int i=1;i<n;i++)printf("%.3lf ",a[i][n+1]);
    printf("%.3lf
",a[n][n+1]);
    return 0;
}