题意:
有n个点的一棵树,两种操作:
1. a到b的路径上,给一个y,对于路径上每一条边,进行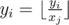 操作,问最后的y;
操作,问最后的y;
2. 修改某个条边p的值为c
思路:
链上操作的问题,想树链剖分和LCT,对于第一种操作,因为是向下取整,考虑y除以路径上所有边乘积,即;对于第二种操作,就是线段树上的单点更新。因为给的是边的序号,首先每个id能知道对应的边值(ide[])和连接的点(idv[])。还有乘法溢出的处理,写成函数方便多了。
另外:
1. 用dfn来替换dep完全没有问题,那以后就用dfn吧。2. 第二次DFS,要先去重儿子的路,这样dfn[son[u]]=dfn[u]+1,son数组也省了。3. 代码debug水平有待提升。4. 树的建图用vector就行了,不需要邻接表(n-1条边)。
#include <bits/stdc++.h>
typedef long long ll;
const int N = 2e5 + 5;
const ll INF = 2e18;
std::vector<std::pair<int, int> > edges[N];
int n, m;
int dfn[N], fa[N], son[N], sz[N], belong[N];
ll ide[N];
int idv[N];
int tim;
inline ll mul(ll a, ll b) {
if (a != 0 && b > INF / a) return INF;
return a * b;
}
void DFS2(int u, int chain) {
dfn[u] = ++tim;
belong[u] = chain;
if (son[u] != 0) {
DFS2 (son[u], chain);
}
for (auto e: edges[u]) {
int v = e.first;
if (v == fa[u] || v == son[u]) continue;
DFS2 (v, v);
}
}
void DFS1(int u, int pa) {
sz[u] = 1;
fa[u] = pa;
for (auto e: edges[u]) {
int v = e.first, id = e.second;
if (v == pa) continue;
idv[id] = v;
DFS1 (v, u);
if (sz[v] > sz[son[u]]) son[u] = v;
sz[u] += sz[v];
}
}
#define lson l, mid, o << 1
#define rson mid + 1, r, o << 1 | 1
ll val[N<<2];
void push_up(int o) {
val[o] = mul (val[o<<1], val[o<<1|1]);
}
void tree_updata(int p, ll c, int l, int r, int o) {
if (l == r) {
val[o] = c;
return ;
}
int mid = l + r >> 1;
if (p <= mid) tree_updata (p, c, lson);
else tree_updata (p, c, rson);
push_up (o);
}
ll tree_query(int ql, int qr, int l, int r, int o) {
if (ql <= l && r <= qr) {
return val[o];
}
int mid = l + r >> 1;
ll ret = 1;
if (ql <= mid) ret = mul (ret, tree_query (ql, qr, lson));
if (qr > mid) ret = mul (ret, tree_query (ql, qr, rson));
return ret;
}
ll query(int a, int b) {
ll ret = 1;
int p = belong[a], q = belong[b];
while (p != q) {
if (dfn[p] < dfn[q]) {
std::swap (p, q);
std::swap (a, b);
}
ret = mul (ret, tree_query (dfn[p], dfn[a], 1, n, 1));
a = fa[p];
p = belong[a];
}
if (dfn[a] < dfn[b]) std::swap (a, b);
if (a != b) {
ret = mul (ret, tree_query (dfn[son[b]], dfn[a], 1, n, 1));
}
return ret;
}
void modify(int id, ll c) {
tree_updata (dfn[idv[id]], c, 1, n, 1);
}
void prepare() {
DFS1 (1, 0);
tim = 0;
DFS2 (1, 1);
for (int i=1; i<n; ++i) {
tree_updata (dfn[idv[i]], ide[i], 1, n, 1);
}
}
int main() {
scanf ("%d%d", &n, &m);
for (int i=1; i<n; ++i) {
int u, v;
ll w;
scanf ("%d%d%I64d", &u, &v, &w);
ide[i] = w;
edges[u].push_back ({v, i});
edges[v].push_back ({u, i});
}
prepare ();
for (int i=0; i<m; ++i) {
int t, a, b;
ll c;
scanf ("%d%d", &t, &a);
if (t == 1) {
scanf ("%d%I64d", &b, &c);
printf ("%I64d
", c / query (a, b));
} else {
scanf ("%I64d", &c);
modify (a, c);
}
}
return 0;
}