猫和狗
题目描述
小 (k) 同学正在玩一个游戏,在游戏中他扮演了一个马戏团的老板,现在小 (k) 同学需要利用马戏团中的 (A) 只猫和 (B) 只狗举办一次表演,表演之前他让观众进行了投票,投票的类容是:我想看到第___号猫/狗的表演,不想看到第___号猫/狗的表演。
注意到每个观众都是更喜欢猫或更喜欢狗,所以两个空后面一定会被勾上不同的内容。喜欢猫的观众会在第一空后面选择猫,第二空后面选择狗;反之就会在第一空后面选择狗,第二空后面选择猫。
对于每一个观众,只有当他投票的内容都被满足了(即他想看到的动物出场表演,他不想看到的动物不参与表演)的时候,他才会来看表演。当然啦,看表演是要付门票钱的,作为马戏团的老板,小 (k) 自然是希望来的人越多越好了。他想找到一个安排动物表演的方案,使得来看表演的观众尽量多。
输入格式
第 (1) 行 (3) 个正整数 (n,m,k),分别表示猫、狗和观众的数量
第 (2 sim k+1) 行,每行描述了一个观众的投票内容。
首先输入一个字符 (C) 或 (D) 紧接着是一个数字,表示某个观众想看到的动物,然后是一个空格隔开,接下去又是一个 (C) 或 (D) 加上一个数字,表示这个观众不想看到的动物,同一行中一定不会出现两个 (C) 或两个 (D) 。
输出格式
输出一行一个正整数,表示小 (k) 在最优的安排下可以吸引多少观众来看表演。
样例
样例输入
1 2 4
C1 D1
C1 D1
C1 D2
D2 C1
样例输出
3
数据范围与提示
对于 (25\%) 的数据:(n,mleq 10,kleq 25);
对于 (100\%) 的数据:(n,mleq 300,kleq 500) 。
思路
很明显的二分图,我们将猫狗依次编号,将喜欢 (i) 号动物的人与讨厌 (i) 号动物的人建边,求出最大匹配,用总人数减去最大匹配数的 (frac{1}{2}) 便是答案。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 50, INF = 0x3f3f3f3f;
inline int read(){
int x = 0, w = 1;
char ch;
for (; ch < '0' || ch > '9'; ch = getchar()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch =getchar()) x = x * 10 + ch - '0';
return x * w;
}
int n, m, k;
struct Node{
int like, hate;
}a[maxn];
int e[maxn][maxn];
bool vis[maxn];
int girls[maxn];
int ans;
bool Find(int x){//匈牙利
for (int i = 1; i <= k; i++) {
if (e[x][i] && !vis[i]) {
vis[i] = 1;
if (!girls[i] || Find(girls[i])) {
girls[i] = x;
return 1;
}
}
}
return 0;
}
int main(){
n = read(), m = read(), k = read();
for (int i = 1; i <= k; i++) {
char x, y;
int h, s;
cin >> x >> h >> y >> s;
if (x == 'D') h += n + m;//重新编号
if (y == 'D') s += n + m;
a[i].like = h;
a[i].hate = s;
}
for (int i = 1; i <= k; i++) {
for (int j = 1; j <= k; j++) {
if (a[i].like == a[j].hate) {
e[i][j] = 1;//建双向边
e[j][i] = 1;
}
}
}
for (int i = 1; i <= k; i++) {
memset(vis, 0, sizeof vis);
if (Find(i)) ans++;
}
printf("%d
", k - ans / 2);
return 0;
}
旋转子段
题目描述
(ZYL) 有 (N) 张牌编号分别为 (1),(2),(......),(N) 。
他把这 (N) 张牌打乱排成一排,然后他要做一次旋转使得旋转后固定点尽可能多。
如果第 (i) 个位置的牌的编号为 (i),我们就称之为固定点。旋转可以被认为是将其中的一个子段旋转 (180) 度,这意味着子段的第一张牌和最后一张牌交换位置,以及第二张牌和倒数第二张牌交换位置,等等。写一个程序,找到旋转子段(子段长度可以为 (1) )。
输入格式
第一行包含一个整数 (N(1leq Nleq 100000)) 。
第二行有 (N) 个数,第 (i) 个数表示旋转之前第 (i) 个位置的牌的编号。
输出格式
找到固定点最多的旋转所选的子段,输出旋转之后固定点的个数。
样例
样例 #1
rotate.in
4
3 2 1 4
rotate.out
4
样例 #2
rotate.in
2
1 2
rotate.out
2
数据范围与提示
样例解释
在样例 (1) 中,只需要旋转的子段 ([3,2,1]),将排列变成 (1 : 2 : 3 : 4),旋转后所有的牌都为固定点。答案为 (4) 。
在样例 (2) 中,所有的牌已经在固定点,旋转子段 ([1]) 或者子段 ([2]),答案为 (2) 。
数据范围
(30\%) 的数据满足:(Nleq 500);
(60\%) 的数据满足:(Nleq 5000);
(100\%) 的数据满足:(1leq Nleq 500000) 。
思路
我们仔细研究这个数列,会发现以下性质:
-
当 (a[i] eq i) 时,把 (a[i]) 翻转为固定点的最小区间为 ([L,R](L=min(a[i],i),R=max(a[i],i))),可以扩展到 ([L+1,R+1],[L+2,R+2],......[L+k,R+k]) ,区间长度 (len=abs(a[i]-i+1)) 。
-
当一些数 (a[i]+i) 的数值相等时,必定有一个翻转范围使这几个数都成为固定点,例如:
很明显有 (5,4,3,2) 的 (a[i]+i) 的值相同,可以找到 ([2,5]) 的翻转区间,使这 (4) 个数都成为固定数。
根据以上性质,我们可以用一个 (vector),将 (a[i]+i) 值相同的 (i) 放到一个队列里,然后按照区间长度排序,将区间内可得的固定数加上区间外原来就有的固定数,取个 (max),就是答案。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 50, INF = 0x3f3f3f3f;
inline int read(){
int x = 0, w = 1;
char ch;
for (; ch < '0' || ch > '9'; ch = getchar()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch =getchar()) x = x * 10 + ch - '0';
return x * w;
}
int n;
int a[maxn];
int L[maxn], R[maxn];
vector <int> vec[maxn];
int ans;
int p;
bool cmp(int x, int y){//区间从小到大排序
return abs(p - 2 * x + 1) < abs(p - 2 * y + 1);
}
void H2SO4(){
for (int i = 2; i <= 2 * n; i++) {
if (!vec[i].empty()) {
p = i;
sort(vec[i].begin(), vec[i].end(), cmp);
for (int j = 0; j < vec[i].size(); j++) {
int l = vec[i][j];
int r = i - l;
if (l > r) swap (l, r);
ans = max(ans, L[l - 1] + R[r + 1] + j + 1);
}
}
}
}
int main(){
n = read();
for (int i = 1; i <= n; i++) {
a[i] = read();
L[i] = L[i - 1];//统计i左边的固定数
if (a[i] == i) {
L[i] = L[i - 1] + 1;
}
vec[a[i] + i].push_back(i);
}
for (int i = n; i >= 1; i--) {
R[i] = R[i + 1];//统计i右边的固定数
if (a[i] == i) {
R[i] = R[i + 1] + 1;
}
}
H2SO4();
printf("%d
", ans);
return 0;
}
走格子
题目描述
(CYJ) 想找到他的小伙伴 (FPJ),(CYJ) 和 (FPJ) 现在位于一个房间里,这个房间的布置可以看成一个 (N) 行 (M) 列的矩阵,矩阵内的每一个元素会是下列情况中的一种:
(1.) 障碍区域—这里有一堵墙(用 ‘ (#) ’表示)。
(2.) 这是 (CYJ) 最开始在的区域(用‘ (C) ’表示)。
(3.) 这是 (FPJ) 在的区域(用‘ (F) ’表示)。
(4.) 空区域(用‘ (.) ’表示)。
(CYJ) 携带了一个所谓传送枪的东西,这是一把可以创造传送门的枪械,在每一次行动中,他可以选择下列操作中的一项:
(1.) 移向一个相邻的格子中(上,下,左,右,不能移到墙在的格子里).这个操作要消耗一个单位的时间。
(2.) 转向一个墙(不需要相邻,只需面向即可),向其发射传送门,传送门会留在墙内面向你的地方(至多只能同时存在两扇传送门),若墙上已经有两扇传送门,而你发射了第三扇,那么最初发射的那一扇会消失。同时,你无法在一个位置制造两扇传送门(这个操作不会耗费时间)。
(3.) 如果他与一块墙壁相邻且面前有一扇传送门,那么他可以移动到另一扇传送门前方的格子。这个操作会耗费一个单位的时间。
(CYJ) 想要知道自己最少需要多少时间才能够从起点(‘ (C) ’)到达终点(‘ (F) ’)。
请注意:我们保证地图边缘会是一圈墙壁且一定存在 ‘ (C) ’,‘ (F) ’。
输入格式
第一行输入两个正整数 (N) 和 (M,(4leq N,Mleq 500)),表示地图大小。
接下来的 (N) 行每行一个长度为 (M) 的字符串,表示地形。
输出格式
你需要输出最少的到达终点的时间,如果不能到达请输出” (no) ”。
样例
样例 #1
cell.in
4 4
####
#.F#
#C.#
####
cell.out
2
样例 #2
cell.in
6 8
########
#.##..F#
#C.##..#
#..#...#
#.....##
########
cell.out
4
样例 #3
cell.in
4 5
#####
#C#.#
###F#
#####
cell.out
no
数据范围与提示
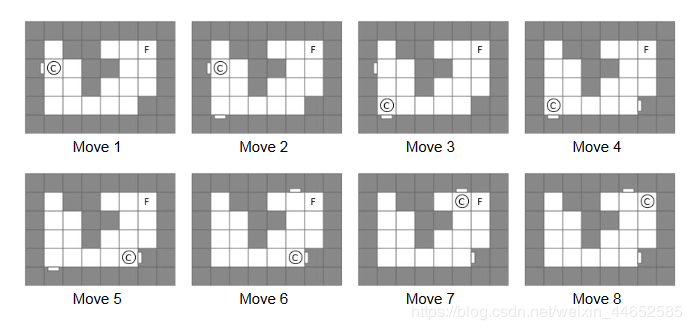
样例 (2) 解释
- 从 (C) 点 ((3,2)) 开始,我们首先向左发射传送门,再向下发射传送门,向左进入传送门,到达 ((5,2)),向右发射传送门,向下进入传送门,到达 ((5,6)) ,向上发射传送门,向右进入传送门,到达 ((2,6)) ,向右移动,到达 (F) 。
(50\%) 的数据满足:(4leq N,Mleq 15);
(100\%) 的数据满足:(4leq N,Mleq 500);
思路
依旧是二维转为一维的图论,不过只是多了个传送门,其实很好处理。
我们从一个点找到他四个方向最近的墙,从那个墙可以到其他三个墙中任意一个,建边即可,注意建的是原来的起点到三个墙的边,而不是那个墙到其他三个墙的边。
最后你找四个墙 (for) 循环和 (BFS) 都无所谓。
最短路跑 (DIJ) 和 (SPFA) 也都无所谓,不提倡用 (SPFA),它跑稠密图很慢。
我跑的 (SPFA) 加 (for)循环,慢上加慢,而且 (W80),不知道哪里错了,如果大家有发现请评论区指出。
代码
正解
#include <bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, w = 1;
char ch;
for(; ch > '9' || ch < '0'; ch = getchar()) if(ch == '-') w = -1;
for(; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
return x * w;
}
const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, 1, 0, -1};
const int maxn = 550;
int n, m, begin, end;
char a[maxn][maxn];
int b[maxn][maxn];
struct E{
int to, nxt, w;
}edge[maxn * maxn * 10];
int head[maxn * maxn * 10], tot;
inline void add(int u, int v, int w){
edge[++tot].to = v;
edge[tot].nxt = head[u];
edge[tot].w = w;
head[u] = tot;
}
queue<pair<int, int> > que;
inline void BFS(){
while(!que.empty()){
int x = que.front().first, y = que.front().second;
que.pop();
for(int i = 0; i < 4; i++){
int xx = x + dx[i];
int yy = y + dy[i];
if(a[xx][yy] == '.' && !b[xx][yy]){
b[xx][yy] = b[x][y] + 1;
que.push(make_pair(xx, yy));
}
}
}
}
inline int change(int i, int j){
return (i - 1) * m + j;
}
int above[maxn][maxn], under[maxn][maxn], leftt[maxn][maxn], rightt[maxn][maxn];
inline void init(){
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++){
if(a[i][j] == '#') continue;
if(a[i - 1][j] == '#') above[i][j] = change(i, j);
else above[i][j] = above[i - 1][j];
if(a[i][j - 1] == '#') leftt[i][j] = change(i, j);
else leftt[i][j] = leftt[i][j - 1];
}
for(int i = n; i >= 1; i--)
for(int j = m; j >= 1; j--){
if(a[i][j] == '#') continue;
if(a[i + 1][j] == '#') under[i][j] = change(i, j);
else under[i][j] = under[i + 1][j];
if(a[i][j + 1] == '#') rightt[i][j] = change(i, j);
else rightt[i][j] = rightt[i][j + 1];
}
}
inline void build(){
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(a[i][j] == '#') continue;
if(a[i + 1][j] == '.'){
add(change(i, j) ,change(i + 1, j), 1);
add(change(i + 1, j), change(i, j), 1);
}
if(a[i][j + 1] == '.'){
add(change(i, j), change(i, j + 1), 1);
add(change(i, j + 1), change(i, j), 1);
}
if(leftt[i][j] != change(i, j)){
add(change(i, j), leftt[i][j], b[i][j]);
}
if(rightt[i][j] != change(i, j)){
add(change(i, j), rightt[i][j], b[i][j]);
}
if(above[i][j] != change(i, j)){
add(change(i, j), above[i][j], b[i][j]);
}
if(under[i][j] != change(i, j)){
add(change(i, j), under[i][j], b[i][j]);
}
}
}
}
struct Node{
int dis, pos;
Node(int a, int b){
pos = a;
dis = b;
}
inline bool operator < (const Node &x) const {
return dis > x.dis;
}
};
priority_queue<Node> q;
int dis[maxn * maxn * 10];
bool vis[maxn * maxn * 10];
inline void Dij(int x){
memset(dis, 0x3f, sizeof dis);
dis[x] = 0;
q.push(Node(x, 0));
while(!q.empty()){
Node tmp = q.top();
q.pop();
int u = tmp.pos;
int w = tmp.dis;
if(vis[u]) continue;
vis[u] = 1;
for(int i = head[u]; i; i = edge[i].nxt){
int v = edge[i].to;
if(dis[v] > w + edge[i].w){
dis[v] = w + edge[i].w;
q.push(Node(v, dis[v]));
}
}
}
}
signed main(){
n = read(), m = read();
for(int i = 1; i <= n; i++){
scanf("%s", a[i] + 1);
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(a[i][j] == 'C'){
begin = change(i, j);
a[i][j] = '.';
}else if(a[i][j] == 'F'){
end = change(i, j);
a[i][j] = '.';
}else if(a[i][j] == '#'){
que.push(make_pair(i, j));
}
}
}
BFS();
init();
build();
Dij(begin);
if(dis[end] == 0x3f3f3f3f) puts("no");
else printf("%d
", dis[end]);
return 0;
}
我的W80
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e7 + 50, INF = 0x3f3f3f3f;
inline int read(){
int x = 0, w = 1;
char ch;
for (; ch < '0' || ch > '9'; ch = getchar()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch =getchar()) x = x * 10 + ch - '0';
return x * w;
}
int n, m;
int from, to;
int pan[550][550];
int dx[4] = {1, 0, 0, -1};
int dy[4] = {0, 1, -1, 0};
struct Edge{
int to, next, w;
}e[maxn];
int tot, head[maxn];
void Add(int u, int v, int w){
e[++tot].to = v;
e[tot].w = w;
e[tot].next = head[u];
head[u] = tot;
}
int dis[maxn], vis[maxn];
void SPFA(int x) {
memset(dis, 0x3f, sizeof dis);
memset(vis, 0, sizeof vis);
dis[x] = 0;
queue <int> q;
q.push(x);
while (!q.empty()) {
int u = q.front();
q.pop();
for (register int i = head[u]; i; i = e[i].next) {
int v = e[i].to;
if (dis[v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
if (!vis[v]) {
vis[v] = 1;
q.push(v);
}
}
}
}
}
int main(){
n = read(), m = read();
for (register int i = 1; i <= n; i++) {
char x[550];
scanf("%s", x);
for (register int j = 0; j < m; j++) {
if (x[j] == '#') {
pan[i][j + 1] = 1;
}else if (x[j] == 'C') {
from = (i - 1) * m + j + 1;
}else if (x[j] == 'F') {
to = (i - 1) * m + j + 1;
}
}
}
for (register int i = 1; i <= n; i++) {
for (register int j = 1; j <= m; j++) {
int u = (i - 1) * m + j;
for (register int k = 0; k <= 3; k++) {
int xx = i + dx[k], yy = j + dy[k];
int v = (xx - 1) * m + yy;
if(pan[xx][yy] == 1) continue;
Add(u, v, 1);
}
}
}
for (register int i = 1; i <= n; i++) {
for (register int j = 1; j <= m; j++) {
if (i == 1 || j == 1 || i == n || j == m) continue;
if (pan[i][j] == 1) continue;
int u = (i - 1) * m + j;
int x1 = i - 1;
int d1 = 0;
while (!pan[x1][j]) {//上面最近的墙
x1--;
d1++;
}
x1++;
int v1 = (x1 - 1) * m + j;
int x2 = i + 1;
int d2 = 0;
while (!pan[x2][j]) {//下面最近的墙
x2++;
d2++;
}
x2--;
int v2 = (x2 - 1) * m + j;
int y1 = j - 1;
int d3 = 0;
while (!pan[i][y1]) {//左面最近的墙
y1--;
d3++;
}
y1++;
int v3 = (i - 1) * m + y1;
int y2 = j + 1;
int d4 = 0;
while (!pan[i][y2]) {//右面最近的墙
y2++;
d4++;
}
y2--;
int v4 = (i - 1) * m + y2;
int d = min(min(d1, d2), min(d3, d4));
if (d == d1) {
Add(u, v1, d);
Add(u, v2, d + 1);
Add(u, v3, d + 1);
Add(u, v4, d + 1);
}else if (d == d2) {
Add(u, v2, d);
Add(u, v1, d + 1);
Add(u, v3, d + 1);
Add(u, v4, d + 1);
}else if (d == d3) {
Add(u, v3, d);
Add(u, v1, d + 1);
Add(u, v2, d + 1);
Add(u, v4, d + 1);
}else if (d == d4) {
Add(u, v4, d);
Add(u, v1, d + 1);
Add(u, v2, d + 1);
Add(u, v3, d + 1);
}
}
}
SPFA(from);
if (dis[to] == INF) puts("no");
else printf("%d
",dis[to]);
return 0;
}
柱状图
题目描述
(WTH) 获得了一个柱状图,这个柱状图一共有 (N) 个柱子,最开始第 (i) 根柱子的高度为 (x_i),他现在要将这个柱状图排成一个屋顶的形状,屋顶的定义如下:
-
屋顶存在一个最高的柱子,假设为 (i),最终高度为 (h_i),它是所有柱子之中最高的。
-
第 (j) 根柱子的高度为 (h_j=h_i-|i-j|),但这个高度必须大于 (0),否则就是不合法的。
可以对一个柱子做的操作只有将其高度加一或减一,(WTH) 正忙着享受自己的人赢生活于是他将把这个柱状图变成屋顶的任务交给了你。
你需要求出最少进行多少次操作才能够把这个柱状图变成一个屋顶形状。
输入格式
第一行包含一个正整数 (N(1leq Nleq 100000)) 。
第二行包含 (N) 个用空格隔开的正整数,表示 (x_i),含义如题面。
输出格式
输出最少进行多少个操作才能够把这个柱状图变成屋顶的形状。
样例
样例输入 #1
column.in
4
1 1 2 3
样例输出 #1
column.out
3
样例输入 #2
column.in
5
4 5 7 2 2
样例输出 #2
column.out
4
数据范围与提示
样例的解释
例一升高 (2,3,4) 号柱子一个单位高度是操作最少的方法之一,最高处为第四个柱子。例二降低第三根柱子三个高度,升高第四个柱子一个高度。最高处为第 (2) 个柱子。
数据范围
(30\%) 的数据满足:(1leq Nleq 100) 。
(60\%) 的数据满足:(1leq Nleq 5000) 。
(100\%) 的数据满足:(1leq Nleq 100000),(1leq h_ileq 10^9) 。
思路
三分法
待更新~~~