
这道题就是维护两个优先队列 之前做过一道很像的题目
这道题是维护两个队列 上面一个队列表示的是还未买进来的东西 另一个是后悔队列
先说他是怎么做的
每次遇到一个元素 将他与两个队头作差 选择差更大的 如果是上面更优 那么就将上面队列队首弹出 表示一定会选择它 他会做出贡献
然后再将这个新元素压入下面的队列 供以后后悔使用
那么如果弹出队首就表示我买了队首 再将现在这个东西卖出去
若是弹出下面队列的队首 则表示之前买的东西不买了 换成买这个 贡献加上作差的值 再将下面队列的队首压入上面队列 表示它可以重新被买了
代码
#include <bits/stdc++.h> #define oo 1e9 using namespace std; int n; struct node { int val; bool operator < (const node & a) const { return val > a.val; } }; priority_queue<node>Q1, Q2; int read( ) { int t = 1, ans = 0; char x; x = getchar( ); while(x < '0' || x > '9') { if(x == '-') t = -1; x = getchar( ); } while(x >= '0' && x <= '9') { ans = ans * 10 + x - '0'; x = getchar( ); } return ans * t; } void Solve( ) { n = read( ); long long ans = 0; for(int i = 1;i <= n;i ++) { node a; a.val = read( ); int cmp1 = -oo, cmp2 = -oo; if(! Q1.empty( )) cmp1 = a.val - Q1.top( ).val; if(! Q2.empty( )) cmp2 = a.val - Q2.top( ).val; if(cmp1 >= cmp2 && cmp1 > 0) { ans += 1ll * cmp1; Q1.pop( ); Q2.push(a); } else if(cmp2 > cmp1 && cmp2 > 0){ ans += 1ll * cmp2; node u = Q2.top( ); Q2.pop( ); Q1.push(u); Q2.push(a); } else Q1.push(a); } printf("%lld ",ans); } int main( ) { freopen("trade.in","r",stdin); freopen("trade.out","w",stdout); Solve( ); }

代码
#include <bits/stdc++.h> using namespace std; const long long MOD = 1e9 + 7; const int L = 1e5; const int N = 1e5 + 5; const long long inv2 = 5e8 + 4; long long n, m, fac[N], rfac[N], blo[N]; long long Ans[N]; int Case, T; struct data { long long n, m; int id; data(long long n = 0, long long m = 0, long long id = 0): n(n), m(m), id(id) {} }q[N]; bool cmp(const data & a, const data & b) { return blo[a.n] == blo[b.n] ? a.m < b.m : a.n < b.n; } long long fast_pow(long long a, long long b) { long long ans = 1; for(; b; b >>= 1, a = a * a % MOD) if(b & 1) ans = ans * a % MOD; return ans; } void Init( ) { scanf("%d",& Case); scanf("%d",& T); fac[0] = 1; rfac[0] = 1; for(int i = 1;i <= L;i ++) { fac[i] = 1ll * fac[i - 1] * i % MOD; rfac[i] = fast_pow(fac[i], MOD - 2); } for(int i = 1;i <= T;i ++) { scanf("%lld%lld",& n,& m); q[i] = data(n, m, i); } for(int i = 1;i <= L;i ++) blo[i] = i / 300 + 1; sort(q + 1, q + T + 1, cmp); } long long C(int n, int m) { if(m > n) return 0; return 1ll * fac[n] * rfac[m] % MOD * rfac[n - m] % MOD; } void Solve( ) { long long ans = 0; for(int i = 0;i <= q[1].m;i ++) ans = (ans + 1ll * C(q[1].n, i)) % MOD; Ans[q[1].id] = ans; long long n = q[1].n, m = q[1].m; for(int i = 2;i <= T;i ++) { while(q[i].m < m) { ans = (ans - C(n, m) + MOD) % MOD; m --; } while(q[i].n > n) { ans = (ans * 2 - C(n, m) + MOD) % MOD; n ++; } while(q[i].m > m) { m ++; ans = (ans + C(n, m)) % MOD; } while(q[i].n < n) { n --; ans = 1ll * (ans + 1ll * C(n, m) + MOD) % MOD * inv2 % MOD; } Ans[q[i].id] = ans; } for(int i = 1;i <= T;i ++) printf("%lld ",Ans[i]); } int main( ) { freopen("sum.in","r",stdin); freopen("sum.out","w",stdout); Init( ); Solve( ); }


这道题真的挺难的...
求某段区间的被覆盖格子数还是挺简单的 std用的是差分 我用的线段树 竖向建一颗 每次如果是横向覆盖就直接单点加上贡献 否则是区间加一
重点是统计从第一行到某一行连通块的个数
开两个$vecor$一个代表列 一个代表行 一个保存以该行为矩形上边界的矩形 另一个保存以该列为矩形左边界的矩形
目的是方便以后统计连通块的个数 对于每个矩形 我们统计他的右边界和下边界与哪些矩形相连 因为如果他左边与上面与别的矩形相连 他会被统计到的
所以考虑怎么通过统计别的矩形来得到现在这一行到第一行的连通块个数
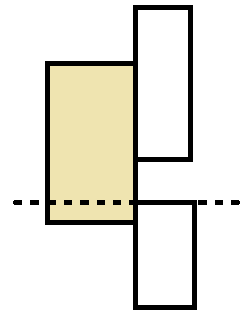
对于这个米色的矩形 我们考虑和他相连的右边的矩形 设该矩形的右边界为$s$ 则判断左边界在$s + 1$ 位置的矩形
通过$upperbound - 1$可以找到第一个和他相连的矩形 然后将他们两个连边 然后一个一个向前搞 直到他们不相连为止
连边是对于每一行存储的 表示这一行产生多少连边
在相连的两个矩形之间 我们选择上边界更下面的存边 原因等会儿再说
然后枚举行数 每到一行矩形总数就加上这一行的矩形数 然后再减去这一行的连边数 因为每多连一条边 就少一个矩形
因为在统计答案时 我们是边走边加上矩形的个数 如果将连边存在上面 那么这条边就会在还没有统计到相连的靠下面那个矩形被统计 答案会变少
所以边走边统计答案就可以了 不得不说 这道题完美运用了stl... 简直让我这个老年人叹为观止
代码
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 1e5 + 5; ll f[4 * N], num[N], tag[4 * N]; int n, m, id, q, k, a[103][103], fa[N], idc, ans[N], sum; int zl[4][4] = {{0, 1},{0, -1},{1, 0},{-1, 0}}; bool vis[103][103]; vector<pair<int, int> >G[N * 10]; struct Data { int lx, rx, ly, ry; Data(int lx = 0, int ly = 0, int rx = 0, int ry = 0): lx(lx), ly(ly), rx(rx), ry(ry) {} }A[N]; struct node { int id, l, r; node(int id = 0, int l = 0, int r = 0): id(id), l(l), r(r) {} }; vector<node>row[N], col[N]; bool operator < (const node & a, const node & b) { return a.l < b.l || (a.l == b.l && a.r < b.r); } void push_down(int o, int l, int r) { int mid = l + r >> 1; if(tag[o] != 0) { f[2 * o] += tag[o] * (mid - l + 1); f[2 * o + 1] += tag[o] * (r - mid); tag[2 * o] += tag[o]; tag[2 * o + 1] += tag[o]; tag[o] = 0; } } void update(int o) { f[o] = f[2 * o] + f[2 * o + 1]; } void modify(int o, int l, int r, int L, int R, int del) { if(l >= L && r <= R) { f[o] += del * (r - l + 1); tag[o] += del; return ; } push_down(o, l, r); int mid = l + r >> 1; if(L <= mid) modify(2 * o, l, mid, L, R, del); if(mid < R) modify(2 * o + 1, mid + 1, r, L, R, del); update(o); } ll query(int o, int l, int r, int L, int R) { if(l >= L && r <= R) return f[o]; push_down(o, l, r); int mid = l + r >> 1; ll ans = 0; if(L <= mid) ans += query(2 * o, l, mid, L, R); if(mid < R) ans += query(2 * o + 1, mid + 1, r, L, R); return ans; } int read( ) { int t = 1, ans = 0; char x; x = getchar( ); while(x < '0' || x > '9') { if(x == '-') t = -1; x = getchar( ); } while(x >= '0' && x <= '9') { ans = ans * 10 + x - '0'; x = getchar( ); } return ans * t; } int find_fa(int u) { return fa[u] == u ? u : find_fa(fa[u]); } void merge(int u, int v) { int fa1 = find_fa(u), fa2 = find_fa(v); if(fa1 == fa2) return ; fa[fa1] = fa2; idc ++; } void Init( ) { scanf("%d",& id); scanf("%d%d%d%d",& n,& m,& k,& q); for(int i = 1;i <= k;i ++) fa[i] = i; for(int i = 1;i <= k;i ++) { int lx, ly, rx, ry; lx = read( ), ly = read( ), rx = read( ), ry = read( ); A[i] = Data(lx, ly, rx, ry); row[lx].push_back(node(i, ly, ry)); col[ly].push_back(node(i, lx, rx)); if(lx == rx) { int del = ry - ly + 1; modify(1, 1, n, lx, lx, del); } else { modify(1, 1, n, lx, rx, 1); } } for(int i = 1;i <= n;i ++) sort(row[i].begin( ), row[i].end( )); for(int i = 1;i <= m;i ++) sort(col[i].begin( ), col[i].end( )); for(int i = 1;i <= k;i ++) { int down = A[i].rx + 1; if(down <= n && row[down].size( )) { int pos = upper_bound(row[down].begin( ), row[down].end( ), node(0, A[i].ry, m + 1)) - row[down].begin( ) - 1; for(; pos >= 0 && row[down][pos].r >= A[i].ly; pos --) { G[down].push_back(make_pair(i, row[down][pos].id)); } } down = A[i].ry + 1; if(down <= m && col[down].size( )) { int pos = upper_bound(col[down].begin( ), col[down].end( ), node(0, A[i].rx, n + 1)) - col[down].begin( ) - 1; for(; pos >= 0 && col[down][pos].r >= A[i].lx; pos --) { G[max(A[i].lx, col[down][pos].l)].push_back(make_pair(i, col[down][pos].id)); } } } sum = 0, idc = 0; for(int i = 1;i <= n;i ++) { sum += row[i].size( ); if(G[i].size( )) { for(int j = 0;j < G[i].size( );j ++) { merge(G[i][j].first, G[i][j].second); } } ans[i] = sum - idc; } } void Solve( ) { while(q --) { int opt, r; opt = read( ), r = read( ); if(opt == 0) printf("%lld ", query(1, 1, n, 1, r)); else printf("%d ", ans[r]); } } int main( ) { freopen("building.in","r",stdin); freopen("building.out","w",stdout); Init( ); Solve( ); }