啊啊啊啊啊啊啊啊考场上差一点就A掉了5555
千里之堤溃于蚁穴……鬼知道最后一步那么显然的柿子我为什么没考虑用上……
观察数据范围可知,出题人期望我们想出一个$O(n)$的做法
当然也有可能是$O(nlogn)$,但是这道题所求的数值与树上每个点的权值有关,
似乎用点分治并不能够解决。
那怎么办?树形dp啊。保证严格$O(n)$。
有了这样的思路,我们先来看第一问,并设计一个可以用一遍dfs计算出数组$b[]$的算法。
各位想必知道,树形dp的基本思想是$"Up and Down"$,
而在最近的比赛和专题中,我们似乎见的大部分这类问题都是先向下dfs到底,再从下往上更新父亲的$dp[]$信息。
但是不要忘了另外一种啊喂……这题先不说从下往上能不能转移,就是起始更新点的初值你都没法$O(n)$以内算……
如果从上往下,用父亲更新儿子就十分好考虑了。
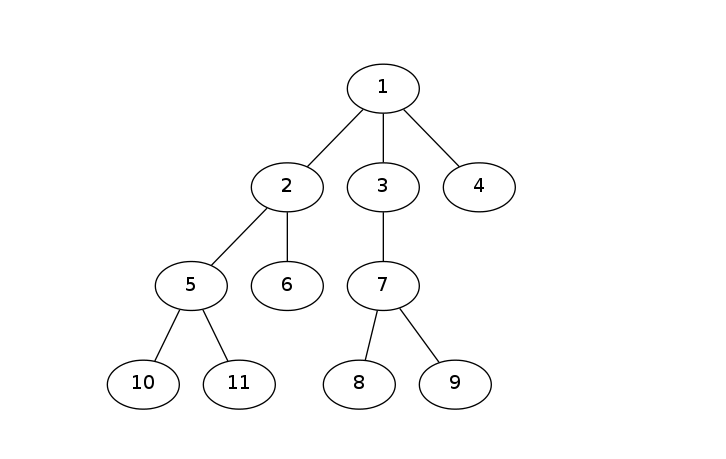
首先,起始点即为根节点,初值用一遍dfs即可算出。
之后考虑怎么转移。假设我们已知$b[2]$,要求它的儿子5的$b[]$,
这时候先来想一下$O(n^2)$的做法,即对于每个节点都跑一遍dfs,它究竟输在了哪里?
显然,有边相连的两点的$b[]$是有关系的,可以通过某种方式转化,而不必每次遍历整棵树进行冗余计算。
从2到5,5的子树(包含5本身)对于$b[]$的贡献都少了1,而5的子树之外的部分对它的贡献都多了1,
再通俗一点,我们把5的子树的贡献写出来:$b[2]=a_5+2*a_{10}+2*a_{11}...(之后就是5的子树之外的部分)$
而$b[5]=a_5*0+1*a_{10}+1*a_{11}+...$
看见没有?系数都少了1!子树外的部分同理。
那么一棵子树的贡献可以看作它内部点的权值和,第一遍dfs的时候就能预处理完毕。设它为$sum[]$。
易得:$b[y]=b[x]-sum[y]+sum[1]-sum[y]=b[x]+sum[1]-sum[y]*2$
第一问解决。
得出上面那个式子之后,第二问也就非常显然了。
我们把$b[x]$移到左侧,得到$b[y]-b[x]=sum[1]-sum[y]*2$
设$dt[y]=b[y]-b[x]$,这玩意相当于题里已经给了可以马上算出来。(当然$dt[1]$肯定求不出来)
先求出每个点的$dt[y]=sum[1]-sum[y]*2$,之后想怎么能够消元。
显然,$b[1]=sum limits _{i=2}^{n} sum[i]$
什么?并不显然?自己手玩去!
然后我们令$total=sum limits _{i=2}^{n}{dt[i]}=(n-1)sum[1]-2*sum limits_{i=2}^{n}{sum[i]}$
发现了什么?因为$b[1]$是已知量,所以可以把$total$减号后面的部分消掉!
$sum[1]$就求出来辣!
又因为所有的$dt[]$都是已知的,所有的$sum[]$就都可以求出来了。
至于$a[]$?再来一遍dfs就行了。
不得不说这道题真的很棒,没有特别难的知识点,整体难度也不太高,
但是很考验选手对于树上信息的处理能力和转化能力,以及基本的数学素养。
部分分也给的很合理,还能考察一下高斯消元。
还在犹豫什么?还不快来%%%% @liu_runda (逃

#include<cstdio> #include<iostream> #include<cstring> using namespace std; const int N=100005; typedef long long ll; int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar(); return x*f; } int to[N<<1],nxt[N<<1],tot,head[N],num[N],sum[N],dep[N]; int dt[N]; int T,n,op; int dp[N]; void add(int x,int y) { to[++tot]=y; nxt[tot]=head[x]; head[x]=tot; } void pre(int x,int deep) { sum[x]=num[x];dep[x]=deep; for(int i=head[x];i;i=nxt[i]) { int y=to[i]; if(dep[y]||y==1)continue; pre(y,deep+1); sum[x]+=sum[y]; } } void dfs(int x) { for(int i=head[x];i;i=nxt[i]) { int y=to[i]; if(dep[y]<dep[x])continue; dp[y]=dp[x]-sum[y]+sum[1]-sum[y]; dfs(y); } } void DFS(int x,int f) { for(int i=head[x];i;i=nxt[i]) { int y=to[i]; if(y==f)continue; dt[y]=dp[y]-dp[x]; DFS(y,x); } } void cacl() { for(int i=1;i<=n;i++) num[i]=read(); pre(1,0); for(int i=1;i<=n;i++) dp[1]+=dep[i]*num[i]; dfs(1); for(int i=1;i<=n;i++) printf("%d ",dp[i]); printf(" "); } void getans(int x,int f) { ll ssum=0; for(int i=head[x];i;i=nxt[i]) { int y=to[i]; if(y==f)continue; getans(y,x); ssum+=sum[y]; } num[x]=sum[x]-ssum; } void solve() { for(int i=1;i<=n;i++) dp[i]=read(); DFS(1,0); ll total=0; for(int i=2;i<=n;i++) total+=1LL*dt[i]; sum[1]=1LL*(dp[1]*2+total)/(n-1); for(int i=2;i<=n;i++) sum[i]=(-dt[i]+sum[1])/2; getans(1,0); for(int i=1;i<=n;i++) printf("%d ",num[i]); printf(" "); } void ini() { for(int i=1;i<=n*2;i++) { to[i]=nxt[i]=0; if(i<=n)dp[i]=dt[i]=head[i]=sum[i]=num[i]=dep[i]=0; } tot=0; } void work() { n=read(); ini(); for(int i=1;i<n;i++) { int x=read(),y=read(); add(x,y);add(y,x); } op=read(); if(op)solve(); else cacl(); } int main() { T=read(); while(T--)work(); return 0; }
UPD:附赠两组样例

1 6 1 2 1 3 2 4 2 5 3 6 0 4 2 3 5 6 1 1 6 1 2 1 3 2 4 2 5 3 6 1 29 24 42 35 33 61
两组是对称的(一组输入为另一组输出)
