汉诺塔永远只有三步：
图中是最常见的五层(五珠)汉诺塔，其实几层都是一样，这里设为n，冰箱门永远是汉诺塔上面的m=n-1层。那么问题来了，怎样把冰箱门打开？即：怎样把图中的1至4号串珠从A柱移动到B柱？（三根柱子从左至右依次为A、B、C，五颗串珠从小到大依次为1到5）这又变成了一道m层汉诺塔的问题(m=n-1)。你可以继续用把大象装冰箱分几步的思路去考虑m层汉诺塔的解法。推导下去最终就得到了一个两层汉诺塔该怎么移动的问题，
关于汉诺塔的公式：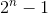
可以这样理解：
其中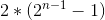
代表把冰箱门打开又合上，即完成两次n-1层汉诺塔的过程，
+1 代表移动汉诺塔最下面一层，即把大象装冰箱的过程。
冰箱门打开或者合上需要的步数都是一样的，
都是完成一个m=n-1层汉诺塔的过程。
----------------- 为什么 F(n) = 2 F(n-1) + 1，F(1) = 1 是最优的 -----------------
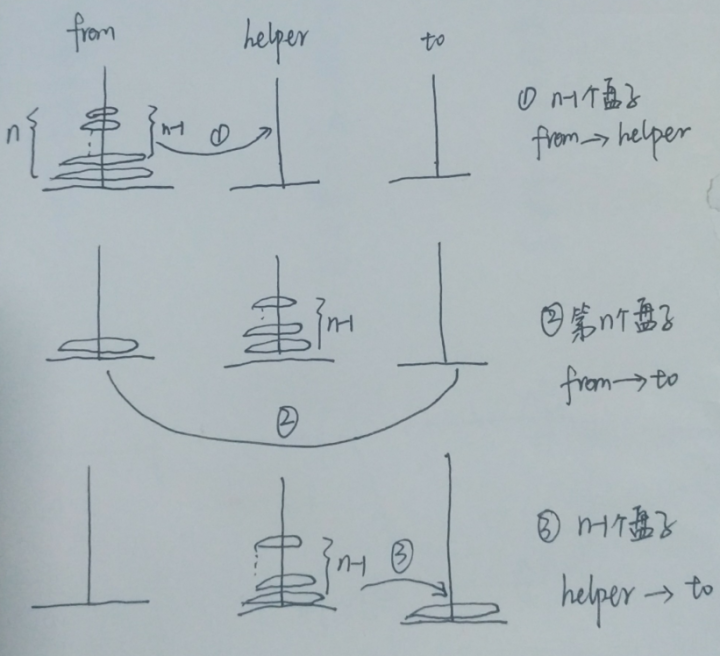
其实用数学归纳法就行了。最基本的情况，即n为1，就不用说了。
现在F(n-1)确实是把n-1个盘子集体挪动的最小步数，我们要证明F(n)是把n个盘子集体挪动的最小步数。
1）在把n个盘子从A移动到C的过程中，必然存在一步，是把最大的盘子从A拿出来。要想把最大的盘子从A移动到别的某个柱子上（B或C），就必须保证剩下的n-1个盘子不能碍事，得好好堆在剩下那个柱子（C或B）上。要保证n-1个盘子都在剩下那个柱子上，至少得付出F(n-1)次移动。
2）在把n个盘子从A移动到C的过程中，必然存在一步，是最大的盘子被放到了C上，而且此后再也没动过。在这步实行之前，最大的盘子要么在A要么在B上，而相应地别的n-1个盘子要么在B要么在A上。在这步实施之后，我们只要花至少F(n-1)的步数把n-1个盘子从要么B要么A挪动到C上就行了。这些步数必然和1）中的步数不重叠，因为这时候最大盘子在C上，而1）中最大盘子在A上。
3）最大的盘子至少被挪动了一次。而且这一次肯定没被算在1）或2）的“至少F(n-1)步”中，因为后者只挪动较小的那n-1个 盘子。
把1），2），3）加起来，就是至少F(n-1) + F(n-1) + 1步。不能再少了。