Even if the world is full of counterfeits, I still regard it as wonderful.
Pile up herbs and incense, and arise again from the flames and ashes of its predecessor — as is known to many, the phoenix does it like this.
The phoenix has a rather long lifespan, and reincarnates itself once every a! years. Here a! denotes the factorial of integer a, that is,a! = 1 × 2 × ... × a. Specifically, 0! = 1.
Koyomi doesn't care much about this, but before he gets into another mess with oddities, he is interested in the number of times the phoenix will reincarnate in a timespan of b! years, that is, 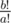 . Note that when b ≥ a this value is always integer.
. Note that when b ≥ a this value is always integer.
As the answer can be quite large, it would be enough for Koyomi just to know the last digit of the answer in decimal representation. And you're here to provide Koyomi with this knowledge.
The first and only line of input contains two space-separated integers a and b (0 ≤ a ≤ b ≤ 1018).
Output one line containing a single decimal digit — the last digit of the value that interests Koyomi.
2 4
2
0 10
0
107 109
2
In the first example, the last digit of 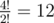 is 2;
is 2;
In the second example, the last digit of 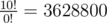 is 0;
is 0;
In the third example, the last digit of 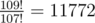 is 2.
is 2.
【题意】:如hint
【分析】:先化简 + 特判ans==0 + 因为只取最后一位每次可以%10防溢出
【代码】:

#include <bits/stdc++.h> using namespace std; int main() { long long a,b; long long ans;//Take care, integer overflow can emerge everywhere! while(~scanf("%lld%lld",&a,&b)) { ans=1; for(long long i=a+1;i<=b;i++) { ans=(ans*(i%10))%10; if(!ans) break; } printf("%lld ",ans); } return 0; } /*Hence we can multiply the integers one by one, only preserving the last digit (take it modulo 10 whenever possible), and stop when it becomes 0. It's obvious that at most 10 multiplications are needed before stopping, and it's not hard to prove a tighter upper bound of 5.*/
