在解上面这个问题前我们要先解决一个类似的问题:求字符串s的所有后缀和s本身的最长公共前缀;
我们用next[]数组保存这些值;
现在我们假设要求next[ x ],并且next[ i ] 0<i<x的值都已经求出;
我们设p = k + next[k] - 1, k是使p最大的 i (0<i<x);如图:

现在整理一下问题:
已知:s[k..p] == s[ 0 .. next[ k ]-1 ],求s[x .. n-1]与s[0 .. n-1]的最长公共前缀;
由s[k .. p] == s[ 0 .. next[ k ]-1 ] 得:
s[x .. p] == s[x-k .. next[ k ]-1 ] ---------1//这个是显然的
并设L1=p-x+1;
因为x-k肯定是小于x的所以 L2=next[x-k]是已知的,得:
s[0 .. L2-1] == s[x-k .. x-k+L2-1]; --------2
通过等式1,2可以推出 s[0 .. k1] == s[x .. k2]
if L1<=L2 then 如下图
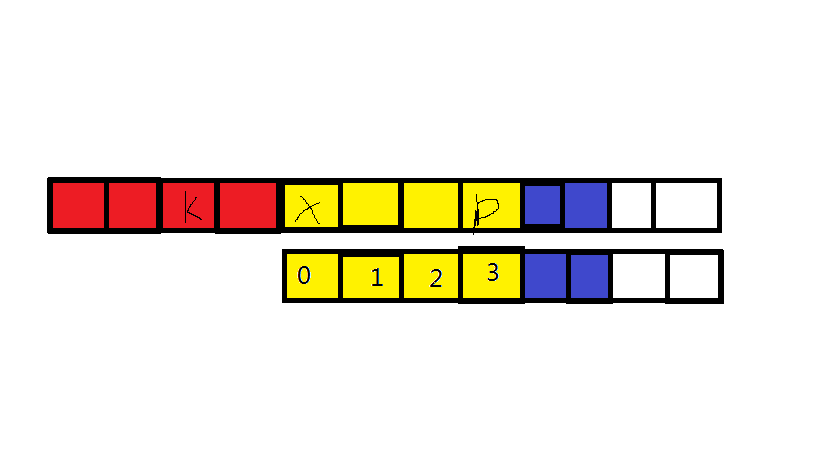
表示s[0 .. L1-1] == s[x .. x+L1-1]但不能确定蓝色部分是否相等,所以需要继续比下去
if L1 > L2 then 如下图:
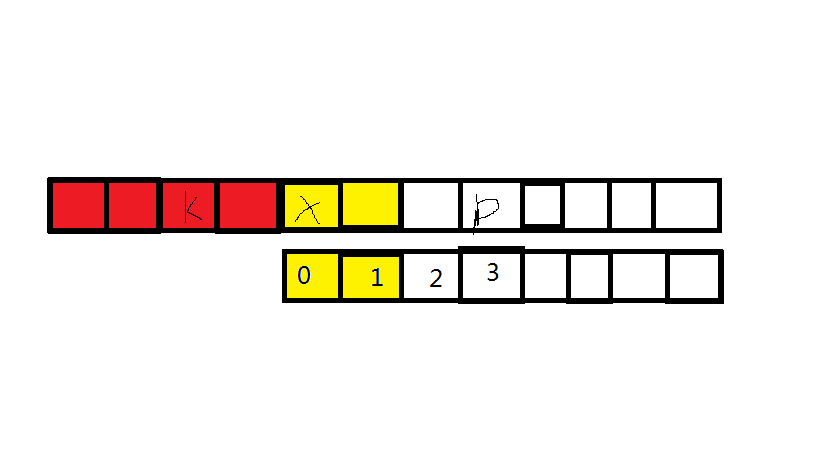
表示s[0 .. L2-1] == s[x .. x+L2-1] 而且因为L2 = next[x-k]使得s[L2] != s[x+L2]
所以next[x] = L2;
证明:假设s[L2]==s[x+L2],又因为s[x+L2]==s[x-k+L2]//由1推出
所以s[L2]==s[x-k+L2] 所以next[x-k]==L2+1与next[x-k]==L2矛盾
1 void getNext(char *s,int next[]){ 2 int nn = strlen(s); 3 next[0] = nn; 4 int p = 0; 5 while (p+1 < nn && s[p] == s[p+1]) p++; 6 next[1] = p; 7 int k = 1, L; 8 for (int i = 2; i < nn; i++){ 9 p = k + next[k] - 1; L = next[i - k]; 10 if (i + L <= p) next[i] = L; 11 else { 12 int j = p - i + 1; 13 if (j < 0) j = 0; 14 while (i + j < nn && s[i + j] == s[j]) j++; 15 next[i] = j; k = i; 16 17 } 18 } 19 /* for (int i=0;i<nn;i++){ 20 cout<< next[i] <<" "; 21 }cout<<endl; 22 */ 23 }
回到原来的问题
此时已经求出next[],我们用extend[]保存字符串S的所有后缀和字符串T的最长公共前缀的值
我们重复上面的过程:
现在我们假设要求extend[ x ],并且extend[ i ] 0<i<x的值都已经求出;
我们设p = k + extend[k] - 1, k是使p最大的 i (0<i<x);如图:

现在整理一下问题:
已知:s[k..p] == T[ 0 .. extend[ k ]-1 ],求s[x .. n-1]与T[0 .. m-1]的最长公共前缀;
由s[k .. p] == T[ 0 .. extend[ k ]-1 ] 得:
s[x .. p] == T[x-k .. extend[ k ]-1 ] ---------1//这个是显然的
并设L1=p-x+1;
因为x-k肯定是小于x的所以 L2=next[x-k]是已知的,得:
T[0 .. L2-1] == T[x-k .. x-k+L2-1]; --------2
通过等式1,2可以推出 T[0 .. k1] == s[x .. k2]
if L1<=L2 then 如下图

表示T[0 .. L1-1] == s[x .. x+L1-1]但不能确定蓝色部分是否相等,所以需要继续比下去
if L1 > L2 then 如下图:

表示T[0 .. L2-1] == s[x .. x+L2-1] 而且因为L2 = extend[x-k]使得T[L2] != s[x+L2]
所以extend[x] = L2;
证明:假设T[L2]==s[x+L2],又因为s[x+L2]==T[x-k+L2]//由1推出
所以T[L2]==s[x-k+L2] 所以extend[x-k]==L2+1与extend[x-k]==L2矛盾
1 void getExtend(char *s,char *T,int extend[]){ 2 int nn = strlen(s) ,mm = strlen(T); 3 getNext(s,next); 4 int p = 0; 5 while (p < nn && s[p] == T[p]) p++; 6 extend[0] = p; 7 //extend[1] = p; 8 int k = 0, L; 9 for (int i = 1; i < nn; i++){ 10 p = k + extend[k] - 1; L = next[i - k]; 11 if (i + L <= p) extend[i] = L; 12 else { 13 int j = p - i + 1; 14 if (j < 0) j = 0; 15 while (i + j < nn && s[i + j] == T[j]) j++; 16 extend[i] = j; k = i; 17 18 } 19 } 20 /* for (int i=0;i<nn;i++){ 21 cout<< extend[i] <<" "; 22 }cout<<endl; 23 */ 24 }
时间复杂度分析:
对于s串,每一位最多比较一次所以时间是O(n)的;