树的遍历非递归实现

树的非递归遍历

---

思路

---

观察如图的过程

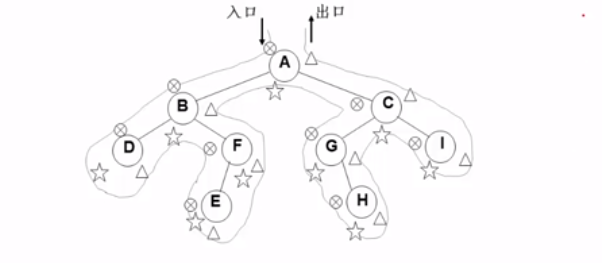
我们可以发现其实遍历的过程都是一样的,不一样是处理各个节点的时机

• 前序遍历是第一次访问到节点时处理节点
• 中序遍历是第二次访问到节点时处理节点
• 后序遍历是第三次访问到节点时处理节点

那么事情就变的简单了我们只要用栈来保存访问的节点即可,然后根据第几次访问来判断是否处理

---

代码

---

先序遍历

void preorder(tree t) {
  Node *p;
  stack<Node*> node_stack;
  if(t != NULL) {
    p = t;
    while(p || node_stack.size() != 0){
      if(p != NULL) {
	printf("%d
",p->data);         //第一次访问
	node_stack.push(p);
	p = p->left;
      }else {//此时节点为空将要访问栈顶元素的右节点
	p=node_stack.top();
	p = p->right;
	node_stack.pop();
      }
    }
  }
}

---

中序遍历

void inorder(tree t) {
  Node *p;
  stack<Node*> node_stack;
  if(t != NULL) {
    p = t;
    while(p || node_stack.size() != 0) {
      if(p != NULL) {
	node_stack.push(p);
	p = p->left;
      } else {
	p = node_stack.top();
	node_stack.pop();
	printf("%d
",p->data);    //p为空,此时栈顶元素为其父节点,进行第二次访问
	p = p->right;
      }
    }
  }
}

---

后序遍历

void postorder(tree t) {
  Node *p;
  stack<Node*> node_stack;
  map<Node*,int> times;
  if(t) {
    p = t;
    while(p || node_stack.size() != 0) {
      if(p != NULL) {
	node_stack.push(p);
	p = p -> left;
	continue;
      }
      p = node_stack.top();
      if(times.find(p) == times.end()) {
	times[p] = 1;
	p = p -> right;
      } else {
	node_stack.pop();
	printf("%d
",p -> data);
	p = NULL;    //必须设置不然栈顶又会被push一次    
      }
    }
  }
}

这一种思想就是上面的不过用一个hash表来判断是第几次访问
注意 p 必须设置为NULL不然会将栈顶元素再次push进来一次

---

void postorder(tree t) {
  stack<Node*> st;
  Node* pre=NULL;
  if(t) {
    st.push(t);
    while(!st.empty()) {
      t = st.top();
      if(((t->left == NULL) && (t->right == NULL))
	 ||
	 (pre != NULL)){
	printf("%d
",t->data);
	st.pop();
	pre = t;
      }else {
	if(t->right != NULL) st.push(t -> right);
	if(t->left != NULL) st.push(t->left);
      }
    }
  }
}

这一个思路和上面不同,考虑一个点如果它的左右子树为空则可以处理了
另一种可以处理该节点的情况就是两个子节点都访问过
否则将右子树先push进来然后将左子树push进来访问的时候就是按照左右根的顺序了

那么问题就是如何判断这两个子节点已经访问过了呢

直接用 pre != NULL 即可,它表示子节点不是两个都空时也可以处理该点
有些解法还加了 pre = t->left || pre = t->right,这是没有必要的,因为在压入的时候就已经保证该节点一定在该点子节点的下面
如果都访问该节点了,那么子节点都必然访问过了

---

相比于第一种解法,第二种应该还更优雅一点,而且它和层序遍历的队列实现法结构很像