单调栈
参考:
单调栈 - Shuyu Fang - CSDN博客
http://blog.csdn.net/alongela/article/details/8227707
单调栈的介绍以及一些基本性质 - 多反思,多回顾,要坚持。 - CSDN博客
http://blog.csdn.net/liujian20150808/article/details/50752861
单调栈poj2796 - 紫忆 - 博客园
http://www.cnblogs.com/ziyi--caolu/archive/2013/06/23/3151556.html
单调栈与单调队列很相似。首先栈是后进先出的,单调性指的是严格的递增或者递减。
单调栈有以下两个性质:
1、若是单调递增栈,则从栈顶到栈底的元素是严格递增的。若是单调递减栈,则从栈顶到栈底的元素是严格递减的。
2、越靠近栈顶的元素越后进栈。
单调栈与单调队列不同的地方在于栈只能在栈顶操作,因此一般在应用单调栈的地方不限定它的大小,否则会造成元素无法进栈。
元素进栈过程:对于单调递减栈,若当前进栈元素为e,从栈顶开始遍历元素,把小于e或者等于e的元素弹出栈,直接遇到一个大于e的元素或者栈为空为止,然后再把e压入栈中。对于单调递增栈,则每次弹出的是大于e或者等于e的元素。
一个单调递减栈的例子:
进栈元素分别为3,4,2,6,4,5,2,3
3进栈:(3)
3出栈,4进栈:(4)
2进栈:(4,2)
2出栈,4出栈,6进栈:(6)
4进栈:(6,4)
4出栈,5进栈:(6,5)
2进栈:(6,5,2)
2出栈,3进栈:(6,5,3)
以上左端为栈底,右端为栈顶。


一、单调栈的定义:
单调栈就是栈内元素单调递增或者单调递减的栈,单调栈只能在栈顶操作。
为了更好的理解单调栈,则可将单调栈用生活情形模拟实现,例如:
二、实例
我们借用拿号排队的场景来说明下。现在有很多人在排队买可乐,每个人手里都拿着号,越靠前的人手里的号越小,
但是号不一定是连续的。小明拿了号后并没有去排队,而是跑去约会了。等他回来后,发现队伍已经排得很长了,
他不能直接插入到队伍里,不然人家以为他是来插队的。小明只能跑到队伍最后,挨个询问排队人手里的号,
小明认为号比他大的人都是“插队”的,于是小明就会施魔法把这些人变消失,直到小明找到号比他小的为止。
在上面这个场景里,大家排的队伍就像是单调栈,因为大家手里拿的号是单调递增的。
而小明找自己位置的这个过程就是元素加入单调栈的过程。新加入的元素如果加到栈顶后,
如果栈里的元素不再是单调递增了,那么我们就删除加入前的栈顶元素,
就像小明施魔法把“插队”的人变消失一样。直到新元素加入后,栈依然是单调递增时,我们才把元素加进栈里。
(这样做的目的是“维护”单调栈,是单调栈保持原来的单调性不变)
三、从数组的角度阐述单调栈的性质:
给定一个包含若干个整数的数组,我们从第 1 个元素开始依次加入单调栈里,并且加入后更新单调栈。
那么单调栈有这样的性质:对于单调递增的栈,如果此时栈顶元素为 b,加入新元素 a 后进行更新时,
如果 a 大于 b,说明 a 在数组里不能再往左扩展了(由于单调栈的单调递增性质,b前面的元素均小于a),
也就是说,如果从 a 在数组中的位置开始往左边遍历,则 a 一定是第一个比 b 大的元素;
如果 a 小于 b,说明在数组里,a 前面至少有一个元素不能扩展到 a 的位置(至少有b元素,因为b的值要大于a,如果此时再加入新的
a,那么单调栈便不再单调,所以元素a此时不能压入栈顶,因为这并不是元素a"应该"在的位置,只有当元素a找到自己的位置时
元素a方能压入栈中,而这样做的前提是不改变单调栈的单调性),也就是对于这些元素来说,a 是其在数组右侧第一个比它小的元素。
单调栈的维护是 O(n) 级的时间复杂度,因为所有元素只会进入栈一次,并且出栈后再也不会进栈了。
四、单调栈的性质:
1.单调栈里的元素具有单调性
2.元素加入栈前,会在栈顶端把破坏栈单调性的元素都删除
3.使用单调栈可以找到元素向左遍历第一个比他小的元素,也可以找到元素向左遍历第一个比他大的元素。
对于第三条性质的解释(最常用的性质):
对于单调栈的第三条性质,你可能会产生疑问,为什么使用单调栈可以找到元素向左遍历第一个比他大的元素,
而不是最后一个比他大的元素呢?我们可以从单调栈中元素的单调性来解释这个问题,由于单调栈中的元素只能是单调递增或者是单调
递减的,所以我们可以分别讨论这两种情况(假设不存在两个相同的元素):
1.当单调栈中的元素是单调递增的时候,根据上面我们从数组的角度阐述单调栈的性质的叙述,可以得出:
(1).当a > b 时,则将元素a插入栈顶,新的栈顶则为a
(2).当a < b 时,则将从当前栈顶位置向前查找(边查找,栈顶元素边出栈),直到找到第一个比a小的数,停止查找,将元素a
插入栈顶(在当前找到的数之后,即此时元素a找到了自己的“位置”)
2.当单调栈中的元素是单调递减的时候,则有:
(1).当a < b 时,则将元素a插入栈顶,新的栈顶则为a
(2).当a > b 时,则将从当前栈顶位置向前查找(边查找,栈顶元素边出栈),直到找到第一个比a大的数,停止查找,将元素a
插入栈顶(在当前找到的数之后,即此时元素a找到了自己的“位置”)
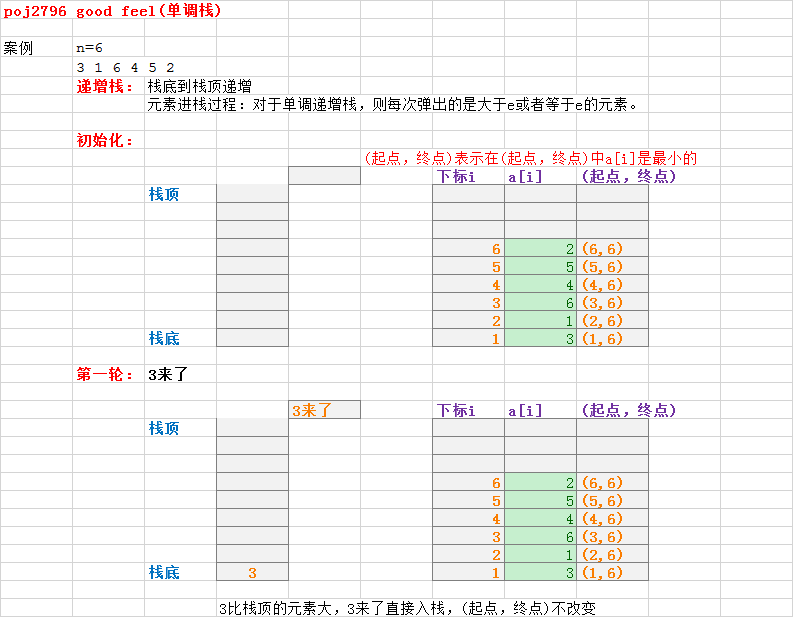
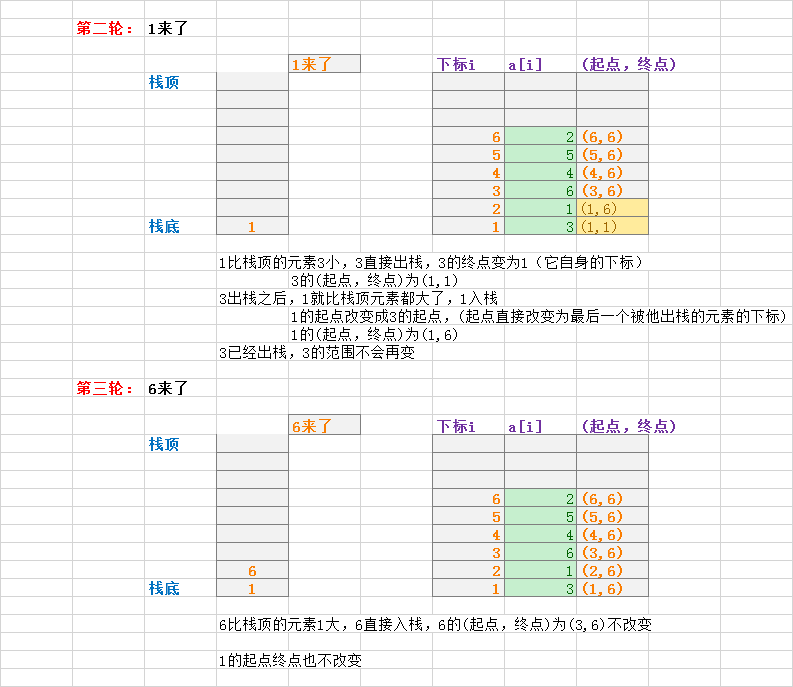
实例:poj2796
题目传送门:
2796 -- Feel Good
http://poj.org/problem?id=2796
| Time Limit: 3000MS | Memory Limit: 65536K | |
| Total Submissions: 15567 | Accepted: 4293 | |
| Case Time Limit: 1000MS | Special Judge |
Description
A new idea Bill has recently developed assigns a non-negative integer value to each day of human life.
Bill calls this value the emotional value of the day. The greater the emotional value is, the better the daywas. Bill suggests that the value of some period of human life is proportional to the sum of the emotional values of the days in the given period, multiplied by the smallest emotional value of the day in it. This schema reflects that good on average period can be greatly spoiled by one very bad day.
Now Bill is planning to investigate his own life and find the period of his life that had the greatest value. Help him to do so.
Input
Output
Sample Input
6 3 1 6 4 5 2
Sample Output
60 3 5
Source
题意:给你一段区间,在里面选一个小区间,需要你求出(在这段小区间之内的最小值*这段小区间所有元素之和)的最大值......
分析:
单调栈的原理,它就是以某一个值为最小(最大)值,向这个值的两侧延伸,遇到大于它(小于它)的值,就将它延伸的范围扩大,当然,一般来说,要这样做的算法复杂度为o(n^2),但是借助栈这个玩意,维护其单调增(减),就可以在o(n)的时间复杂度解决这个问题。
题目相当于是找每一个点,找以其为最小值的区间
显然直接暴力法找必然超时
可以开一个单调递增栈,
对于每一个新元素a[i]
当a[i]的值小于栈顶元素,表明栈顶元素的终点就是i-1(就是栈顶元素自身的下标),栈顶元素出栈,直到第一个比a[i]小的值,a[i]的起点就是被a[i]出栈的最后一个元素的下标。
当a[i]的值大于栈顶元素时,说明a[i]的起点为它自身,然后将a[i]入栈。
个人觉得其实可以把每个元素的终点都设置为n(最后一个元素的下标),因为当它出栈的时候,它的终点自然会被更新,不出栈说明终点为n,就不用修改了。它的起点被更新是在他入栈的时候。
初始化的时候,对于第i号元素将起点都设置为(i,n)。

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 using namespace std ; 5 const int maxn = 100010 ; 6 typedef __int64 ll ; 7 struct node 8 { 9 int l , r ; 10 ll num ; 11 }s[maxn] ; 12 ll a[maxn] ; 13 ll sum[maxn] ; 14 ll ans ; 15 int ans_l , ans_r ; 16 void update(int top) 17 { 18 int l = s[top].l , r = s[top].r ; 19 if((sum[r] - sum[l-1])*s[top].num > ans) 20 { 21 ans = (sum[r] - sum[l-1])*s[top].num ; 22 ans_l = l ; 23 ans_r = r ; 24 } 25 if(top > 0) 26 s[top-1].r = s[top].r ; 27 } 28 int main() 29 { 30 // freopen("in.txt","r" , stdin) ; 31 int n ; 32 while(~scanf("%d" , &n)) 33 { 34 ans = -1; 35 int top = -1 ; 36 sum[0] = 0 ; 37 for(int i = 1 ;i <= n ;i++) 38 { 39 scanf("%I64d" , &a[i]) ; 40 sum[i] = sum[i-1]+a[i] ; 41 } 42 for(int i = 1;i <= n;i++) 43 { 44 node v = {i , i ,a[i]}; 45 while(top != -1 && s[top].num >= a[i]) 46 { 47 update(top) ; 48 v.l = s[top].l ; 49 top-- ; 50 } 51 s[++top].l = v.l ; 52 s[top].r = v.r ; 53 s[top].num = v.num ; 54 } 55 while(top != -1) 56 { 57 update(top); 58 top-- ; 59 } 60 printf("%I64d " , ans) ; 61 printf("%d %d ",ans_l , ans_r) ; 62 } 63 return 0 ; 64 }