动态规划2--最长公共子序列
最长公共子序列1:http://www.cnblogs.com/Renyi-Fan/p/6955352.html
一、心得
所有的回溯找路径:记录之前来的路径
二、题目
找两个字符串的最长公共子序列
char s1[MAXLEN]={"ABCBDAB"};
char s2[MAXLEN]={"BDCABA"};
答案为4
三、分析
递推公式:
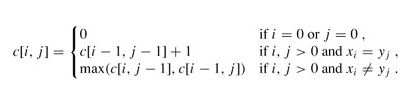
回溯路径:

四、代码及运行结果
1 /* 2 最长公共子序列2:回溯法求路径 3 所有的回溯找路径:记录之前来的路径 4 1、递推公式: 5 (分最后一个相同和最后一个不同来分析) 6 当i或j等于0,MaxLen(i,j)==0; 7 当s1和s2的最后一个字符相同时,MaxLen(i,j)=MaxLen(i-1,j-1)+1; 8 当s1和s2的最后一个字符不同时,MaxLen(i,j) = Max(MaxLen(i,j-1),MaxLen(i-1,j) ); 9 */ 10 /* 11 因为局部变量是在栈中的,所以像这样用函数传参数的话,数组不能太大 12 现在这里MAXLEN是100,可以,是1000的话就会出问题 13 解决方法:数组可以写成全局变量 14 */ 15 #include <iostream> 16 #include <cstring> 17 #define MAXLEN 100 18 using namespace std; 19 //求s1和s2的最长公共子序列 20 void LCSLength(char *s1,char *s2,int length1,int length2,int dp[][MAXLEN],int pre[][MAXLEN]){ 21 int i,j; 22 //初始化边界情况 23 for(i=0;i<=length1;i++) 24 dp[i][0]=0; 25 for(j=0;j<=length2;j++) 26 dp[0][j]=0; 27 for(i=1;i<=length1;i++){ 28 for(j=1;j<=length2;j++){ 29 if(s1[i-1]==s2[j-1]){//字符数组从0开始存数据的 30 //当s1和s2的最后一个字符相同时,dp(i,j)=dp(i-1,j-1)+1; 31 dp[i][j]=dp[i-1][j-1]+1; 32 pre[i][j]=0;//记录来的位置信息为0,表示从(i-1,j-1)位置而来 33 } 34 //当s1和s2的最后一个字符不同时,dp(i,j) = Max(dp(i,j-1),dp(i-1,j) ); 35 else if(dp[i-1][j]>=dp[i][j-1]){//比较(i-1,j)位置和(i,j-1)位置最长公共子序列的长度 36 dp[i][j]=dp[i-1][j]; 37 pre[i][j]=1;//记录来的位置信息为1,表示从(i-1,j)位置而来 38 } 39 else{ 40 dp[i][j]=dp[i][j-1]; 41 pre[i][j]=-1;//记录来的位置信息为-1,表示从(i,j-1)位置而来 42 } 43 } 44 45 } 46 } 47 //打印s1和s2的最长公共子序列 48 void PrintLCS(int pre[][MAXLEN],char *s1,int i,int j){ 49 if(i==0||j==0)//到达了边界 50 return ; 51 if(pre[i][j]==0){ 52 //查询记录来的位置信息为0,表示从(i-1,j-1)位置而来 53 PrintLCS(pre,s1,i-1,j-1); 54 //从(i-1,j-1)位置来表示字符相等,故打印 55 printf("%c",s1[i-1]); 56 } 57 else if(pre[i][j]==1){ 58 //查询记录来的位置信息为1,表示从(i-1,j)位置而来 59 PrintLCS(pre,s1,i-1,j); 60 } 61 else{ 62 //查询记录来的位置信息为-1,表示从(i,j-1)位置而来 63 PrintLCS(pre,s1,i,j-1); 64 } 65 } 66 67 int main(){ 68 char s1[MAXLEN]={"ABCBDAB"}; 69 char s2[MAXLEN]={"BDCABA"}; 70 /* 71 dp[MAXLEN][MAXLEN]表示进行动态规划运算的数组, 72 dp(i,j)表示s1的左边i个字符形成的子串, 73 与s2左边的j个字符形成的子串的最长公共子序列的长度(i,j从0开始算) 74 */ 75 int dp[MAXLEN][MAXLEN]; 76 //pre[i][j]用于记录ij位置的最长公共子序列是从哪个位置推导出来的 77 int pre[MAXLEN][MAXLEN]; 78 int length1=strlen(s1);//求字符数组s1的长度 79 int length2=strlen(s2);//求字符数组s2的长度 80 LCSLength(s1,s2,length1,length2,dp,pre);//求s1和s2的最长公共子序列 81 cout<<dp[length1][length2]<<endl; //输出s1和s2的最长公共子序列的长度 82 PrintLCS(pre,s1,length1,length2);//打印s1和s2的最长公共子序列 83 cout<<endl; 84 return 0; 85 }
