动态规划1--最长公共子序列

动态规划1--最长公共子序列

一、动态规划

经常会遇到复杂问题不能简单地分解成几个子问题，而会分解出一系列的子问题。简单地采用把大问题分解成子问题，并
综合子问题的解导出大问题的解的方法，问题求解耗时会按问题规模呈幂级数增加。

为了节约重复求相同子问题的时间，引入一个数组，不管它们是否对最终解有用，把所有子问题的解存于该数组中，这就
是动态规划法所采用的基本方法。

二、心得

递推公式的推导

递推公式的证明方法

代码的写法：把递推公式直接写进代码即可

三、题目

给出两个字符串，求出这样的一个最长的公共子序列的长度：子序列中的每个字符都能在两个原串中找到，而且每个字符的先后顺序和原串中的先后顺序一致。

Sample Input：样例输入

abcfbc abfcab

programming contest

abcd mnp

Sample Output：样例输出

4
2
0

四、分析

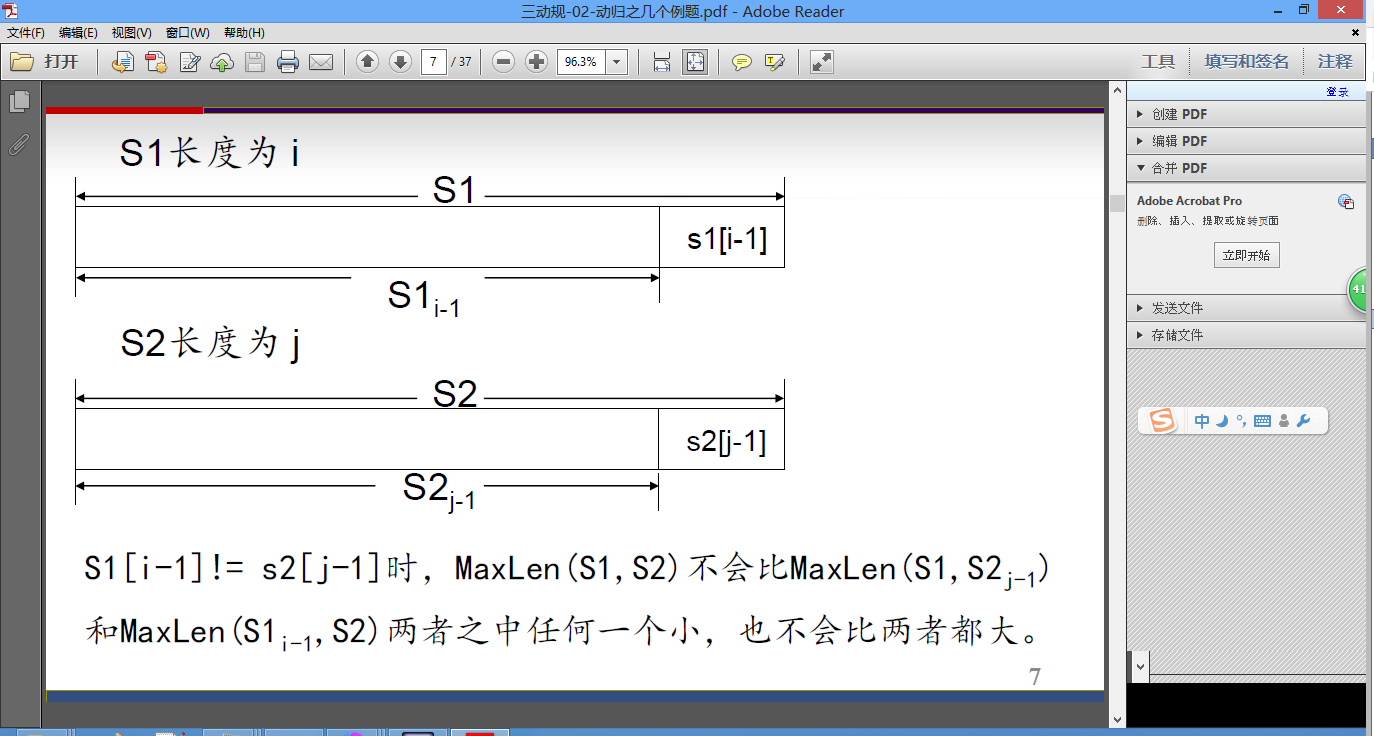
2、证明
S1[i-1]!= s2[j-1]时，MaxLen(S1,S2)不会比MaxLen(S1,S2j-1)
和MaxLen(S1i-1,S2)两者之中任何一个小，也不会比两者都大。
（1）不比任何一个小：MaxLen(S1,S2)字符串长于后两者
（2）也不会比两者都大：反证法，假设比两者都大：

若MaxLen(S1,S2)比MaxLen(S1,S2j-1)大，说明S2(j)这个字符与S1中的字符相等，并且S2(j)和这个相等的字符是最长公共子序列的最后一个。

若MaxLen(S1,S2)比MaxLen(S1i-1,S2)大，说明S1(i)这个字符与S2中的字符相等，并且S1(i)和这个相等的字符是最长公共子序列的最后一个。

上面两种情况都是最长公共子序列的最后一个，而这个最长公共子序列是MaxLen(S1,S2)的最长公共子序列，所以最后一个要相等。

那会得出S1[i]== s2[j]的结论，与假设冲突。

五、代码及结果

/*
最长公共子序列 
1、递推公式：
（分最后一个相同和最后一个不同来分析） 
当i或j等于0，MaxLen(i,j)==0;
当s1和s2的最后一个字符相同时，MaxLen(i,j)=MaxLen(i-1,j-1)+1;
当s1和s2的最后一个字符不同时，MaxLen(i,j) = Max(MaxLen(i,j-1),MaxLen(i-1,j) ); 
2、证明 
S1[i-1]!= s2[j-1]时，MaxLen(S1,S2)不会比MaxLen(S1,S2j-1)
和MaxLen(S1i-1,S2)两者之中任何一个小，也不会比两者都大。
（1）不比任何一个小：MaxLen(S1,S2)字符串长于后两者
（2）也不会比两者都大：反证法，假设比两者都大，那会得出S1[i-1]== s2[j-1]的结论，与假设冲突 
3、代码
直接写递推公式就好了 
*/
/*
错误一：结果不对
for(j=1;j<=length2;j++)，漏了等号，所以都没执行到这来，所以结果不对 
*/
#include <iostream>
#include <cstring> 
using namespace std;
char sz1[1000];//字符数组1 
char sz2[1000];//字符数组2 
int maxLen[1000][1000];
//MaxLen(i,j)表示s1的左边i个字符形成的子串，
//与s2左边的j个字符形成的子串的最长公共子序列的长度(i,j从0开始算） 
int main(){
    freopen("in.txt","r",stdin); 
    while(cin>>sz1>>sz2){
        int length1=strlen(sz1);//求字符数组1的长度 
        int length2=strlen(sz2);//求字符数组2的长度
        int nTmp;
        int i,j;
        //初始化边界情况 
        for(i=0;i<=length1;i++)
            maxLen[i][0]=0;
        for(j=0;j<=length2;j++)
            maxLen[0][j]=0; 
        //动态规划求解最长公共子序列  
        for(i=1;i<=length1;i++){
            for(j=1;j<=length2;j++){
                if(sz1[i-1]==sz2[j-1]){//字符数组从0开始存数据的 
                    //当s1和s2的最后一个字符相同时，MaxLen(i,j)=MaxLen(i-1,j-1)+1; 
                    maxLen[i][j]=maxLen[i-1][j-1]+1;
                }    
                else{
                    //当s1和s2的最后一个字符不同时，MaxLen(i,j) = Max(MaxLen(i,j-1),MaxLen(i-1,j) );  
                     maxLen[i][j]=max(maxLen[i][j-1],maxLen[i-1][j]);
                }
            } 
                        
        }
        /*
        for(i=1;i<=length1;i++){
            for(j=1;j<=length2;j++){
                cout<<maxLen[i][j]<<" ";
            }
            cout<<endl;
        }
        */ 
        //cout<<length1<<" "<<length2<<endl;
        cout<<maxLen[length1][length2]<<endl;
    }
    return 0;
}