卷积基本定义

卷积基本定义

一、总结

一句话总结：

A、【两个函数f 和g 生成第三个函数】：卷积(英语：Convolution)是通过两个函数f 和g 生成第三个函数的一种数学算子

B、【重叠部分函数值乘积对重叠长度的积分】：函数f 与g经过翻转和平移的重叠部分函数值乘积对重叠长度的积分

C、卷积公式：$$int _ { - infty } ^ { infty } f ( au ) g ( x - au ) d au$$

在泛函分析中，卷积(英语：Convolution)是通过两个函数f 和g 生成第三个函数的一种数学算子，表征函数f 与g经过翻转和平移的重叠部分函数值乘积对重叠长度的积分。

二、卷积基本定义

转自或参考：卷积_百度百科
https://baike.baidu.com/item/%E5%8D%B7%E7%A7%AF/9411006?fr=aladdin

在泛函分析中，卷积、旋积或摺积(英语：Convolution)是通过两个函数f 和g 生成第三个函数的一种数学算子，表征函数f 与g经过翻转和平移的重叠部分函数值乘积对重叠长度的积分。

简单定义：卷积是分析数学中一种重要的运算。

设:f(x),g(x)是R1上的两个可积函数，作积分：

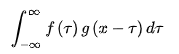
可以证明，关于几乎所有的实数x，上述积分是存在的。这样，随着x的不同取值，这个积分就定义了一个新函数h(x)，称为函数f与g的卷积，记为h(x)=(f*g)(x)。

容易验证，(f * g)(x) = (g * f)(x)，并且(f * g)(x)仍为可积函数。这就是说，把卷积代替乘法，L1（R1）空间是一个代数，甚至是巴拿赫代数。

卷积与傅里叶变换有着密切的关系。利用一点性质，即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换，能使傅里叶分析中许多问题的处理得到简化。

由卷积得到的函数f*g一般要比f和g都光滑。特别当g为具有紧致集的光滑函数，f为局部可积时，它们的卷积f * g也是光滑函数。利用这一性质，对于任意的可积函数f，都可以简单地构造出一列逼近于f的光滑函数列fs，这种方法称为函数的光滑化或正则化。

卷积的概念还可以推广到数列、测度以及广义函数上去。