softmax与多分类
一、总结
一句话总结：
sotfmax 函数在机器学习和深度学习中有着广泛的应用， 主要用于多分类问题。
1、softmax 函数 定义？
A、Si=e^(Vi)/(Σe^(Vj))
B、也就是该元素的指数 除以 所有元素的指数和，取指数是为了使差别更大。
C、于是该数组的每个元素被压缩到(0,1)，并且和为1，其实就变成了概率。
D、在多分类问题中代表了该元素被取到的概率。
2、softmax 感性理解？
1、softmax可以拆开来看，一个soft，一个max，max顾名思义取最大值，数组中哪个元素最大，一定取到哪个，
2、然而当数组被softmax之后，变成了概率，被用来代表元素被取到的概率，那么最大的最容易被取到，而不是一定被取到，这就是soft。
3、其实就是强化学习中的探索率。
二、softmax与多分类
转自或参考：softmax与多分类
https://www.cnblogs.com/yanshw/p/10443735.html
sotfmax 函数在机器学习和深度学习中有着广泛的应用， 主要用于多分类问题。
softmax 函数
1. 定义
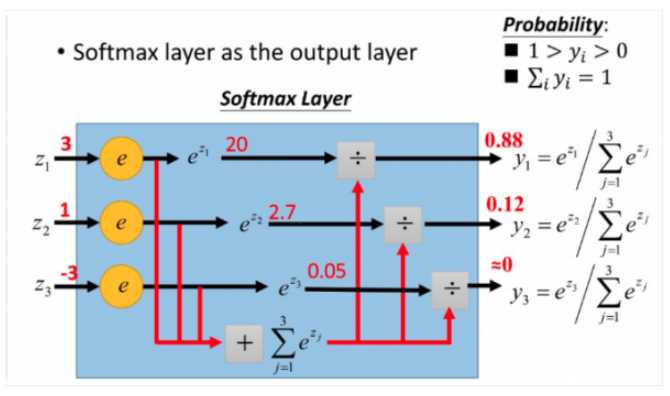
假定数组V，那么第i个元素的softmax值为
也就是该元素的指数 除以 所有元素的指数和，取指数是为了使差别更大。
于是该数组的每个元素被压缩到(0,1)，并且和为1，其实就变成了概率。在多分类问题中代表了该元素被取到的概率。
例如
2. 感性理解
softmax可以拆开来看，一个soft，一个max，max顾名思义取最大值，数组中哪个元素最大，一定取到哪个，
然而当数组被softmax之后，变成了概率，被用来代表元素被取到的概率，那么最大的最容易被取到，而不是一定被取到，这就是soft。
其实就是强化学习中的探索率。
多分类的问题
1. one-hot vector
多分类的目标值通常用one-hot vector表示，为什么呢？
假定有100个类别，我们设定类别标号为1-100，有一个样本真实标签为100，而预测为1，你能说他们的差是99吗？还有一个样本真实标签50，预测40，你能说预测的更准吗？显然不合理。
2. 详解 softmax 解决多分类问题
假定有m个样本，即[x1,x2,...xm]，每个样本n个属性，即xi=[a1,a2,...an]，共分为k类，yi=[0,0,...1...0]，第i个位置是1，其余是0。
每类的概率Pk=P(y(k)=1)，且ΣΡ=1。
用另一种方式来表示Pk=1{y=k}Pk
现在我们来模拟多分类过程：
首先需要搞清楚一点：分类是干啥的，输入一个样本x，看看他属于哪一类，输出是一个向量y’，表示该样本属于每一类的概率，假设y'=[1/2,1/4,1/4]， 真实类别y=[0,1,0]
然后我们怎么办呢？此处开始划重点。
咋一想，取最大的那个概率，但是然后呢？这里最大概率对应的类别是1，而实际类别是2，貌似没办法往下走了，
再仔细想想，应该取真实类别对应的那个概率1/4，而且我们希望这个概率就是最大的，
这里其实可以用最小二乘的思路，真实的类别y肯定是1（真实概率），那么真实类别y中1的位置对应的输出y’的位置的概率1/4就是我们的预测值，预测值与真实值的差就是loss，
当然我们这里采用极大似然的思路，就是让这个概率最大，即预测尽量接近真实，（其实在这里最小二乘和极大似然是一个意思，最小二乘是减小loss，1-p，而极大似然就是让p尽量大，最大是1）
接着再取一个样本，就是2个样本，我们希望这两个样本的预测尽量接近真实，那么就是两个样本的概率相乘，然后尽量大，
n个样本呢，n个概率相乘，使这个乘积最大，这就是代价函数。
把上述过程用数学公式来表示
设m个样本，共k个类，yi € {1,2,3...k}，每个样本预测到的概率为P，P为一个向量，长度为k
那么每个样本从Pt中取到的值是
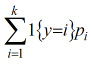
y为真实类别，当y=i时，1{y=i}为1，否则为0，Pi为预测值的第i个元素，上式的意思是当y=i时，取此时的Pi，实际上就是一个数值，求和只是唬人的。
那么m个样本对应的代价函数是
yj是第j个样本的真实标签，pj是第j个样本的输出
然后使代价函数最大，先取log，在加负号，即求最小，除以m好求导
这样取log貌似不太好理解，可以这样想，
其实这是一个循环，for j=1：m
在j给定时，Σ1{yj=i}Pj其实是一个数，这个数就是Pj中的某个，然后我们用1{}把这个数取到就行了。
另一种表示方式更容易理解
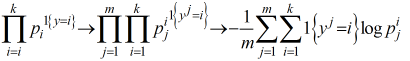
然后求偏导，令导数等于0，梯度下降
那么，Pj是多少？此时就用到softmax了。
wx+b得到的是个数值，不是概率，这时需要用softmax转换成概率。
这个式子表示样本x被分为第j类的概率。这个Pj不是我们上面公式里的Pj，这里的Pj是一个数，公式里的是一个向量。
插曲 ---- 细心的人会发现两个问题：
1. 分子上θ的下标是j，而j是类别，不是应该是样本的属性个数吗？ θiXi
2. 分母上求和用的l，l和j都表示类别，这里要区分开。
那么第一个问题怎么解释？
多分类里的θ比较特殊，是一个矩阵，而逻辑回归是个向量，因为多分类相当于是多个分类器，每个分类器有自己的模板，所以该矩阵大小为 类别数X属性数
（图是盗的，T表示属性个数，k类别个数，每行代表一个类别的模板，就是上面公式中的θj）
回到正题----下面的部分网上都有，所以盗图了，我会备注盗图，有些字母跟上文不太一样，我会稍加说明。
经过softmax转换，代价函数表示为
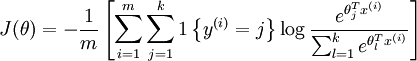
（盗图，这里i表示样本数，j表示类别数，T表示属性数）
然后就是求偏导了
首先要明确一点：
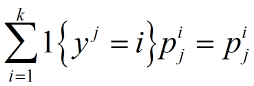这点比较重要
我的求导
写的有些乱，看网上的吧
然后梯度下降。
softmax 参数冗余
有空再说
softmax 权重衰减
权重衰减可以解决参数冗余问题。
其实就是正则化，有空再说
softmax VS k个二分类
多分类和k个二分类哪个更好？如何选择？取决于事物的类别是否互斥。
比如篮球、足球、台球，一个球只能属于3种中的一种，或者你可以增设一个其他球，一个球只能属于4种中的一种，此时用softmax多分类
比如流行歌曲、摇滚歌曲、港台歌曲，一首歌可以属于流行，同时也可以属于摇滚，此时用多个二分类，分别判断是不是流行，是不是摇滚，是不是港台。
softmax 与 交叉熵
交叉熵的公式为 loss=-Σtv*log(pv) true_value代表真实值，predict_value代表预测值。
让我们再回想一下上面softmax多分类的代价函数
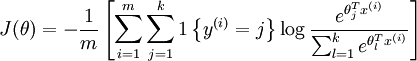
log左边是真实标签，右边是预测标签，这不就是交叉熵吗？
所以softmax多分类用交叉熵作为代价函数。
在分类问题中，交叉熵函数已经大范围的代替了均方误差函数。
也就是说，在输出为概率分布的情况下，就可以使用交叉熵函数作为理想与现实的度量。
这也就是为什么它可以作为有 Softmax 函数激活的神经网络的损失函数。
softmax 与 sigmoid 的关系
有空再说