首先交代下背景,课题需要产生服从高斯分布的随机变量,这个要求对于python,Matlab而言,也就是一个函数调用的事(其实C++的库里面也有,无奈之前不知道,(⊙o⊙)…),假如不调用,我们自己应当如何实现呢?或者再延伸下,如果我们需要产生任意分布,这下没函数调用了吧,那么我们应该怎么办呢?这就是一个比较有意思的问题了......
首先来看看我们有啥可以用的,一般而言我们是可以获取随机数的(其实这个随机数也是伪随机数,可以通过线性同余法来产生,这是后话了),我们可以把这个数看做服从均匀分布的随机变量,那么如何将一个均匀分布的变量映射到另一个分布的变量呢?
答案如下:

x为均匀分布的变量,y为另一分布的变量,利用其累计函数作为中间关系,来完成映射。那么问题又来了,为什么可以这样呢?如何来理解这一问题呢?
来两张图感性认识下:
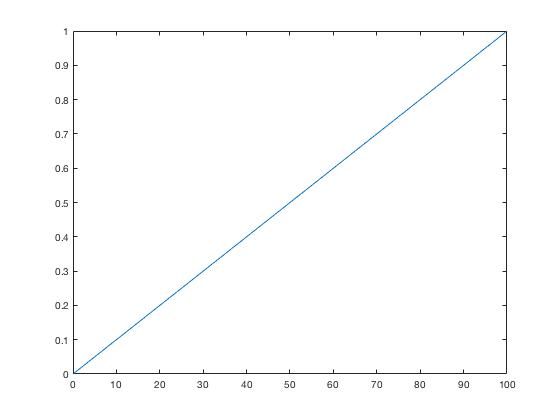

前者是0到100的均匀分布累计函数,后者是N(50,25)的累计函数,可以发现:
1.二者均为递增函数(可以看做严格单调,尽管不明显)
2.函数值范围为[0,1]
映射的原理就是在由均匀分布变量的值找到其累计函数值,对应到图二中相同函数值所对应变量值,由上面两幅图可以发现,图一中几乎所有值都对应到了图二中的40~60中,这在直观上和正态分布的效果是相符的。
接下来就看看如何来程序实现,
//---------------------GaussianDistribution.h------------------------
#pragma once
//#include "Interface.h"
#define SP 1000//设置精确度,取整个正态分布的区间分为SP等份
namespace RAN
{
class GaussianDistribution {
public:
GaussianDistribution(void);
~GaussianDistribution(void);
double u,d,step;
double mp[SP],mf[SP];//mp为正态分布区间每等份所对应的概率密度,mf为累计累计概率密度
void SetPara(double u,double d);
double GetOne();
};
}
//---------------------GaussianDistribution.cpp------------------------
#include "GaussianDistribution.h"
#include <cmath>
#define PI 3.1415926
#include <time.h>
GaussianDistribution::GaussianDistribution(void)
{
}
GaussianDistribution::~GaussianDistribution(void)
{
}
template<typename T>
int BinarySearch(T *array,T key)//二分查找,返回值所在数组中的位置,若无则返回其左边值
{
int aSize=SP;
if ( array == NULL || aSize == 0 )
return -1;
int low = 0;
int high = aSize - 1;
int mid = 0;
while ( low <= high )
{
mid = (low + high )/2;
if ( array[mid] < key)
low = mid + 1;
else if ( array[mid] > key )
high = mid - 1;
else
return mid;
}
return low;
}
void GaussianDistribution::SetPara(double u,double d)
{
this->u=u;
this->d=d;
step=10*d/SP;//取正态分布整个区间中以u为中心,5d为半径的区间
mf[0]=0;
mp[0]=0;
for (int i=1;i<SP;i++)
{
double x=u+(step*(i-SP/2));//计算pdf中的x值
mp[i]=1/(sqrt(2*PI)*d)*exp(-(x-u)*(x-u)/(2*d*d));//x对应概率密度
mf[i]=mf[i-1]+mp[i]*step;//累计概率密度
}
srand(time(0));
}
double GaussianDistribution::GetOne()
{
//srand(time(0)); //use current time as seed for random generator
int random= rand();
double p= (random+0.0)/RAND_MAX;//均匀分布累计概率密度
int k=BinarySearch(mf,p);//找到正态分布的对应
double gg=u+(k-SP/2)*step;
return gg;
}