jzoj3573. 【GDKOI2014】逃出生天

Description

Sample Input

输入1：

3 3 2
...

...

...

输入2：

4 5 2
..*..

*....

.*...

.....

Sample Output

输出1：

6

输出2：

1

Data Constraint

题解

这题的想法是真滴妙♂
首先30分还是比较简单地可以拿到的。

看到100分。
第一步考虑一个简单的问题，给定一个(k*k)的矩阵，从((1,1))开始走，走k步之后走到某个位置且不越界，不碰障碍的方案数为多少个。
这是一个简单dp，由于k比较小，所以可以随便设状态或跑bfs。
设(dis[k][i][j])表示走了k步，走到((i,j))的方案数。

现在已经解决这个小问题了。由于飞船的行驶是周期性的，也就是说，每走k步达到的终点，可以看做是在一个新地图上再走k步。
那么就考虑把整个地图浓缩在同一个(k*k)的地图中，那么走一遍就可以得到答案了。

更好的理解可以看下面题解给的图片：


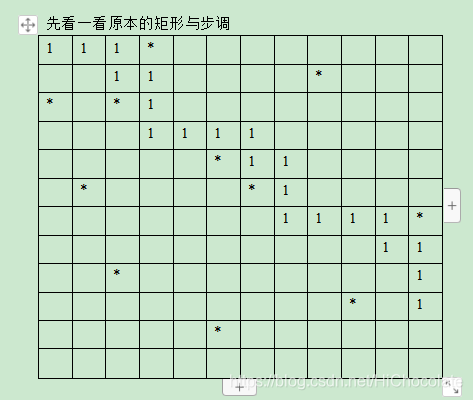
压缩之后：

代码

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
using namespace std;
const long long mo=1e8+7;
const int maxn=210;

int fx[4][2]={{-1,0},{1,0},{0,1},{0,-1}};
int n,m,k,ma[maxn][maxn],bz[maxn][maxn];
long long dis[maxn][50][50],ans;
char s[maxn];

void dfs(int st,int en)
{
	memset(bz,0,sizeof(bz));
	for (int i=0;i<=100;i++)
	{
		if ((st-1)*i+1>n || (en-1)*i+1>m) break;
		for (int x=1;x<=k+1;x++)
		{
			for (int y=1;y<=k+1;y++)
			{
				bz[x][y]=bz[x][y]|ma[x+i*(st-1)][y+i*(en-1)];
				
			}
		}
	}
	if (bz[1][1]==1) return;
	else
	{
		memset(dis,0,sizeof(dis));
		dis[0][1][1]=1;
		for (int i=0;i<k;i++)
		{
			for (int x=1;x<=k+1;x++)
			{
				for (int y=1;y<=k+1;y++)
				{
					if (dis[i][x][y]>0)
					{
						for (int j=0;j<=3;j++)
						{
							int xx=x+fx[j][0];
							int yy=y+fx[j][1];
							if (xx>0 && xx<=k+1 && yy>0 && yy<=k+1 && bz[xx][yy]==0)
							{
								dis[i+1][xx][yy]=(dis[i+1][xx][yy]+dis[i][x][y])%mo;
							}
						}
					}
				}
			}
		}
		for (int i=1;i<=k;i++)
		{
			ans=(ans+dis[i][st][en])%mo;
		}
	}
}

int main()
{
	scanf("%d%d%d",&n,&m,&k);
	for (int i=1;i<=n;i++)
	{
		scanf("%s",s+1);
		for (int j=1;j<=m;j++)
		{
			if (s[j]=='*') 
			{
				ma[i][j]=1;
			}
		}
	}
	for (int i=1;i<=k+1;i++)
	{
		for (int j=1;j<=k+1;j++)
		{
			if (i+j<=k+2 && ma[i][j]==0)
			{
				if (i==1 && j==1) continue;
				dfs(i,j);
//				printf("%d %d %d
",i,j,ans);
			}
		}
	}
	printf("%d
",ans);
}